Bài 53 trang 102 SGK Toán 7 tập 1
Cho định lí: " Nếu hai đường thẳng xx', yy' cắt nhau tại O góc xOy vuông thì các góc yOx', x'Oy', y'Ox đều là góc vuông".
Đề bài
Cho định lí: " Nếu hai đường thẳng \(xx', yy'\) cắt nhau tại \(O\) và góc \(xOy\) vuông thì các góc \(yOx', x'Oy', y'Ox\) đều là góc vuông".
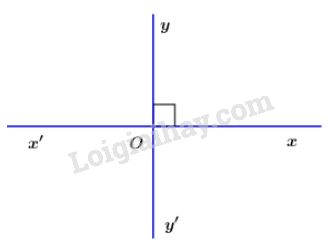
a) Hãy vẽ hình.
b) Viết giả thiết và kết luận định lí.
c) Điền vào chỗ trống (...) trong các câu sau:
1) \(\widehat{xOy} + \widehat{x'Oy} = {180^o}\) (Vì ...).
2) \({90^o}+\widehat{x'Oy} = {180^o}\) (theo giả thiết và căn cứ vào ...).
3) \(\widehat{x'Oy}={90^o}\) (căn cứ vào ...).
4) \(\widehat{x'Oy'} = \widehat{xOy}\) (Vì ...).
5) \(\widehat{x'Oy'}={90^o}\) (căn cứ vào).
6) \(\widehat{y'Ox} = \widehat{x'Oy}\) (vì ...).
7) \(\widehat{y'Ox}={90^o}\) (căn cứ vào ...).
d) Hãy trình bày lại chứng minh một cách ngắn gọn hơn.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề bù có tổng bằng \(180^0.\)
Lời giải chi tiết
a) Vẽ
b)
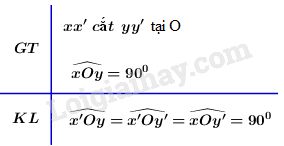
c)
1) \(\widehat{xOy} + \widehat{x'Oy} = {180^o}\) (vì là hai góc kề bù).
2) \({90^o}+\widehat{x'Oy} = {180^o}\) (theo giả thiết và căn cứ vào 1).
3) \(\widehat{x'Oy}={90^o}\) (căn cứ vào 2).
4) \(\widehat{x'Oy'} = \widehat{xOy}\) (vì là hai góc đối đỉnh).
5) \(\widehat{x'Oy'}={90^o}\) (căn cứ vào 4 và giả thiết).
6) \(\widehat{y'Ox} = \widehat{x'Oy}\) (vì là hai góc đối đỉnh).
7) \(\widehat{y'Ox}={90^o}\) (căn cứ vào 6 và 3).
d) Trình bày lại cách chứng minh một cách gọn hơn.
Ta có: \(\widehat{xOy} + \widehat{x'Oy}=180^o\) (hai góc kề bù)
Mà \(\widehat{xOy}={90^o}\) (gt) nên \({90^o}+\widehat{x'Oy}={180^o}\)
\( \Rightarrow \widehat{x'Oy}=180^o-90^o={90^o}\)
\(\widehat{x'Oy} = \widehat{xOy'}\) (hai góc đối đỉnh).
\( \Rightarrow \widehat{y'Ox}={90^o}\)
\(\widehat{x'Oy'} = \widehat{xOy}\) (hai góc đối đỉnh).
\( \Rightarrow \widehat{x'Oy'}={90^o}\)
Loigiaihay.com













Danh sách bình luận