-
Đề kiểm tra 15 phút
-
Đề kiểm tra 15 phút - Chương I - Giải Tích 12
-
Đề kiểm tra 15 phút - Chương II - Giải Tích 12
-
Đề kiểm tra 15 phút - Chương III - Giải Tích 12
-
Đề kiểm tra 15 phút – Chương IV – Giải tích 12
-
Đề kiểm tra 15 phút - Chương I - Hình học 12
-
Đề kiểm tra 15 phút - Chương II - Hình học 12
-
Đề kiểm tra 15 phút - Chương III - Hình học 12
-
-
Đề kiểm tra 1 tiết
-
Đề kiểm tra 45 phút (1 tiết) - Chương I - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương II - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương III - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương IV - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương I - Hình học 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương II - Hình học 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương III - Hình học 12
-
-
Đề thi giữa học kì 1
-
Đề thi học kì 1
-
Đề thi giữa học kì 2
-
Đề thi học kì 2
-
ĐỀ THI THỬ THPT QUỐC GIA MÔN TOÁN
Đề kiểm tra 15 phút Toán 12 chương 2: Hàm số lũy thừa, mũ, logarit - Đề số 3
Đề bài
Tổng các nghiệm của phương trình \({3^{{x^4} - 3{x^2}}} = 81\)
-
A.
$0$
-
B.
$1$
-
C.
$3$
-
D.
$4$
Tập xác định của hàm số \(f\left( x \right) = \sqrt {{{\log }_{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}}} \) là:
-
A.
\(D = \left( { - \infty ;\dfrac{{ - 3 - \sqrt {17} }}{2}} \right] \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2}; + \infty } \right)\)
-
B.
\(D = \left( { - \infty ; - 3} \right) \cup \left( {1; + \infty } \right)\)
-
C.
\(D = \left( {\dfrac{{ - 3 - \sqrt {17} }}{2}; - 3} \right) \cup \left( {\dfrac{{ - 3 + \sqrt {17} }}{2};1} \right)\)
-
D.
\(D = \left[ {\dfrac{{ - 3 - \sqrt {17} }}{2}; - 3} \right) \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2};1} \right)\)
Cho x>0; \(x \ne 1\) thỏa mãn biểu thức $\dfrac{1}{{{{\log }_2}x}} + \dfrac{1}{{{{\log }_3}x}} + ... + \dfrac{1}{{{{\log }_{2017}}x}} = M$ . Khi đó $x$ bằng:
-
A.
\(x = \sqrt[M]{{2017!}} - 1\)
-
B.
\(x = \sqrt[M]{{2018!}}\)
-
C.
\(x = \sqrt[M]{{2016!}}\)
-
D.
\(x = \sqrt[M]{{2017!}}\)
Tập nghiệm của bất phương trình \({\left( {2 + \sqrt 3 } \right)^{\dfrac{{x - 3}}{{x - 1}}}} < {\left( {2 - \sqrt 3 } \right)^{\dfrac{{x - 1}}{{x - 3}}}}\) là :
-
A.
\(1 - \sqrt 3 \le x \le 0\)
-
B.
\(2 \le x \le 1 + \sqrt 3 \)
-
C.
\(1 - \sqrt 3 \le x \le 0 \cup 2 \le x \le 1 + \sqrt 3 \)
-
D.
\(1 - \sqrt 3 \le x \le 0 \cap 2 \le x \le 1 + \sqrt 3 \)
Phương trình \({4^{2x + 5}} = {2^{2 - x}}\) có nghiệm là:
-
A.
\(\dfrac{{ - 8}}{5}\)
-
B.
\(3\)
-
C.
\(\dfrac{8}{5}\)
-
D.
\(\dfrac{{12}}{5}\)
Cho phương trình ${\log _2}\left[ {{{\log }_{\dfrac{1}{8}}}\left( {{x^3}} \right) + {{\log }_2}x + x + 1} \right] = 3.$ Mệnh đề nào sau đây là đúng?
-
A.
Nghiệm của phương trình là số nguyên âm.
-
B.
Nghiệm của phương trình là số chính phương.
-
C.
Nghiệm của phương trình là số nguyên tố.
-
D.
Nghiệm của phương trình là số vô tỉ.
Tâp nghiệm của bất phương trình \({2^{x + 2}} < {\left( {\dfrac{1}{4}} \right)^x}\) là:
-
A.
\(\left( { - \dfrac{2}{3}; + \infty } \right)\)
-
B.
\(\left( { - \infty ;0} \right)\)
-
C.
\(\left( { - \infty ; - \dfrac{2}{3}} \right)\)
-
D.
\(\left( {0; + \infty } \right)\backslash \left\{ 1 \right\}\)
Điều kiện xác định của hệ phương trình \(\left\{ \begin{array}{l}{\log _2}\left( {{x^2} - 1} \right) + {\log _2}\left( {y - 1} \right) = 1\\{3^x} = {3^y}\end{array} \right.\) là:
-
A.
\(\left\{ \begin{array}{l}x > 1\\y > 1\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x > 1 \vee x < - 1\\y > 1\end{array} \right.\)
-
C.
\(x > y > 1\)
-
D.
\(\left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\)
Tìm $m$ để phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm $x \in \left( {1;3} \right)$ .
-
A.
$- 13 < m < - 9$
-
B.
$3 < m < 9$
-
C.
$- 9 < m < 3$
-
D.
$- 13 < m < 3$
Cho phương trình \(m\ln \left( {x + 1} \right) - x - 2 = 0\). Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình đã cho có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(0 < {x_1} < 2 < 4 < {x_2}\) là khoảng \(\left( {a; + \infty } \right).\) Khi đó \(a\) thuộc khoảng nào dưới đây ?
-
A.
\(\left( {3,7;3,8} \right).\)
-
B.
\(\left( {3,6;3,7} \right).\)
-
C.
\(\left( {3,8;3,9} \right).\)
-
D.
\(\left( {3,5;3,6} \right).\)
Tập nghiệm của bất phương trình \({\left( {{x^2} + x + 1} \right)^x} < 1\) là:
-
A.
\(\left( {0; + \infty } \right)\)
-
B.
\(\left( { - \infty ;0} \right)\)
-
C.
\(\left( { - \infty ; - 1} \right)\)
-
D.
\(\left( {0;1} \right)\)
Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \(4.{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0\) nghiệm đúng với mọi giá trị \(x \in \left[ {1;64} \right]\).
-
A.
\(m < 0\).
-
B.
\(m \le 0\).
-
C.
\(m \ge 0\).
-
D.
\(m > 0\).
Lời giải và đáp án
Tổng các nghiệm của phương trình \({3^{{x^4} - 3{x^2}}} = 81\)
-
A.
$0$
-
B.
$1$
-
C.
$3$
-
D.
$4$
Đáp án : A
Đưa hai vế về dạng hai lũy thừa cùng cơ số.
\({3^{{x^4} - 3{x^2}}} = 81 = {3^4} \Leftrightarrow {x^4} - 3{x^2} - 4 = 0 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2\)
Tổng các nghiệm sẽ bằng $0$.
Tập xác định của hàm số \(f\left( x \right) = \sqrt {{{\log }_{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}}} \) là:
-
A.
\(D = \left( { - \infty ;\dfrac{{ - 3 - \sqrt {17} }}{2}} \right] \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2}; + \infty } \right)\)
-
B.
\(D = \left( { - \infty ; - 3} \right) \cup \left( {1; + \infty } \right)\)
-
C.
\(D = \left( {\dfrac{{ - 3 - \sqrt {17} }}{2}; - 3} \right) \cup \left( {\dfrac{{ - 3 + \sqrt {17} }}{2};1} \right)\)
-
D.
\(D = \left[ {\dfrac{{ - 3 - \sqrt {17} }}{2}; - 3} \right) \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2};1} \right)\)
Đáp án : D
Hàm số \(y = {\log _a}x\) xác định \( \Leftrightarrow \left\{ \begin{array}{l}x > 0\\0 < a \ne 1\end{array} \right.\)
Hàm số \(y = \sqrt A \) xác định \( \Leftrightarrow A \ge 0\)
Hàm số có dạng \(\dfrac{A}{B}\) xác định khi và chỉ khi \(B \ne 0\).
Hàm số \(f\left( x \right) = \sqrt {{{\log }_{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}}} \) xác định
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\log _{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}} \ge 0\\\dfrac{{3 - 2x - {x^2}}}{{x + 1}} > 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\log _{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}} \ge {\log _{\dfrac{1}{2}}}1\\\dfrac{{ - \left( {x - 1} \right)\left( {x + 3} \right)}}{{x + 1}} > 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{3 - 2x - {x^2}}}{{x + 1}} \le 1\\\left[ \begin{array}{l}x < - 3\\ - 1 < x < 1\end{array} \right.\\x \ne - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{3 - 2x - {x^2} - x - 1}}{{x + 1}} \le 0\\\left[ \begin{array}{l}x < - 3\\ - 1 < x < 1\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{ - {x^2} - 3x + 2}}{{x + 1}} \le 0\\\left[ \begin{array}{l}x < - 3\\ - 1 < x < 1\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}\dfrac{{ - 3 - \sqrt {17} }}{2} \le x \le - 1\\x \ge \dfrac{{ - 3 + \sqrt {17} }}{2}\end{array} \right.\\\left[ \begin{array}{l}x < - 3\\ - 1 < x < 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\dfrac{{ - 3 - \sqrt {17} }}{2} \le x < - 3\\\dfrac{{ - 3 + \sqrt {17} }}{2} \le x < 1\end{array} \right.\end{array}\)
Vậy tập xác định của phương trình là \(D = \left[ {\dfrac{{ - 3 - \sqrt {17} }}{2}; - 3} \right) \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2};1} \right)\)
Cho x>0; \(x \ne 1\) thỏa mãn biểu thức $\dfrac{1}{{{{\log }_2}x}} + \dfrac{1}{{{{\log }_3}x}} + ... + \dfrac{1}{{{{\log }_{2017}}x}} = M$ . Khi đó $x$ bằng:
-
A.
\(x = \sqrt[M]{{2017!}} - 1\)
-
B.
\(x = \sqrt[M]{{2018!}}\)
-
C.
\(x = \sqrt[M]{{2016!}}\)
-
D.
\(x = \sqrt[M]{{2017!}}\)
Đáp án : D
Biến đổi phương trình về phương trình logarit cơ bản.
Sử dụng công thức ${\log _a}b = \dfrac{1}{{{{\log }_b}a}}$
\( \begin{array}{l} VT= {\log _x}2 + {\log _x}3 + {\log _x}4 + ... + {\log _x}2017 = {\log _x}(2.3.4...2017)\\ \Rightarrow {x^M} = 2017! \Rightarrow x = \sqrt[M]{{2017!}}\end{array}\)
Tập nghiệm của bất phương trình \({\left( {2 + \sqrt 3 } \right)^{\dfrac{{x - 3}}{{x - 1}}}} < {\left( {2 - \sqrt 3 } \right)^{\dfrac{{x - 1}}{{x - 3}}}}\) là :
-
A.
\(1 - \sqrt 3 \le x \le 0\)
-
B.
\(2 \le x \le 1 + \sqrt 3 \)
-
C.
\(1 - \sqrt 3 \le x \le 0 \cup 2 \le x \le 1 + \sqrt 3 \)
-
D.
\(1 - \sqrt 3 \le x \le 0 \cap 2 \le x \le 1 + \sqrt 3 \)
Đáp án : B
Nhận thấy \(\left( {2 + \sqrt 3 } \right)\left( {2 - \sqrt 3 } \right) = 1\), đưa bất phương trinh về cùng cơ số \(2 + \sqrt 3 \).
\({a^x} < {a^y} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}0 < a < 1\\x > y\end{array} \right.\\\left\{ \begin{array}{l}a > 1\\x < y\end{array} \right.\end{array} \right.\)
TXĐ : \(x \ne 3,x \ne 1.\)
Ta có \(\left( {2 + \sqrt 3 } \right)\left( {2 - \sqrt 3 } \right) = 1 \Rightarrow 2 - \sqrt 3 = \dfrac{1}{{2 + \sqrt 3 }} = {\left( {2 + \sqrt 3 } \right)^{ - 1}}\)
\( \Rightarrow {\left( {2 + \sqrt 3 } \right)^{\dfrac{{x - 3}}{{x - 1}}}} < {\left( {2 + \sqrt 3 } \right)^{ - \dfrac{{x - 1}}{{x - 3}}}}\)
Ta có : \(2 + \sqrt 3 > 1 \Rightarrow \dfrac{{x - 3}}{{x - 1}} < - \dfrac{{x - 1}}{{x - 3}} \Leftrightarrow \dfrac{{x - 3}}{{x - 1}} + \dfrac{{x - 1}}{{x - 3}} < 0 \Leftrightarrow \dfrac{{{{\left( {x - 3} \right)}^2} + {{\left( {x - 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {x - 3} \right)}} < 0\)
Ta có \({\left( {x - 3} \right)^2} + {\left( {x - 1} \right)^2} \ge 0\,\,\forall x \in R\backslash \left\{ {1;3} \right\} \Rightarrow \left( {x - 1} \right)\left( {x - 3} \right) < 0 \Leftrightarrow x \in \left( {1;3} \right)\)
Dựa vào các đáp án ta thấy chỉ có đáp án B là tập con của tập \(\left( {1;3} \right)\)
Phương trình \({4^{2x + 5}} = {2^{2 - x}}\) có nghiệm là:
-
A.
\(\dfrac{{ - 8}}{5}\)
-
B.
\(3\)
-
C.
\(\dfrac{8}{5}\)
-
D.
\(\dfrac{{12}}{5}\)
Đáp án : A
Giải phương trình mũ bằng cách đưa về cùng cơ số là biến đổi về dạng ${a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Leftrightarrow f\left( x \right) = g\left( x \right)$
${4^{2{\rm{x}} + 5}} = {2^{2 - x}} \Leftrightarrow {2^{4{\rm{x}} + 10}} = {2^{2 - x}} \Leftrightarrow 4{\rm{x}} + 10 = 2 - x \Leftrightarrow 5{\rm{x}} = - 8 \Leftrightarrow x = \dfrac{{ - 8}}{5}$
Cho phương trình ${\log _2}\left[ {{{\log }_{\dfrac{1}{8}}}\left( {{x^3}} \right) + {{\log }_2}x + x + 1} \right] = 3.$ Mệnh đề nào sau đây là đúng?
-
A.
Nghiệm của phương trình là số nguyên âm.
-
B.
Nghiệm của phương trình là số chính phương.
-
C.
Nghiệm của phương trình là số nguyên tố.
-
D.
Nghiệm của phương trình là số vô tỉ.
Đáp án : C
Dùng phương pháp đưa về cùng cơ số \(2\), giải phương trình thu được và kết luận.
Điều kiện: $x > 0.$
Phương trình $ \Leftrightarrow {\log _2}\left[ { - {{\log }_2}x + {{\log }_2}x + x + 1} \right] = 3$
$ \Leftrightarrow {\log _2}\left( {x + 1} \right) = 3$ $ \Leftrightarrow x + 1 = 8 \Leftrightarrow x = 7\left( {TM} \right)$
Tâp nghiệm của bất phương trình \({2^{x + 2}} < {\left( {\dfrac{1}{4}} \right)^x}\) là:
-
A.
\(\left( { - \dfrac{2}{3}; + \infty } \right)\)
-
B.
\(\left( { - \infty ;0} \right)\)
-
C.
\(\left( { - \infty ; - \dfrac{2}{3}} \right)\)
-
D.
\(\left( {0; + \infty } \right)\backslash \left\{ 1 \right\}\)
Đáp án : C
Đưa bất phương trình về cùng cơ số 2.
\({a^x} \le {a^y} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}0 < a < 1\\x \ge y\end{array} \right.\\\left\{ \begin{array}{l}a > 1\\x \le y\end{array} \right.\end{array} \right.\)
\({2^{x + 2}} < {\left( {\dfrac{1}{4}} \right)^x} \Leftrightarrow {2^{x + 2}} < {\left( {{2^{ - 2}}} \right)^x} \Leftrightarrow {2^{x + 2}} < {2^{ - 2x}}\)
Vì \(2 > 1 \Rightarrow x + 2 < - 2x \Leftrightarrow 3x < - 2 \Leftrightarrow x < - \dfrac{2}{3}\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - \dfrac{2}{3}} \right)\)
Điều kiện xác định của hệ phương trình \(\left\{ \begin{array}{l}{\log _2}\left( {{x^2} - 1} \right) + {\log _2}\left( {y - 1} \right) = 1\\{3^x} = {3^y}\end{array} \right.\) là:
-
A.
\(\left\{ \begin{array}{l}x > 1\\y > 1\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x > 1 \vee x < - 1\\y > 1\end{array} \right.\)
-
C.
\(x > y > 1\)
-
D.
\(\left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\)
Đáp án : B
Sử dụng điều kiện để hàm số \(y = {\log _a}x\) xác định.
Điều kiện xác định: \(\left\{ \begin{array}{l}{x^2} - 1 > 0\\y - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 1 \vee x < - 1\\y > 1\end{array} \right.\)
Tìm $m$ để phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm $x \in \left( {1;3} \right)$ .
-
A.
$- 13 < m < - 9$
-
B.
$3 < m < 9$
-
C.
$- 9 < m < 3$
-
D.
$- 13 < m < 3$
Đáp án : A
- Đặt ẩn phụ đưa phương trình về bậc hai.
- Tìm điều kiện để bài toán phụ có nghiệm thỏa mãn điều kiện của ẩn phụ,
Đặt $t = {2^x};x \in \left( {1;3} \right) \Rightarrow t = {2^x} \in \left( {2;8} \right)$
Xét hàm số \(y = {t^2} - 8t + 3\) trên \((2;8)\) có:
$y' = 2t - 8;$ $y' = 0 \Leftrightarrow 2t - 8 = 0 \Leftrightarrow t = 4\in (2;8)$
Bảng biến thiên:
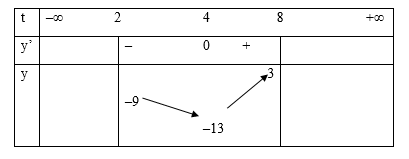
Căn cứ bảng biến thiên:
Phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm \(x \in \left( {1;3} \right) \Leftrightarrow - 13 < m < - 9\)
Cho phương trình \(m\ln \left( {x + 1} \right) - x - 2 = 0\). Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình đã cho có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(0 < {x_1} < 2 < 4 < {x_2}\) là khoảng \(\left( {a; + \infty } \right).\) Khi đó \(a\) thuộc khoảng nào dưới đây ?
-
A.
\(\left( {3,7;3,8} \right).\)
-
B.
\(\left( {3,6;3,7} \right).\)
-
C.
\(\left( {3,8;3,9} \right).\)
-
D.
\(\left( {3,5;3,6} \right).\)
Đáp án : A
- Cô lập \(m\), đưa phương trình về dạng \(m = f\left( x \right)\).
- Khảo sát và lập BBT của hàm số \(f\left( x \right)\), từ đó suy ra điều kiện của \(m\) để thỏa mãn yêu cầu bài toán.
ĐKXĐ: \(x > - 1\).
Ta có: \(m\ln \left( {x + 1} \right) - x - 2 = 0 \Leftrightarrow m\ln \left( {x + 1} \right) = x + 2\) (1)
Dễ dàng kiểm tra \(x = 0\) không phải nghiệm của phương trình trên.
Với \(x \ne 0\), phương trình \(\left( 1 \right) \Leftrightarrow m = \dfrac{{x + 2}}{{\ln \left( {x + 1} \right)}}\)
Xét hàm số \(f\left( x \right) = \dfrac{{x + 2}}{{\ln \left( {x + 1} \right)}}\,\,\left( {x > - 1,\,\,x \ne 0} \right)\) ta có: \(f'\left( x \right) = \dfrac{{\ln \left( {x + 1} \right) - \dfrac{{x + 2}}{{x + 1}}}}{{{{\ln }^2}\left( {x + 1} \right)}}\)
Nhận xét: Trên \(\left( { - 1; + \infty } \right)\backslash \left\{ 0 \right\}\), hàm số \(y = \ln (x + 1)\) đồng biến, hàm số \(y = \dfrac{{x + 2}}{{x + 1}}\) nghịch biến
\( \Rightarrow g\left( x \right) = \ln \left( {x + 1} \right) - \dfrac{{x + 2}}{{x + 1}} = 0\) (2) có tối đa 1 nghiệm trên \(\left( {1; + \infty } \right)\).
Mà \(g\left( 2 \right) = \ln 3 - \dfrac{4}{3} < 0,\,\,g\left( 4 \right) = \ln 5 - \dfrac{6}{5} > 0 \Rightarrow \) PT (2) có nghiệm duy nhất \({x_0} \in \left( {2;4} \right)\).
Ta có BBT của \(f\left( x \right)\) trên 2 khoảng \(\left( {0;2} \right)\) và \(\left( {4; + \infty } \right)\) như sau:
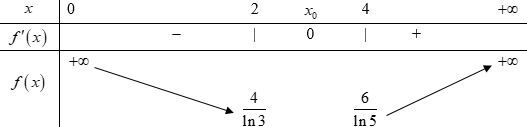
\(\left( {\dfrac{4}{{\ln 3}} \approx 3,64,\,\,\dfrac{6}{{\ln 5}} \approx 3,73} \right)\)
Như vậy, để phương trình đã cho có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(0 < {x_1} < 2 < 4 < {x_2}\) thì \(m > \dfrac{6}{{\ln 5}} \approx 3,73\,\).
Tập nghiệm của bất phương trình \({\left( {{x^2} + x + 1} \right)^x} < 1\) là:
-
A.
\(\left( {0; + \infty } \right)\)
-
B.
\(\left( { - \infty ;0} \right)\)
-
C.
\(\left( { - \infty ; - 1} \right)\)
-
D.
\(\left( {0;1} \right)\)
Đáp án : C
Sử dụng phương pháp loganepe hai vế để giải bất phương trình.
Phương pháp giải bất phương trình tích: \(f\left( x \right)g\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) < 0\\g\left( x \right) > 0\end{array} \right.\\\left\{ \begin{array}{l}f\left( x \right) > 0\\g\left( x \right) < 0\end{array} \right.\end{array} \right.\)
\({\left( {{x^2} + x + 1} \right)^x} < 1\)
Lấy loganepe hai vế ta có \(\ln {\left( {{x^2} + x + 1} \right)^x} < \ln 1\,\,\left( * \right)\)
Vì \({x^2} + x + 1 = {\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} > 0 \Rightarrow \left( * \right) \Leftrightarrow x\ln \left( {{x^2} + x + 1} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 0\\\ln \left( {{x^2} + x + 1} \right) > 0\end{array} \right.\\\left\{ \begin{array}{l}x > 0\\\ln \left( {{x^2} + x + 1} \right) < 0\end{array} \right.\end{array} \right.\)
$ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 0\\{x^2} + x + 1 > 1\end{array} \right.\\\left\{ \begin{array}{l}x > 0\\{x^2} + x + 1 < 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 0\\{x^2} + x > 0\end{array} \right.\\\left\{ \begin{array}{l}x > 0\\{x^2} + x < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 0\\\left[ \begin{array}{l}x > 0\\x < - 1\end{array} \right.\end{array} \right.\\\left\{ \begin{array}{l}x > 0\\ - 1 < x < 0\end{array} \right.\end{array} \right. \Leftrightarrow x < - 1$
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right)\).
Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \(4.{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0\) nghiệm đúng với mọi giá trị \(x \in \left[ {1;64} \right]\).
-
A.
\(m < 0\).
-
B.
\(m \le 0\).
-
C.
\(m \ge 0\).
-
D.
\(m > 0\).
Đáp án : C
Đặt ẩn phụ đưa về bất phương trình đại số.
Điều kiện : $x > 0$
\(4.{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0 \Leftrightarrow 4.{\left( {{{\log }_2}\sqrt x } \right)^2} + 2.{\log _2}\sqrt x \ge - m\)(1)
Đặt \(t = {\log _2}\sqrt x \). Khi \(x \in \left[ {1;64} \right] \Rightarrow t \in \left[ {0;3} \right]\).
Ta có bất phương trình \(4{t^2} + 2t \ge - m\).
Xét \(f(t) = 4{t^2} + 2t;f'(t) = 8t + 2 > 0,\forall t \in \left[ {0;3} \right]\)
Để (1) nghiệm đúng với \(\forall t \in \left[ {0;3} \right]\) thì $\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( t \right) \ge - m$
\( \Leftrightarrow f(0) \ge - m \Leftrightarrow 0 \ge - m \Leftrightarrow m \ge 0\).
>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.
 |
 |
 |
 |
 |
 |
 |
 |
