Đề kiểm tra 1 tiết Toán 12 chương 5: Khối đa diện và thể tích - Đề số 2
Đề bài
Cho khối chóp \(S.ABC\). Trên các cạnh \(SA,SB,SC\) lấy các điểm \(A',B',C'\) sao cho \(A'A = 2SA',B'B = 2SB',C'C = 2SC'\), khi đó tồn tại một phép vị tự biến khối chóp \(S.ABC\) thành khối chóp \(S.A'B'C'\) với tỉ số đồng dạng là:
-
A.
\(k = \dfrac{1}{2}\)
-
B.
\(k = 2\)
-
C.
\(k = \dfrac{1}{3}\)
-
D.
\(k = 3\)
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là tứ giác đều cạnh $a$, biết rằng \(BD' = a\sqrt 6 \) . Tính thể tích của khối lăng trụ?
-
A.
\({a^3}\sqrt 2 \)
-
B.
\({a^3}\sqrt 3 \)
-
C.
\(3{a^3}\)
-
D.
\(2{a^3}\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông, \(SA\) vuông góc với đáy. Hình chóp có bao nhiêu mặt bên là tam giác vuông?
-
A.
\(1\) mặt
-
B.
\(2\) mặt
-
C.
\(3\) mặt
-
D.
\(4\) mặt
Cho khối lập phương có thể tích bằng 27, diện tích toàn phần của khối lập phương đã cho bằng:
-
A.
\(75\)
-
B.
\(36\)
-
C.
\(18\)
-
D.
\(54\)
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
-
A.
1
-
B.
4
-
C.
2
-
D.
3
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:
-
A.
\(\dfrac{{2{a^3}\sqrt 2 }}{3}\)
-
B.
\(\dfrac{{{a^3}\sqrt 2 }}{6}\)
-
C.
\(\dfrac{{2{a^3}}}{3}\)
-
D.
\(\dfrac{{{a^3}\sqrt 2 }}{{12}}\)
Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng:
-
A.
\(V = Sh\)
-
B.
\(V = \dfrac{1}{2}Sh\)
-
C.
\(V = \dfrac{1}{3}Sh\)
-
D.
\(V = \dfrac{1}{6}Sh\)
Đa diện đều loại \(\left\{ {5;3} \right\}\) có tên gọi nào dưới đây?
-
A.
Tứ diện đều
-
B.
Bát diện đều
-
C.
Hai mươi mặt đều
-
D.
Mười hai mặt đều
Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là \(6cm\) và \(8cm\), biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ
-
A.
\(480c{m^3}\)
-
B.
\(360c{m^3}\)
-
C.
\(240c{m^3}\)
-
D.
\(120c{m^3}\)
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất:
-
A.
Năm mặt
-
B.
Hai mặt
-
C.
Ba mặt
-
D.
Bốn mặt
Cho đoạn thẳng \(AB\). Mặt phẳng \(\left( P \right)\) là mặt phẳng trung trực của \(AB\) thì:
-
A.
\(A,B\) đối xứng nhau qua \(\left( P \right)\).
-
B.
\(AB \subset \left( P \right)\).
-
C.
\(AB//\left( P \right)\).
-
D.
\(A \in \left( P \right),B \notin \left( P \right)\).
Cho hình chóp đều $S.ABCD$ có diện tích đáy là \(16c{m^2}\), diện tích một mặt bên là \(8\sqrt 3 c{m^2}\). Thể tích khối chóp $S.ABCD$ là:
-
A.
\(\dfrac{{32\sqrt 2 }}{3}c{m^3}\)
-
B.
\(\dfrac{{32\sqrt {13} }}{3}c{m^3}\)
-
C.
\(\dfrac{{32\sqrt {11} }}{3}c{m^3}\)
-
D.
\(4c{m^3}\)
Trong các khẳng định sau, khẳng định nào sai?
-
A.
Lắp ghép 2 khối hộp sẽ được một khối đa diện lồi.
-
B.
Khối tứ diện là khối đa diện lồi.
-
C.
Khối hộp là khối đa diện lồi.
-
D.
Khối lăng trụ tam giác là khối đa diện lồi.
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác cân tại \(C,\,\,A'C = a\sqrt 5 ,\)\(BC = a,\,\,\angle ACB = {45^0}.\) Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
-
A.
\({a^3}\sqrt 3 \)
-
B.
\(\dfrac{{{a^3}\sqrt 2 }}{2}\)
-
C.
\(\dfrac{{{a^3}\sqrt 2 }}{6}\)
-
D.
\(\dfrac{{{a^3}\sqrt 2 }}{{12}}\)
Có bao nhiêu cách chọn ra ba đỉnh từ các đỉnh của một hình lập phương để thu được một tam giác đều ?
-
A.
\(12.\)
-
B.
\(10.\)
-
C.
\(4.\)
-
D.
\(8.\)
Mệnh đề nào sau đây là mệnh đề đúng?
-
A.
Tồn tại một đa diện đều có $2$ mặt là $2$ đa giác không bằng nhau.
-
B.
Nếu hình chóp tứ giác $S.ABCD$ là hình chóp đều thì nó cũng là đa diện đều
-
C.
Nếu một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của đúng $3$ mặt thì tổng số đỉnh của nó phải là số chẵn.
-
D.
Nếu lăng trụ tam giác $ABC.A'B'C'$ là lăng trụ đều thì nó cũng là đa diện đều.
Cho hình chóp tứ giác đều $S.ABCD$ có chiều cao $h$, góc ở đỉnh của mặt bên bằng \({60^0}\). Thể tích hình chóp là:
-
A.
\(\dfrac{{3{h^3}}}{2}\)
-
B.
\(\dfrac{{{h^3}}}{3}\)
-
C.
\(\dfrac{{2{h^3}}}{3}\)
-
D.
\(\dfrac{{{h^3}\sqrt 3 }}{3}\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Đường thẳng \(SC\) tạo với đáy góc \({45^0}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\). Thể tích của khối chóp \(S.MCDN\) là:
-
A.
\(\dfrac{{5{a^3}\sqrt 2 }}{{12}}\)
-
B.
\(\dfrac{{5{a^3}\sqrt 2 }}{6}\)
-
C.
\(\dfrac{{5{a^3}\sqrt 2 }}{8}\)
-
D.
\(\dfrac{{5{a^3}\sqrt 2 }}{{24}}\)
Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng \(4\) và tạo với đáy góc \({60^0}\). Thể tích của khối chóp đó là:
-
A.
\(16\)
-
B.
\(8\sqrt 3 \)
-
C.
\(48\sqrt 3 \)
-
D.
\(16\sqrt 3 \)
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. Cho \(\widehat {BAA'} = {45^0}\). Thể tích của khối lăng trụ đã cho là:
-
A.
\(\dfrac{{{a^3}\sqrt 2 }}{4}\)
-
B.
\(\dfrac{{{a^3}\sqrt 2 }}{8}\)
-
C.
\(\dfrac{{{a^3}}}{8}\)
-
D.
\(\dfrac{{{a^3}}}{4}\)
Cho hình hộp \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thoi cạnh $a\sqrt 3 ,{\mkern 1mu} BD = 3a,$ hình chiếu vuông góc của \(B\) trên mặt phẳng $\left( {A'B'C'D'} \right)$ trùng với trung điểm của \(A’C’\). Gọi $\alpha $ là góc tạo bởi hai mặt phẳng $\left( {ABCD} \right)$ và $\left( {CDD'C'} \right), \cos \alpha = \dfrac{{\sqrt {21} }}{7}$ . Thể tích của khối hộp \(ABCD.A’B’C’D\) bằng
-
A.
$\dfrac{{3{a^3}}}{4}$
-
B.
$\dfrac{{9\sqrt 3 {a^3}}}{4}$
-
C.
$\dfrac{{9{a^3}}}{4}$
-
D.
$\dfrac{{3\sqrt 3 {a^3}}}{4}$
Cho lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $a$, và \(A'A = A'B = A'C = a\sqrt {\dfrac{7}{{12}}} \) . Thể tích khối lăng trụ \(ABC.A'B'C'\) theo $a$ là:
-
A.
\(\dfrac{{{a^3}}}{8}\)
-
B.
\(\dfrac{{{a^3}\sqrt 3 }}{8}\)
-
C.
\(\dfrac{{3{a^3}\sqrt 3 }}{8}\)
-
D.
\(\dfrac{{{a^3}\sqrt 3 }}{4}\)
Cho tứ diện \(ABCD\) có \(G\) là điểm thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Mặt phẳng thay đổi chứa \(BG\) và cắt \(AC,\,\,AD\) lần lượt tại \(M\) và \(N\). Giá trị nhỏ nhất của tỉ số \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}}\) là
-
A.
\(\dfrac{3}{8}\)
-
B.
\(\dfrac{4}{9}\)
-
C.
\(\dfrac{1}{2}\)
-
D.
\(\dfrac{5}{9}\)
Đề thi THPT QG - 2021 - mã 101
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 2a,\) góc giữa hai mặt phẳng \(\left( {A'B{\rm{D}}} \right)\) và \(\left( {ABCD} \right)\) bằng \({30^0}\). Thể tích của khối hộp chữ nhật đã cho bằng
-
A.
\(6\sqrt 3 \,{a^3}.\)
-
B.
\(\dfrac{{2\sqrt 3 }}{9}{a^3}.\)
-
C.
\(2\sqrt 3 {a^3}.\)
-
D.
\(\dfrac{{2\sqrt 3 }}{3}{a^3}.\)
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\)
-
A.
\(3\)
-
B.
\(2\sqrt 2 \)
-
C.
\(2\sqrt 3 \)
-
D.
\(4\)
Lời giải và đáp án
Cho khối chóp \(S.ABC\). Trên các cạnh \(SA,SB,SC\) lấy các điểm \(A',B',C'\) sao cho \(A'A = 2SA',B'B = 2SB',C'C = 2SC'\), khi đó tồn tại một phép vị tự biến khối chóp \(S.ABC\) thành khối chóp \(S.A'B'C'\) với tỉ số đồng dạng là:
-
A.
\(k = \dfrac{1}{2}\)
-
B.
\(k = 2\)
-
C.
\(k = \dfrac{1}{3}\)
-
D.
\(k = 3\)
Đáp án : C
Ta có: \(A'A = 2SA',B'B = 2SB',C'C = 2SC' \)
$\Rightarrow \overrightarrow {SA'} = \dfrac{1}{3}\overrightarrow {SA} ,\overrightarrow {SB'} = \dfrac{1}{3}\overrightarrow {SB} ,\overrightarrow {SC'} = \dfrac{1}{3}\overrightarrow {SC} $
Do đó phép vị tự tâm \(S\) tỉ số \(k = \dfrac{1}{3}\) biến các điểm \(A,B,C\) thành \(A',B',C'\).
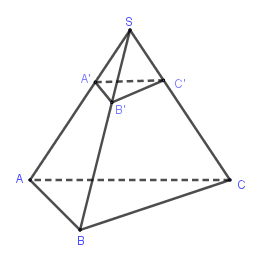
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là tứ giác đều cạnh $a$, biết rằng \(BD' = a\sqrt 6 \) . Tính thể tích của khối lăng trụ?
-
A.
\({a^3}\sqrt 2 \)
-
B.
\({a^3}\sqrt 3 \)
-
C.
\(3{a^3}\)
-
D.
\(2{a^3}\)
Đáp án : D
- Tính diện tích đáy \({S_{A'B'C'D'}}\) và độ dài đường cao \(BB'\).
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\).
Vì $A'B'C'D'$ là hình vuông cạnh $a$ nên \(B'D' = a\sqrt 2 \)
\(BB' \bot \left( {A'B'C'D'} \right) \Rightarrow BB' \bot B'D' \Rightarrow \Delta BB'D'\) vuông tại \(B' \Rightarrow BB' = \sqrt {BD{'^2} - B'D{'^2}} = \sqrt {6{a^2} - 2{a^2}} = 2a\)
Vậy \({V_{ABCD.A'B'C'D'}} = BB'.{S_{ABCD}} = 2a.{a^2} = 2{a^3}\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông, \(SA\) vuông góc với đáy. Hình chóp có bao nhiêu mặt bên là tam giác vuông?
-
A.
\(1\) mặt
-
B.
\(2\) mặt
-
C.
\(3\) mặt
-
D.
\(4\) mặt
Đáp án : D
Dựng hình và tìm các tam giác vuông trong số bốn mặt bên của hình chóp.
Sử dụng định lý: “Đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó”
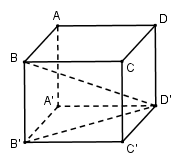
Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AD,SA \bot AB \Rightarrow \Delta SAB,\Delta SAD\) vuông tại \(A\).
Lại có \(CD \bot SA,CD \bot AD \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD \Rightarrow \Delta SCD\) vuông tại $D.$
\(CB \bot SA,CB \bot AB \Rightarrow CB \bot \left( {SAB} \right) \Rightarrow CB \bot SB \Rightarrow \Delta SCB\) vuông tại \(B\).
Vậy có tất cả $4$ mặt là các tam giác vuông.
Cho khối lập phương có thể tích bằng 27, diện tích toàn phần của khối lập phương đã cho bằng:
-
A.
\(75\)
-
B.
\(36\)
-
C.
\(18\)
-
D.
\(54\)
Đáp án : D
Thể tích khối lập phương cạnh \(a\) là: \(V = {a^3}.\)
Diện tích toàn phần của khối lập phương cạnh \(a\) là: \({S_{tp}} = 6{a^2}.\)
Cạnh của khối lập phương đã cho là:\(a = \sqrt[3]{{27}} = 3.\)
\( \Rightarrow \) Diện tích toàn phần của khối lập phương đã cho là: \({6.3^2} = 54.\)
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
-
A.
1
-
B.
4
-
C.
2
-
D.
3
Đáp án : B
Dựa vào khái niệm mặt đối xứng của khối đa diện.
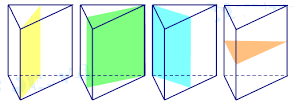
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng như hình vẽ dưới:
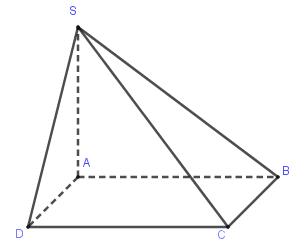
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:
-
A.
\(\dfrac{{2{a^3}\sqrt 2 }}{3}\)
-
B.
\(\dfrac{{{a^3}\sqrt 2 }}{6}\)
-
C.
\(\dfrac{{2{a^3}}}{3}\)
-
D.
\(\dfrac{{{a^3}\sqrt 2 }}{{12}}\)
Đáp án : B
- Bước 1: Tính diện tích đáy \({S_{\Delta BCD}}\), dựa vào các tính chất của đáy.
- Bước 2: Tính chiều cao \(h = SA\).
- Bước 3: Tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
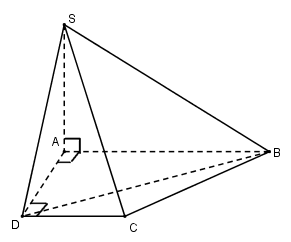
Ta có: \({S_{ABCD}} = \dfrac{1}{2}\left( {AB + CD} \right).AD = \dfrac{1}{2}\left( {2a + a} \right)a = \dfrac{{3{a^2}}}{2}\)
\({S_{\Delta ABD}} = \dfrac{1}{2}AD.AB = \dfrac{1}{2}a.2a = {a^2}\)
\( \Rightarrow {S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = \dfrac{{3{a^2}}}{2} - {a^2} = \dfrac{{{a^2}}}{2}\)
\(SA = \dfrac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \)
\( \Rightarrow {V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng:
-
A.
\(V = Sh\)
-
B.
\(V = \dfrac{1}{2}Sh\)
-
C.
\(V = \dfrac{1}{3}Sh\)
-
D.
\(V = \dfrac{1}{6}Sh\)
Đáp án : C
Công thức tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Đa diện đều loại \(\left\{ {5;3} \right\}\) có tên gọi nào dưới đây?
-
A.
Tứ diện đều
-
B.
Bát diện đều
-
C.
Hai mươi mặt đều
-
D.
Mười hai mặt đều
Đáp án : D
Khối đa diện đều loại \(\left\{ {p;q} \right\}\) là khối đa diện lồi thỏa mãn mỗi mặt của nó là đa giác đều \(p\) cạnh và mỗi đỉnh của nó là đỉnh chung của đúng \(q\) mặt.
Đa diện đều loại \(\left\{ {5;3} \right\}\) có tên gọi là Mười hai mặt đều.
Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là \(6cm\) và \(8cm\), biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ
-
A.
\(480c{m^3}\)
-
B.
\(360c{m^3}\)
-
C.
\(240c{m^3}\)
-
D.
\(120c{m^3}\)
Đáp án : C
- Tính độ dài cạnh hình thoi, từ đó suy ra chu vi đáy và chiều cao lăng trụ.
- Tính diện tích đáy hình thoi \({S_{ABCD}} = \dfrac{1}{2}AC.BD\).
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\).
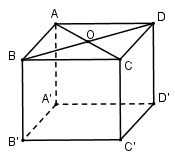
Gọi \(O = AC \cap BD\) ta có: \(OA = 3cm\,;\,OB = 4cm\)
Xét tam giác vuông $OAB$ có: \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{3^2} + {4^2}} = 5cm\).
Khi đó chu vi đáy bằng \(P = 4.5 = 20 = 2AA' \Rightarrow AA' = 10\left( {cm} \right)\)
\({S_{ABCD}} = \dfrac{1}{2}AC.BD = \dfrac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Vậy \({V_{ABCD.A'B'C'D'}} = AA'.{S_{ABCD}} = 10.24 = 240\left( {c{m^3}} \right)\)
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất:
-
A.
Năm mặt
-
B.
Hai mặt
-
C.
Ba mặt
-
D.
Bốn mặt
Đáp án : C
Sử dụng phương pháp chọn điểm rơi, lấy ví dụ cho hình tứ diện và suy ra đáp án.
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất 3 mặt (ví dụ các đỉnh của hình tứ diện)
Không tồn tại 1 đỉnh nào đó của đa diện nào đó là đỉnh chung của ít hơn 3 mặt
Cho đoạn thẳng \(AB\). Mặt phẳng \(\left( P \right)\) là mặt phẳng trung trực của \(AB\) thì:
-
A.
\(A,B\) đối xứng nhau qua \(\left( P \right)\).
-
B.
\(AB \subset \left( P \right)\).
-
C.
\(AB//\left( P \right)\).
-
D.
\(A \in \left( P \right),B \notin \left( P \right)\).
Đáp án : A
Hai điểm \(A,A'\) đối xứng nhau qua mặt phẳng \(\left( P \right)\) nếu \(\left( P \right)\) là mặt phẳng trung trực của \(AB\)
Mặt phẳng \(\left( P \right)\) là mặt phẳng trung trực của \(AB\) thì \(A,B\) đối xứng nhau qua \(\left( P \right)\).
Cho hình chóp đều $S.ABCD$ có diện tích đáy là \(16c{m^2}\), diện tích một mặt bên là \(8\sqrt 3 c{m^2}\). Thể tích khối chóp $S.ABCD$ là:
-
A.
\(\dfrac{{32\sqrt 2 }}{3}c{m^3}\)
-
B.
\(\dfrac{{32\sqrt {13} }}{3}c{m^3}\)
-
C.
\(\dfrac{{32\sqrt {11} }}{3}c{m^3}\)
-
D.
\(4c{m^3}\)
Đáp án : C
- Gọi \(E\) là trung điểm của \(AB\), tính \(OE,SE \Rightarrow SO\).
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).
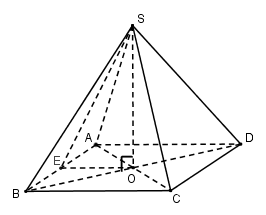
Gọi \(O = AC \cap BD\). Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Vì chóp $S.ABCD$ đều nên $ABCD$ là hình vuông \( \Rightarrow {S_{ABCD}} = A{B^2} = 16 \Rightarrow AB = 4\left( {cm} \right) = AD\)
Gọi $E$ là trung điểm của AB\( \Rightarrow OE\) là đường trung bình của tam giác ABD\( \Rightarrow OE//AD \Rightarrow OE \bot AB\) và \(OE = \dfrac{1}{2}AD = \dfrac{1}{2}.4 = 2\left( {cm} \right)\)
\(\left. \begin{array}{l}OE \bot AB\\SO \bot AB\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow AB \bot \left( {SOE} \right) \Rightarrow AB \bot SE\)
\( \Rightarrow {S_{\Delta SAB}} = \dfrac{1}{2}SE.AB = 8\sqrt 3 \Rightarrow SE = \dfrac{{16\sqrt 3 }}{{AB}} = \dfrac{{16\sqrt 3 }}{4} = 4\sqrt 3 \left( {cm} \right)\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OE \Rightarrow \Delta SOE\) vuông tại O\( \Rightarrow SO = \sqrt {S{E^2} - O{E^2}} = \sqrt {48 - 4} = \sqrt {44} = 2\sqrt {11} \left( {cm} \right)\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.2\sqrt {11} .16 = \dfrac{{32\sqrt {11} }}{3}\left( {c{m^3}} \right)\)
Trong các khẳng định sau, khẳng định nào sai?
-
A.
Lắp ghép 2 khối hộp sẽ được một khối đa diện lồi.
-
B.
Khối tứ diện là khối đa diện lồi.
-
C.
Khối hộp là khối đa diện lồi.
-
D.
Khối lăng trụ tam giác là khối đa diện lồi.
Đáp án : A
Các khối tứ diện, khối hộp, khối lăng trụ tam giác đều là khối đa diện lồi.
Lắp ghép 2 khối hộp chưa chắc được một khối đa diện lồi.
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác cân tại \(C,\,\,A'C = a\sqrt 5 ,\)\(BC = a,\,\,\angle ACB = {45^0}.\) Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
-
A.
\({a^3}\sqrt 3 \)
-
B.
\(\dfrac{{{a^3}\sqrt 2 }}{2}\)
-
C.
\(\dfrac{{{a^3}\sqrt 2 }}{6}\)
-
D.
\(\dfrac{{{a^3}\sqrt 2 }}{{12}}\)
Đáp án : B
Thể tích khối lăng trụ có chiều cao \(h\) và diện tích đáy \(S\) là \(V = Sh.\)
Diện tích tam giác \(ABC\) là: \(S = \dfrac{1}{2}AC.BC.\sin C.\)
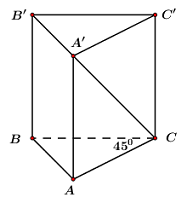
Ta có: \(\Delta ABC\) cân tại \(C\) \( \Rightarrow AC = BC = a.\)
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AC.BC.\sin C\) \( = \dfrac{1}{2}.a.a.\sin {45^0}\)\( = \dfrac{1}{2}{a^2}.\dfrac{{\sqrt 2 }}{2} = \dfrac{{{a^2}\sqrt 2 }}{4}.\)
Áp dụng định lý Pitago cho \(\Delta AA'C\) vuông tại \(A\) ta có:
\(AA' = \sqrt {A'{C^2} - A{C^2}} \) \( = \sqrt {5{a^2} - {a^2}} = 2a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{ABC}}\) \( = 2a.\dfrac{{{a^2}\sqrt 2 }}{4} = \dfrac{{{a^3}\sqrt 2 }}{2}.\)
Có bao nhiêu cách chọn ra ba đỉnh từ các đỉnh của một hình lập phương để thu được một tam giác đều ?
-
A.
\(12.\)
-
B.
\(10.\)
-
C.
\(4.\)
-
D.
\(8.\)
Đáp án : D
- Nối các đường chéo của các mặt của hình lập phương.
- Đếm số tam giác đều.
Nối các đường chéo của các mặt ta được 2 tứ diện đều không có đỉnh nào chung.
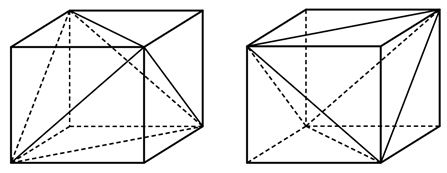
Mỗi tứ diện đều có 4 tmặt là 4 tam giác đều. Nên tổng cộng có 8 tam giác đều.
Mệnh đề nào sau đây là mệnh đề đúng?
-
A.
Tồn tại một đa diện đều có $2$ mặt là $2$ đa giác không bằng nhau.
-
B.
Nếu hình chóp tứ giác $S.ABCD$ là hình chóp đều thì nó cũng là đa diện đều
-
C.
Nếu một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của đúng $3$ mặt thì tổng số đỉnh của nó phải là số chẵn.
-
D.
Nếu lăng trụ tam giác $ABC.A'B'C'$ là lăng trụ đều thì nó cũng là đa diện đều.
Đáp án : C
Đa diện đều có tất cả các mặt là các đa giác bằng nhau.
Không tồn tại đa diện đều có $5$ và $6$ đỉnh, do đó chóp $S.ABCD$ và lăng trụ $ABC.A'B'C'$ không thể là đa diện đều.
Nếu mỗi đỉnh là đỉnh chung của đúng $3$ mặt thì nó cũng là đỉnh chung của đúng $3$ cạnh. Giả sử số đỉnh của đa diện là $n$ thì số cạnh của nó phải là $\dfrac{{3n}}{2}$ (vì mỗi cạnh được tính $2$ lần), do đó $n$ chẵn.
Cho hình chóp tứ giác đều $S.ABCD$ có chiều cao $h$, góc ở đỉnh của mặt bên bằng \({60^0}\). Thể tích hình chóp là:
-
A.
\(\dfrac{{3{h^3}}}{2}\)
-
B.
\(\dfrac{{{h^3}}}{3}\)
-
C.
\(\dfrac{{2{h^3}}}{3}\)
-
D.
\(\dfrac{{{h^3}\sqrt 3 }}{3}\)
Đáp án : C
- Bước 1: Tính diện tích đáy \(S\)
- Bước 2: Tính chiều cao \(h\).
- Bước 3: Tính thể tích \(V = \dfrac{1}{3}Sh\).
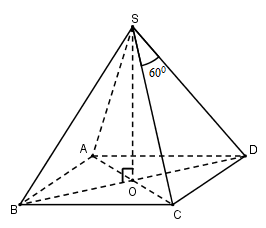
Gọi \(O = AC \cap BD\).
Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Đặt \(SA = SB = SC = SD = a\)
Tam giác $SCD$ có:\(SC = SD;\widehat {CSD} = {60^0} \Rightarrow \Delta SCD\) đều\( \Rightarrow CD = SC = SD = a\)
\( \Rightarrow \) Hình vuông $ABCD$ cạnh \(a \Rightarrow AC = BD = a\sqrt 2 \Rightarrow OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC \Rightarrow \Delta SOC\) vuông tại $O$
\( \Rightarrow SO = \sqrt {S{C^2} - O{C^2}} \Rightarrow h = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2} \Rightarrow a = h\sqrt 2 \)
\( \Rightarrow {S_{ABCD}} = {a^2} = {\left( {h\sqrt 2 } \right)^2} = 2{h^2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}h.2{h^2} = \dfrac{{2{h^3}}}{3}\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Đường thẳng \(SC\) tạo với đáy góc \({45^0}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\). Thể tích của khối chóp \(S.MCDN\) là:
-
A.
\(\dfrac{{5{a^3}\sqrt 2 }}{{12}}\)
-
B.
\(\dfrac{{5{a^3}\sqrt 2 }}{6}\)
-
C.
\(\dfrac{{5{a^3}\sqrt 2 }}{8}\)
-
D.
\(\dfrac{{5{a^3}\sqrt 2 }}{{24}}\)
Đáp án : D
- Chứng minh \(SA \bot \left( {ABCD} \right)\) và tính \(SA\).
- Xác định góc giữa đường thẳng \(SC\) và mặt phẳng đáy, sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Tính diện tích đáy \(MCDN\).
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).
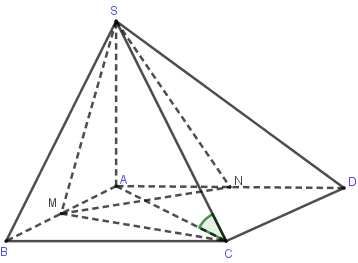
\(\left. \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {SAD} \right) = SA\end{array} \right\} \Rightarrow SA \bot \left( {ABCD} \right)\)
\( \Rightarrow AC\) là hình chiếu vuông góc của $SC$ trên \(\left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA} = {45^0}\)
(vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại \(A \Rightarrow \widehat {SCA} < {90^o}\))
\( \Rightarrow SA = AC = a\sqrt 2 \)
\(\begin{array}{l}{S_{ABCD}} = {a^2}\\{S_{AMN}} = \dfrac{1}{2}AM.AN = \dfrac{1}{2}\dfrac{a}{2}\dfrac{a}{2} = \dfrac{{{a^2}}}{8}\\{S_{BCM}} = \dfrac{1}{2}BM.BC = \dfrac{1}{2}\dfrac{a}{2}.a = \dfrac{{{a^2}}}{4}\\ \Rightarrow {S_{MCDN}} = {S_{ABCD}} - {S_{AMN}} - {S_{BCM}} = {a^2} - \dfrac{{{a^2}}}{8} - \dfrac{{{a^2}}}{4} = \dfrac{{5{a^2}}}{8}\\ \Rightarrow {V_{S.MCDN}} = \dfrac{1}{3}SA.{S_{MCDN}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{5{a^2}}}{8} = \dfrac{{5{a^3}\sqrt 2 }}{{24}}\end{array}\)
Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng \(4\) và tạo với đáy góc \({60^0}\). Thể tích của khối chóp đó là:
-
A.
\(16\)
-
B.
\(8\sqrt 3 \)
-
C.
\(48\sqrt 3 \)
-
D.
\(16\sqrt 3 \)
Đáp án : D
- Sử dụng định lí Pytago đảo chứng minh đáy là tam giác vuông, từ đó tính diện tích đáy.
- Xác định góc giữa cạnh bên và mặt đáy là góc giữa cạnh bên và hình chiếu của cạnh bên đó trên mặt đáy, từ đó sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính chiều cao của khối chóp.
- Sử dụng công thức tính thể tích khối chóp có chiều cao \(h\), diện tích đáy \(B\) là \(V = \dfrac{1}{3}Bh\).
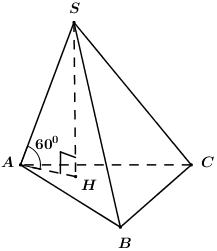
Xét tam giác \(ABC\), giả sử \(AB = 6,\,\,BC = 8,\,\,AC = 10\) ta có \(A{B^2} + B{C^2} = A{C^2}\,\,\left( { = 100} \right)\) nên tam giác \(ABC\) vuông tại \(B\) (định lí Pytago đảo) \( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.6.8 = 24\).
Gọi \(H\) là hình chiếu vuông góc của \(S\) lên \(\left( {ABC} \right)\) và giả sử \(SA\) hợp với đáy góc \({60^0}\) \( \Rightarrow HA\) là hình chiếu của \(SA\) lên \(\left( {ABC} \right)\) nên \(\angle \left( {SA;\left( {ABC} \right)} \right) = \angle \left( {SA;HA} \right) = \angle SAH = {60^0}\).
\( \Rightarrow SH = SA.\sin {60^0} = 4.\dfrac{{\sqrt 3 }}{2} = 2\sqrt 3 \).
Vậy \({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{3}.2\sqrt 3 .24 = 16\sqrt 3 \).
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. Cho \(\widehat {BAA'} = {45^0}\). Thể tích của khối lăng trụ đã cho là:
-
A.
\(\dfrac{{{a^3}\sqrt 2 }}{4}\)
-
B.
\(\dfrac{{{a^3}\sqrt 2 }}{8}\)
-
C.
\(\dfrac{{{a^3}}}{8}\)
-
D.
\(\dfrac{{{a^3}}}{4}\)
Đáp án : B
- Tính diện tích đáy và chiều cao, từ đó suy ra thể tích lăng trụ.
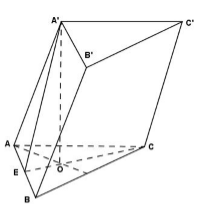
Gọi E là trung điểm của AB ta có:
\(\left\{ \begin{array}{l}OE \bot AB\\A'O \bot AB\left( {A'O \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow AB \bot \left( {A'OE} \right) \Rightarrow AB \bot A'E\)
Tam giác vuông A’EA có \(\widehat {A'AE} = {45^0} \Rightarrow \Delta EAA'\)vuông cân tại E\( \Rightarrow EA' = EA = \dfrac{a}{2};AA' = \dfrac{{a\sqrt 2 }}{2}\)
Tam giác ABC đều cạnh a nên \(CE = \dfrac{{a\sqrt 3 }}{2} \Rightarrow OE = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}\)
\(A'O \bot \left( {ABC} \right) \Rightarrow A'O \bot OE \Rightarrow \Delta A'OE\) vuông tại O
\( \Rightarrow A'O = \sqrt {A'{E^2} - O{E^2}} = \sqrt {\dfrac{{{a^2}}}{4} - \dfrac{{{a^2}}}{{12}}} = \dfrac{{a\sqrt 6 }}{6}\)
Tam giác ABC đều cạnh a nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABC.A'B'C'}} = A'O.{S_{ABC}} = \dfrac{{a\sqrt 6 }}{6}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 2 }}{8}\)
Cho hình hộp \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thoi cạnh $a\sqrt 3 ,{\mkern 1mu} BD = 3a,$ hình chiếu vuông góc của \(B\) trên mặt phẳng $\left( {A'B'C'D'} \right)$ trùng với trung điểm của \(A’C’\). Gọi $\alpha $ là góc tạo bởi hai mặt phẳng $\left( {ABCD} \right)$ và $\left( {CDD'C'} \right), \cos \alpha = \dfrac{{\sqrt {21} }}{7}$ . Thể tích của khối hộp \(ABCD.A’B’C’D\) bằng
-
A.
$\dfrac{{3{a^3}}}{4}$
-
B.
$\dfrac{{9\sqrt 3 {a^3}}}{4}$
-
C.
$\dfrac{{9{a^3}}}{4}$
-
D.
$\dfrac{{3\sqrt 3 {a^3}}}{4}$
Đáp án : C
+) Chứng minh tam giác \(A’C’D’ \) là tam giác đều.
+) Xác định góc giữa \(\left( {ABB'A'} \right)\) và \(\left( {A'B'C'D'} \right)\).
+) Gọi \(O' = A'C' \cap B'D'\) và tính \(BO’\).
+) Tính \({V_{ABCD.A'B'C'D'}} = BO'.{S_{A'B'C'D'}}\)
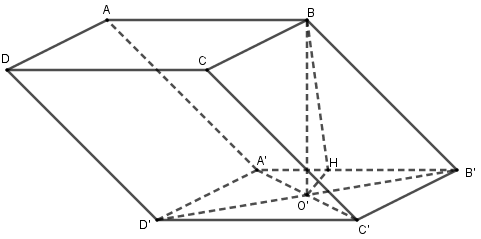
Gọi \(O'\) là trung điểm của \(A'C'\) ta có \(BO' \bot \left( {A'B'C'D'} \right)\)
Dễ thấy \(\left( {ABCD} \right)//\left( {A'B'C'D'} \right)\) và \(\left( {CDD'C'} \right)//\left( {ABB'A'} \right)\) nên góc giữa hai mặt phẳng \(\left( {CDD'C'} \right)\) và \(\left( {ABCD} \right)\) bằng góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {A'B'C'D'} \right)\).
Xét tam giác \(ABD\) có :
\(\cos \widehat {BAD} = \dfrac{{A{B^2} + A{D^2} - B{D^2}}}{{2.AB.AD}}\)\( = \dfrac{{3{a^2} + 3{a^2} - 9{a^2}}}{{2.a\sqrt 3 .a\sqrt 3 }} = - \dfrac{1}{2}\)
\( \Leftrightarrow \widehat {BAD} = {120^0}\) \( \Rightarrow \widehat {ADC} = {60^0}\)
\( \Rightarrow \Delta ACD\) đều, do đó \( \Rightarrow \Delta A'C'D'\) đều cạnh \(a\sqrt 3 \)
\( \Rightarrow {S_{A'C'D'}} = \dfrac{{{{\left( {a\sqrt 3 } \right)}^2}\sqrt 3 }}{4} = \dfrac{{3{a^2}\sqrt 3 }}{4}\) \( \Rightarrow {S_{A'B'C'D'}} = 2{S_{A'C'D'}} = \dfrac{{3{a^2}\sqrt 3 }}{2}\)
Kẻ \(O'H \bot A'B'\) thì \(A'B' \bot \left( {BO'H} \right)\) \( \Rightarrow A'B' \bot BH\).
Suy ra góc giữa \(\left( {A'B'C'D'} \right)\) và \(\left( {A'B'BA} \right)\) bằng \(\widehat {\left( {BH,O'H} \right)} = \widehat {BHO'} = \alpha \)
Mà \(\cos \alpha = \dfrac{{\sqrt {21} }}{7}\) nên \(\tan \alpha = \dfrac{2}{{\sqrt 3 }}\) \( \Rightarrow BO' = O'H\tan \alpha = \dfrac{{2O'H}}{{\sqrt 3 }}\)
Lại có \(O'H = A'O'\sin {60^0} = \dfrac{{A'C'}}{2}.\sin {60^0}\) \( = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{3a}}{4}\) \( \Rightarrow BO' = \dfrac{{2.\dfrac{{3a}}{4}}}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{2}\).
Vậy \({V_{ABCD.A'B'C'D'}} = {S_{A'B'C'D'}}.BO'\) \( = \dfrac{{3{a^2}\sqrt 3 }}{2}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{9{a^3}}}{4}\)
Cho lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $a$, và \(A'A = A'B = A'C = a\sqrt {\dfrac{7}{{12}}} \) . Thể tích khối lăng trụ \(ABC.A'B'C'\) theo $a$ là:
-
A.
\(\dfrac{{{a^3}}}{8}\)
-
B.
\(\dfrac{{{a^3}\sqrt 3 }}{8}\)
-
C.
\(\dfrac{{3{a^3}\sqrt 3 }}{8}\)
-
D.
\(\dfrac{{{a^3}\sqrt 3 }}{4}\)
Đáp án : B
- Tính diện tích đáy \({S_{ABC}}\).
- Xác định chiều cao của khối lăng trụ dựa vào tính chất của hình chóp đều.
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\) với \(S\) là diện tích đáy và \(h\) là chiều cao.
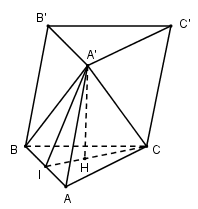
Gọi $H$ là tâm tam giác đều $ABC$ . Vì $A'A = A'B = A'C$ nên hình chóp $A'.ABC$ là đều nên \(A'H \bot \left( {ABC} \right)\)
Gọi $I$ là trung điểm của $AB$.
Vì tam giác $ABC$ đều cạnh $a$ nên \(CI = \dfrac{{a\sqrt 3 }}{2} \Rightarrow HI = \dfrac{1}{3}CI = \dfrac{{a\sqrt 3 }}{6}\)
Tam giác $A'AB$ cân tại $A'$ nên \(A'I \bot AB \Rightarrow \Delta A'AI\) vuông tại \(I \Rightarrow A'I = \sqrt {AA{'^2} - A{I^2}} = \sqrt {\dfrac{{7{a^2}}}{{12}} - \dfrac{{{a^2}}}{4}} = \dfrac{a}{{\sqrt 3 }}\)
\(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot HI \Rightarrow \Delta A'HI\) vuông tại \(H \Rightarrow A'H = \sqrt {A'{I^2} - H{I^2}} = \sqrt {\dfrac{{{a^2}}}{3} - \dfrac{{{a^2}}}{{12}}} = \dfrac{a}{2}\)
Vì tam giác $ABC$ đều cạnh $a$ nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}\)
Cho tứ diện \(ABCD\) có \(G\) là điểm thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Mặt phẳng thay đổi chứa \(BG\) và cắt \(AC,\,\,AD\) lần lượt tại \(M\) và \(N\). Giá trị nhỏ nhất của tỉ số \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}}\) là
-
A.
\(\dfrac{3}{8}\)
-
B.
\(\dfrac{4}{9}\)
-
C.
\(\dfrac{1}{2}\)
-
D.
\(\dfrac{5}{9}\)
Đáp án : B
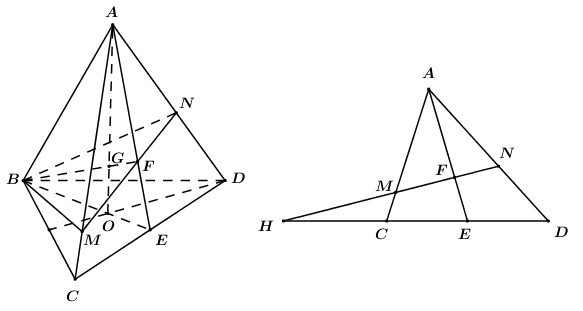
Gọi \(O\) là trọng tâm tam giác \(BCD\)
\(\begin{array}{l} \Rightarrow \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 3\overrightarrow {GO} \\ \Rightarrow \overrightarrow {GA} + 3\overrightarrow {GO} = \overrightarrow 0 \\ \Rightarrow \overrightarrow {GA} = - 3\overrightarrow {GO} \\ \Rightarrow \dfrac{{AG}}{{AO}} = \dfrac{3}{4}\end{array}\)
Trong \(\left( {ABE} \right)\) gọi \(F = BG \cap AE\,\,\left( {F \in AE} \right)\).
Lấy \(M \in AC\), trong \(\left( {ACD} \right)\) gọi \(N = MF \cap AD\,\,\,\left( {N \in AD} \right)\), khi đó ta có mặt phẳng chứa \(BG\) cắt \(AC,\,\,AD\) lần lượt tại \(M,\,\,N\) chính là \(\left( {BMN} \right)\).
Áp dụng định lí Menelaus trong tam giác \(AOE\), cát tuyến \(BGF\):
\(\dfrac{{GA}}{{GO}}.\dfrac{{BO}}{{BE}}.\dfrac{{FE}}{{FA}} = 1 \Rightarrow 3.\dfrac{2}{3}.\dfrac{{FE}}{{FA}} = 1 \Rightarrow \dfrac{{FE}}{{FA}} = \dfrac{1}{2}\) \( \Rightarrow \dfrac{{AF}}{{AE}} = \dfrac{2}{3}\) \( \Rightarrow F\) là trọng tâm tam giác \(ACD\).
Trong \(\left( {ACD} \right)\) kéo dài \(MN\) cắt \(CD\) tại \(H\). Đặt \(\dfrac{{AM}}{{AC}} = x\) \(\left( {0 < x < 1} \right)\).
Áp dụng định lí Menelaus trong tam giác \(ACE\), cát tuyến \(MHF\):
\(\dfrac{{MA}}{{MC}}.\dfrac{{HC}}{{HE}}.\dfrac{{FE}}{{FA}} = 1 \Rightarrow \dfrac{x}{{1 - x}}.\dfrac{{HC}}{{HE}}.\dfrac{1}{2} = 1\)\( \Rightarrow \dfrac{{HC}}{{HE}} = \dfrac{{2\left( {1 - x} \right)}}{x}\)
\(\begin{array}{l} \Rightarrow HE = \dfrac{x}{{2\left( {1 - x} \right)}}HC\\ \Rightarrow HC + CE = \dfrac{x}{{2\left( {1 - x} \right)}}HC\\ \Rightarrow CE = \dfrac{{3x - 2}}{{2\left( {1 - x} \right)}}HC\end{array}\)
Ta có:
\(\begin{array}{l}HD = HC + 2CE\\\,\,\,\,\,\,\,\,\, = HC + \dfrac{{3x - 2}}{{1 - x}}HC = \dfrac{{2x - 1}}{{1 - x}}HC\\ \Rightarrow \dfrac{{HE}}{{HD}} = \dfrac{x}{{2\left( {1 - x} \right)}}:\dfrac{{2x - 1}}{{1 - x}} = \dfrac{x}{{2\left( {2x - 1} \right)}}\end{array}\)
Áp dụng định lí Menelaus trong tam giác \(AED\), cát tuyến \(MFN\):
\(\begin{array}{l}\dfrac{{FA}}{{FE}}.\dfrac{{HE}}{{HD}}.\dfrac{{ND}}{{NA}} = 1 \Rightarrow 2.\dfrac{x}{{2\left( {2x - 1} \right)}}.\dfrac{{ND}}{{NA}} = 1\\ \Rightarrow \dfrac{{ND}}{{NA}} = \dfrac{{2x - 1}}{x} \Rightarrow \dfrac{{NA}}{{ND}} = \dfrac{x}{{2x - 1}}\\ \Rightarrow \dfrac{{NA}}{{NA + ND}} = \dfrac{x}{{x + 2x - 1}} = \dfrac{x}{{3x - 1}}\\ \Rightarrow \dfrac{{AN}}{{AD}} = \dfrac{x}{{3x - 1}}\end{array}\).
Khi đó ta có \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \dfrac{{AM}}{{AC}}.\dfrac{{AN}}{{AD}} = x.\dfrac{x}{{3x - 1}} = \dfrac{{{x^2}}}{{3x - 1}}\,\,\left( {x > \dfrac{1}{3}} \right)\).
Xét hàm số \(f\left( x \right) = \dfrac{{{x^2}}}{{3x - 1}}\,\,\left( {x > \dfrac{1}{3}} \right)\) ta có \(f'\left( x \right) = \dfrac{{2x\left( {3x - 1} \right) - 3{x^2}}}{{{{\left( {3x - 1} \right)}^2}}} = \dfrac{{3{x^2} - 2x}}{{{{\left( {3x - 1} \right)}^2}}}\); \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\left( {ktm} \right)\\x = \dfrac{2}{3}\end{array} \right.\)
BBT:
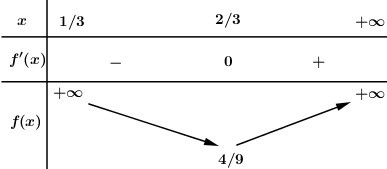
Dựa vào BBT ta thấy \(\mathop {\min }\limits_{\left( {\frac{1}{3}; + \infty } \right)} f\left( x \right) = f\left( {\dfrac{2}{3}} \right) = \dfrac{4}{9}\).
Vậy giá trị nhỏ nhất của tỉ số \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \dfrac{4}{9}\).
Đề thi THPT QG - 2021 - mã 101
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 2a,\) góc giữa hai mặt phẳng \(\left( {A'B{\rm{D}}} \right)\) và \(\left( {ABCD} \right)\) bằng \({30^0}\). Thể tích của khối hộp chữ nhật đã cho bằng
-
A.
\(6\sqrt 3 \,{a^3}.\)
-
B.
\(\dfrac{{2\sqrt 3 }}{9}{a^3}.\)
-
C.
\(2\sqrt 3 {a^3}.\)
-
D.
\(\dfrac{{2\sqrt 3 }}{3}{a^3}.\)
Đáp án : D
- Xác định góc giữa hai mặt phẳng là góc tạo bởi 2 đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Sử dụng tính chất hình vuông và tỉ số lượng giác trong tam giác vuông để tính chiều cao \(AA'\).
- Tính thể tích khối lăng trụ.
* Xác định \(\angle \left( {\left( {A'BD} \right);\left( {ABCD} \right)} \right)\).
+ \(\left( {A'BC} \right) \cap \left( {ABCD} \right) = BD\).
+ \(\left\{ \begin{array}{l}AA' \bot BD\\AO \bot BD\end{array} \right. \Rightarrow \left( {A'AO} \right) \bot BD\).
+ \(\left\{ \begin{array}{l}\left( {A'AO} \right) \cap \left( {A'BD} \right) = A'O\\\left( {A'AO} \right) \cap \left( {ABCD} \right) = AO\end{array} \right.\)
\( \Rightarrow \angle \left( {\left( {A'BD} \right);\left( {ABCD} \right)} \right) = \angle \left( {A'O;AO} \right) = \angle A'OA\).
\( \Rightarrow \angle A'OA = {30^0}\).
* Xét tam giác \(A'OA\) vuông tại \(A\) có \(AO = \dfrac{1}{2}AC = \dfrac{1}{2}BD = a\).
\( \Rightarrow AA' = \tan {30^0}.AO = \dfrac{{a\sqrt 3 }}{3}\).
\( \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABCD}}.AA' = \dfrac{1}{2}AC.BD.AA'\) \( = \dfrac{1}{2}.{\left( {2a} \right)^2}.\dfrac{{a\sqrt 3 }}{3} = \dfrac{{2\sqrt 3 {a^3}}}{3}\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\)
-
A.
\(3\)
-
B.
\(2\sqrt 2 \)
-
C.
\(2\sqrt 3 \)
-
D.
\(4\)
Đáp án : A
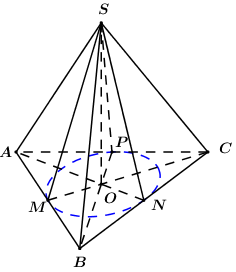
Gọi \(M,\,\,N,\,\,P\) lần lượt là hình chiếu của điểm \(S\) lên \(AB,\,\,BC,\,\,AC\) ta có:
\(\begin{array}{l}\,\,\,\,\,{S_{\Delta ABC}} = {S_{\Delta BCA}} = {S_{\Delta CAB}}\\ \Rightarrow \dfrac{1}{2}SM.AB = \dfrac{1}{2}SN.BC = \dfrac{1}{2}SP.CA\end{array}\)
Mà \(AB = BC = CA\,\,\left( {gt} \right) \Rightarrow SM = SN = SP\).
Gọi \(O\) là hình chiếu của \(S\) lên \(\left( {ABC} \right)\), ta có: \(\left\{ \begin{array}{l}AB \bot SM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot OM\).
CMTT ta có \(ON \bot BC,\,\,OP \bot AC\).
Xét các tam giác vuông \(\Delta SOM,\,\,\Delta SON,\,\,\Delta SOP\) có:
\(\begin{array}{l}SO\,\,chung\\SM = SN = SP\,\,\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta SOM = \Delta SON = \Delta SOP\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow OM = ON = OP\), suy ra \(O\) cách đều các cạnh \(AB,\,\,BC,\,\,CA\) nên \(O\) là tâm đường tròn nội tiếp \(\Delta ABC\) hoặc \(O\) là tâm đường tròn bàng tiếp \(\Delta ABC\).
+ TH1: \(O\) là tâm đường tròn nội tiếp \(\Delta ABC\). Mà \(\Delta ABC\) đều nên \(O\) là đồng thời là trọng tâm tam giác đều \(ABC\). Khi đó ta có \(AN = \dfrac{{\sqrt 6 .\sqrt 3 }}{2} = \dfrac{{3\sqrt 2 }}{2},\,\,AO = \dfrac{2}{3}AN = \sqrt 2 \).
\( \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {18 - 2} = 4\).
\({S_{\Delta ABC}} = {\left( {\sqrt 6 } \right)^2}.\dfrac{{\sqrt 3 }}{4} = \dfrac{{3\sqrt 3 }}{2}\).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SO.{S_{\Delta ABC}} = \dfrac{1}{3}.4.\dfrac{{3\sqrt 3 }}{2} = 2\sqrt 3 \).
TH2: \(O\) là tâm đường tròn bàng tiếp \(\Delta ABC\).
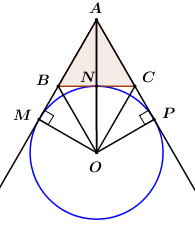
Gọi \(R\) là bán kính đường tròn bàng tiếp tam giác \(ABC\), \(p\) là nửa chu vi tam giác \(ABC\) \( \Rightarrow p = \dfrac{{3\sqrt 6 }}{2}\).
Khi đó ta có \({S_{ABC}} = \left( {p - BC} \right).R\) \( \Rightarrow {\left( {\sqrt 6 } \right)^2}.\dfrac{{\sqrt 3 }}{4} = \left( {\dfrac{{3\sqrt 6 }}{2} - \sqrt 6 } \right).R \Leftrightarrow R = \dfrac{{3\sqrt 2 }}{2}\).
Có \(AN = \dfrac{{\sqrt 6 .\sqrt 3 }}{2} = \dfrac{{3\sqrt 2 }}{2}\) \( \Rightarrow OA = AN + ON = 3\sqrt 2 \).
\( \Rightarrow SA > OA = 3\sqrt 2 \) (quan hệ giữa đường vuông góc và đường xiên)
\( \Rightarrow SB = 3\sqrt 2 \).
Áp dụng định lí Pytago trong tam giác vuông \(OBM\) có: \(OB = \sqrt {O{M^2} + B{M^2}} = \sqrt {{{\left( {\dfrac{{3\sqrt 2 }}{2}} \right)}^2} + {{\left( {\dfrac{{\sqrt 6 }}{2}} \right)}^2}} = \sqrt 6 \).
Áp dụng định lí Pytago trong tam giác vuông \(SOB\) có: \(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {{{\left( {3\sqrt 2 } \right)}^2} - {{\left( {\sqrt 6 } \right)}^2}} = 2\sqrt 3 \).
Khi đó ta có \({V_{S.ABC}} = \dfrac{1}{3}.SO.{S_{ABC}} = \dfrac{1}{3}.2\sqrt 3 .{\left( {\sqrt 6 } \right)^2}.\dfrac{{\sqrt 3 }}{4} = 3\).
Vậy \(\min {V_{S.ABC}} = 3\).
















