-
Đề kiểm tra 15 phút
-
Đề kiểm tra 15 phút - Chương I - Giải Tích 12
-
Đề kiểm tra 15 phút - Chương II - Giải Tích 12
-
Đề kiểm tra 15 phút - Chương III - Giải Tích 12
-
Đề kiểm tra 15 phút – Chương IV – Giải tích 12
-
Đề kiểm tra 15 phút - Chương I - Hình học 12
-
Đề kiểm tra 15 phút - Chương II - Hình học 12
-
Đề kiểm tra 15 phút - Chương III - Hình học 12
-
-
Đề kiểm tra 1 tiết
-
Đề kiểm tra 45 phút (1 tiết) - Chương I - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương II - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương III - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương IV - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương I - Hình học 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương II - Hình học 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương III - Hình học 12
-
-
Đề thi giữa học kì 1
-
Đề thi học kì 1
-
Đề thi giữa học kì 2
-
Đề thi học kì 2
-
ĐỀ THI THỬ THPT QUỐC GIA MÔN TOÁN
Đề kiểm tra 1 tiết Toán 12 chương 3: Nguyên hàm - Đề số 2
Đề bài
Họ nguyên hàm của hàm số \(f\left( x \right)=2x+\sin 2x\) là:
-
A.
\({{x}^{2}}-\dfrac{1}{2}\cos 2x+C\)
-
B.
\({{x}^{2}}+\dfrac{1}{2}\cos 2x+C\)
-
C.
\({{x}^{2}}-2x\cos 2x+C\)
-
D.
\({{x}^{2}}+2\cos 2x+C\)
Nếu \(f\left( 1 \right) = 12,f'\left( x \right)\) liên tục và \(\int\limits_1^4 {f'\left( x \right)dx} = 17\) thì giá trị của \(f\left( 4 \right)\) bằng:
-
A.
\(29\)
-
B.
\(5\)
-
C.
\(19\)
-
D.
\(40\)
Chọn mệnh đề đúng:
-
A.
\(\int {0dx} = C\)
-
B.
\(\int {dx} = C\)
-
C.
\(\int {dx} = 0\)
-
D.
\(\int {0dx} = x + C\)
Cho hàm số $f\left( x \right)$liên tục trên $R$ và $\int\limits_{ - 2}^4 {f\left( x \right)} dx{\rm{ = 2}}$ . Mệnh đề nào sau đây là sai?
-
A.
$\int\limits_{ - 1}^2 {f\left( {2x} \right)} d{\rm{x = 2}}$
-
B.
$\int\limits_{ - 3}^3 {f\left( {x + 1} \right)} d{\rm{x = 2}}$
-
C.
$\int\limits_{ - 1}^2 {f\left( {2x} \right)} d{\rm{x = 1}}$
-
D.
$\int\limits_0^6 {\dfrac{1}{2}f\left( {x - 2} \right)} d{\rm{x = 1}}$
Hàm số nào không là nguyên hàm của hàm số \(y = 3{x^4}\)?
-
A.
\(y = 12{x^3}\)
-
B.
\(y = \dfrac{{3{x^5}}}{5} - 1\)
-
C.
\(y = \dfrac{{3{x^5} + 1}}{5}\)
-
D.
\(y = \dfrac{3}{5}{x^5} - \dfrac{3}{5}\)
Biết \(F\left( x \right)\) là một nguyên hàm của hàm số\(f\left( x \right) = \dfrac{x}{{\sqrt {8 - {x^2}} }}\) thoả mãn \(F\left( 2 \right) = 0\). Khi đó phương trình \(F\left( x \right) = x\) có nghiệm là
-
A.
\(x = 1 - \sqrt 3 \).
-
B.
\(x = 1\).
-
C.
\(x = - 1\).
-
D.
\(x = 0\).
Cho hàm số \(y = f\left( x \right)\) là hàm số chẵn trên \(\mathbb{R}\) và \(a\) là một số thực dương. Chọn kết luận đúng:
-
A.
\(\int\limits_{ - a}^a {f\left( x \right)dx} = 0\)
-
B.
\(\int\limits_{ - a}^a {f\left( x \right)dx} = 2a\)
-
C.
\(\int\limits_{ - a}^a {f\left( x \right)dx} = 2\int\limits_0^a {f\left( x \right)dx} \)
-
D.
\(\int\limits_{ - a}^a {f\left( x \right)dx} = \int\limits_{ - a}^0 {f\left( x \right)dx} \)
Cho hai hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và có đồ thị như hình vẽ bên. Gọi $S$ là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng \(x = a,x = b\). Thể tích $V$ của vật thể tròn xoay tạo thành khi quay $S$ quanh trục $Ox$ được tính bởi công thức nào sau đây ?
-
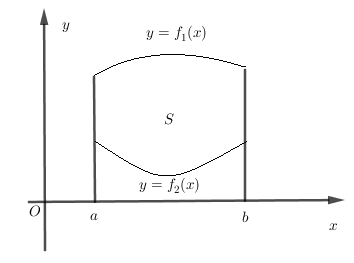
A.
\(V = \pi \int\limits_a^b {\left( {f_1^2(x) - f_2^2(x)} \right)} dx\).
-
B.
\(V = \pi \int\limits_a^b {\left( {{f_1}(x) - {f_2}(x)} \right)} dx\).
-
C.
\(V = \int\limits_a^b {\left( {f_1^2(x) - f_2^2(x)} \right)} dx\).
-
D.
\(V = \pi \int\limits_a^b {{{\left( {{f_1}(x) - {f_2}(x)} \right)}^2}} dx\).
Cho hai hàm số \(f,\,\,g\) liên tục trên đoạn $\left[ {a;b} \right]$ và số thực $k$ tùy ý. Trong các khẳng định sau, khẳng định nào sai ?
-
A.
$\int\limits_a^b {kf\left( x \right)dx} {\rm{\;}} = k\int\limits_a^b {f\left( x \right)dx} $
-
B.
$\int\limits_a^b {xf\left( x \right)dx} {\rm{\;}} = x\int\limits_a^b {f\left( x \right)dx} $
-
C.
$\int\limits_a^b {f\left( x \right)dx} {\rm{\;}} = {\rm{\;}} - \int\limits_b^a {f\left( x \right)dx} $
-
D.
$\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} {\rm{\;}} = \int\limits_a^b {f\left( x \right)dx} {\rm{\;}} + \int\limits_a^b {g\left( x \right)dx} $
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y = {x^3} - x;y = 2x$ và các đường thẳng $x = - 1;x = 1$ được xác định bởi công thức:
-
A.
$S = \left| {\int_{ - 1}^1 {\left( {3x - {x^3}} \right)dx} } \right|$
-
B.
$S = \int_{ - 1}^0 {\left( {3x - {x^3}} \right)dx} + \int_0^1 {\left( {{x^3} - 3x} \right)dx} $
-
C.
$S = \int_{ - 1}^1 {\left( {3x - {x^3}} \right)dx} $
-
D.
$S = \int_{ - 1}^0 {\left( {{x^3} - 3x} \right)dx} + \int_0^1 {\left( {3x - {x^3}} \right)dx} $
Tích phân \(I = \int\limits_1^2 {{x^5}} dx\) có giá trị là:
-
A.
\(\frac{{19}}{3}\).
-
B.
\(\frac{{32}}{3}\).
-
C.
\(\frac{{16}}{3}\).
-
D.
\(\frac{{21}}{2}\).
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {x^2} - 1\), trục hoành và hai đường thẳng \(x = - 1;x = - 3\) là:
-
A.
\(S = \int\limits_{ - 3}^{ - 1} {\left| {{x^2} - 1} \right|dx} \)
-
B.
\(S = \int\limits_{ - 1}^{ - 3} {\left| {{x^2} - 1} \right|dx} \)
-
C.
\(S = \int\limits_{ - 3}^0 {\left| {{x^2} - 1} \right|dx} \)
-
D.
\(S = \int\limits_{ - 3}^{ - 1} {\left( {1 - {x^2}} \right)dx} \)
Nếu \(t = u\left( x \right)\) thì:
-
A.
\(dt = u'\left( x \right)dx\)
-
B.
\(dx = u'\left( t \right)dt\)
-
C.
\(dt = \dfrac{1}{{u\left( x \right)}}dx\)
-
D.
\(dx = \dfrac{1}{{u\left( t \right)}}dt\)
Biết $\int {f\left( x \right){\mkern 1mu} {\rm{d}}x = 2x\ln \left( {3x - 1} \right) + C} $ với $x \in \left( {\dfrac{1}{9}; + \infty } \right)$. Tìm khẳng định đúng trong các khẳng định sau.
-
A.
$\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x = 2x\ln \left( {9x - 1} \right) + C.} $
-
B.
$\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x = 6x\ln \left( {3x - 1} \right) + C.} $
-
C.
$\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x = 6x\ln \left( {9x - 1} \right) + C.} $
-
D.
$\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x = 3x\ln \left( {9x - 1} \right) + C.} $
Cho hàm số \(y=f\left( x \right)\) liên tục và có đồ thị như hình bên. Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục \(Ox.\) Quay hình phẳng \(D\) quanh trục \(Ox\) ta được khối tròn xoay có thể tích \(V\) được xác định theo công thức
-
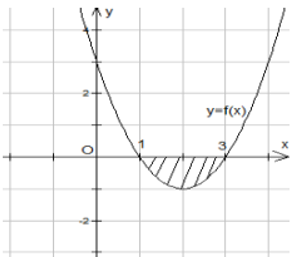
A.
\(V={{\pi }^{2}}\int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
-
B.
\(V=\int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
-
C.
\(V=\frac{1}{3}\int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
-
D.
\(V=\pi \int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
Cho hàm số \(f\left( x \right) = {e^{ - 2018x + 2017}}\). Gọi \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) mà \(F\left( 1 \right) = e\). Chọn mệnh đề đúng:
-
A.
\(F\left( x \right) = - \dfrac{1}{{2018}}{e^{ - 2018x + 2017}} + \dfrac{1}{{2018e}}\)
-
B.
\(F\left( x \right) = - \dfrac{1}{{2018}}{e^{ - 2018x + 2017}} + e + \dfrac{1}{{2018e}}\)
-
C.
\(F\left( x \right) = - 2018{e^{ - 2018x + 2017}} + e + \dfrac{{2018}}{e}\)
-
D.
\(F\left( x \right) = - 2018{e^{ - 2018x + 2017}} + \dfrac{1}{{2018e}}\)
Cho nguyên hàm \(\int {x\sin xdx} \). Nếu đặt \(\left\{ \begin{array}{l}u = x\\dv = \sin xdx\end{array} \right.\) thì:
-
A.
\(\int {x\sin xdx} = x\sin x - \int {\cos xdx} \)
-
B.
\(\int {x\sin xdx} = - x\cos x + \int {\cos xdx} \)
-
C.
\(\int {x\sin xdx} = x\cos x - \int {\cos xdx} \)
-
D.
\(\int {x\sin xdx} = x\cos x - \int {\sin xdx} \)
Cho \(F(x) = - \dfrac{1}{{3{x^3}}}\) là một nguyên hàm của hàm số \(\dfrac{{f(x)}}{x}\). Tìm nguyên hàm của hàm số \(f'(x)\ln x\).
-
A.
\(\int {f'(x)\ln xdx = - \dfrac{{\ln x}}{{{x^3}}} + \dfrac{1}{{3{x^3}}} + C} \).
-
B.
\(\int {f'(x)\ln xdx = \dfrac{{\ln x}}{{{x^3}}} - \dfrac{1}{{5{x^5}}} + C} \).
-
C.
\(\int {f'(x)\ln xdx = \dfrac{{\ln x}}{{{x^3}}} + \dfrac{1}{{3{x^3}}} + C} \).
-
D.
\(\int {f'(x)\ln xdx = \dfrac{{\ln x}}{{{x^3}}} + \dfrac{1}{{5{x^5}}} + C} \).
Nếu \(\int\limits_{ - 2}^0 {\left( {4 - {e^{ -{\frac{x}{2}}}}} \right)dx} = K - 2e\) thì giá trị của \(K\) là
-
A.
\(12,5\).
-
B.
\(9\).
-
C.
\(11\).
-
D.
\(10\).
Kết quả tích phân \(I = \int\limits_1^e {\dfrac{{\ln x}}{{x\left( {{{\ln }^2}x + 1} \right)}}dx} \) có dạng \(I = a\ln 2 + b\) với \(a,b \in Q\) . Khẳng định nào sau đây là đúng?
-
A.
$2a + b = 1$
-
B.
\({a^2} + {b^2} = 4\)
-
C.
\(a - b = 1\)
-
D.
\(ab = \dfrac{1}{2}\)
Gọi \(S\) là diện tích hình phẳng \(\left( H \right)\) giới hạn bởi các đường $y=f\left( x \right),~$trục hoành và hai đường thẳng \(x = - 1,x = 2\) (như hình vẽ). Đặt $a=\underset{-1}{\overset{0}{\mathop \int }}\,f\left( x \right)dx,~b=\underset{0}{\overset{2}{\mathop \int }}\,f\left( x \right)dx.$ Mệnh đề nào sau đây đúng?
-
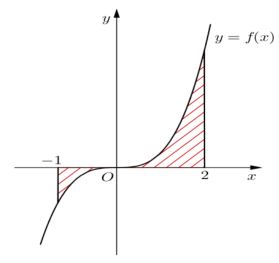
A.
\(S = b - a.\)
-
B.
\(S = b + a.\)
-
C.
\(S = - b + a.\)
-
D.
\(S = - b - a.\)
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=x{{e}^{x}},\ \ y=0,\ x=0,\ x=1\) xung quanh trục \(Ox\) là:
-
A.
\(V=\int\limits_{0}^{1}{{{x}^{2}}{{e}^{2x}}dx.}\)
-
B.
\(V=\pi \int\limits_{0}^{1}{x{{e}^{x}}dx.}\)
-
C.
\(V=\pi \int\limits_{0}^{1}{{{x}^{2}}{{e}^{2x}}dx.}\)
-
D.
\(V=\pi \int\limits_{0}^{1}{{{x}^{2}}{{e}^{x}}dx.}\)
Biết \(\int\limits_{0}^{1}{\frac{\pi {{x}^{3}}+{{2}^{x}}+\text{e}{{x}^{3}}{{.2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{m}+\frac{1}{\text{e}\ln n}\ln \left( p+\frac{\text{e}}{\text{e}+\pi } \right)\) với \(m\), \(n\), \(p\) là các số nguyên dương. Tính tổng \(S=m+n+p\).
-
A.
\(S=6\).
-
B.
\(S=5\).
-
C.
\(S=7\).
-
D.
\(S=8\).
Tìm thể tích \(V\) của vật tròn xoay sinh ra bởi đường tròn \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\) khi quay quanh trục \(Ox.\)
-
A.
\(V=24{{\pi }^{2}}.\)
-
B.
\(V=24\pi .\)
-
C.
\(V=16\pi .\)
-
D.
\(V=36{{\pi }^{2}}.\)
Cho tích phân $I = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}{\rm{d}}x} = \dfrac{{m - \pi }}{{m + \pi }}$, giá trị của $m$ bằng :
-
A.
$2$.
-
B.
$7$.
-
C.
$4$.
-
D.
$5$.
Lời giải và đáp án
Họ nguyên hàm của hàm số \(f\left( x \right)=2x+\sin 2x\) là:
-
A.
\({{x}^{2}}-\dfrac{1}{2}\cos 2x+C\)
-
B.
\({{x}^{2}}+\dfrac{1}{2}\cos 2x+C\)
-
C.
\({{x}^{2}}-2x\cos 2x+C\)
-
D.
\({{x}^{2}}+2\cos 2x+C\)
Đáp án : A
\(f\left( x \right)=2x+\sin 2x \) \(\Rightarrow F\left( x \right)=\int{f\left( x \right)dx}=\int{\left( 2x+\sin 2x \right)dx}\) \(={{x}^{2}}-\dfrac{1}{2}\cos 2x+C\)
Nếu \(f\left( 1 \right) = 12,f'\left( x \right)\) liên tục và \(\int\limits_1^4 {f'\left( x \right)dx} = 17\) thì giá trị của \(f\left( 4 \right)\) bằng:
-
A.
\(29\)
-
B.
\(5\)
-
C.
\(19\)
-
D.
\(40\)
Đáp án : A
- Sử dụng định nghĩa tích phân $I = \int\limits_a^b {f\left( x \right)dx} = \left. {F\left( x \right)} \right|_a^b = F\left( b \right) - F\left( a \right)$
- Tính chất nguyên hàm: \(\int {f'\left( x \right)dx} = f\left( x \right) + C\).
Ta có: \(\int\limits_1^4 {f'\left( x \right)dx} = 17 \Rightarrow \left. {f\left( x \right)} \right|_1^4 = 17 \Rightarrow f\left( 4 \right) - f\left( 1 \right) = 17 \Rightarrow f\left( 4 \right) - 12 = 17 \Rightarrow f\left( 4 \right) = 29\)
Chọn mệnh đề đúng:
-
A.
\(\int {0dx} = C\)
-
B.
\(\int {dx} = C\)
-
C.
\(\int {dx} = 0\)
-
D.
\(\int {0dx} = x + C\)
Đáp án : A
Ta có: \(\int {0dx} = C\) nên A đúng, D sai.
\(\int {dx} = x+C \) nên B, C sai
Cho hàm số $f\left( x \right)$liên tục trên $R$ và $\int\limits_{ - 2}^4 {f\left( x \right)} dx{\rm{ = 2}}$ . Mệnh đề nào sau đây là sai?
-
A.
$\int\limits_{ - 1}^2 {f\left( {2x} \right)} d{\rm{x = 2}}$
-
B.
$\int\limits_{ - 3}^3 {f\left( {x + 1} \right)} d{\rm{x = 2}}$
-
C.
$\int\limits_{ - 1}^2 {f\left( {2x} \right)} d{\rm{x = 1}}$
-
D.
$\int\limits_0^6 {\dfrac{1}{2}f\left( {x - 2} \right)} d{\rm{x = 1}}$
Đáp án : A
Sử dụng phương pháp đổi biến số để tích tích phân ở các đáp án.
Dựa vào các đáp án, ta có nhận xét sau:
$\begin{array}{l}\int\limits_{ - 1}^2 {f(2x)dx} = \dfrac{1}{2}\int\limits_{ - 1}^2 {f(2x)d(2x)} = \dfrac{1}{2}\int\limits_{ - 2}^4 {f(x)dx = 1} \\\int\limits_{ - 3}^3 {f(x + 1)dx} = \int\limits_{ - 3}^3 {f(x + 1)d(x + 1)} = \int\limits_{ - 2}^4 {f(x)dx = 2} \\\int\limits_0^6 {\dfrac{1}{2}f(x - 2)dx} = \int\limits_0^6 {\dfrac{1}{2}f(x - 2)d(x - 2)} = \dfrac{1}{2}\int\limits_{ - 2}^4 {f(x)dx = 1} \end{array}$
Do đó các đáp án B, C, D đều đúng, đáp án A sai.
Hàm số nào không là nguyên hàm của hàm số \(y = 3{x^4}\)?
-
A.
\(y = 12{x^3}\)
-
B.
\(y = \dfrac{{3{x^5}}}{5} - 1\)
-
C.
\(y = \dfrac{{3{x^5} + 1}}{5}\)
-
D.
\(y = \dfrac{3}{5}{x^5} - \dfrac{3}{5}\)
Đáp án : A
\(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) nếu \(F'\left( x \right) = f\left( x \right)\).
Quan sát các đáp án ta thấy mỗi hàm số ở đáp án B, C, D đều có đạo hàm bằng \(3{x^4}\).
Chỉ có đáp án A: \(\left( {12{x^3}} \right)' = 36{x^2} \ne 3{x^4}\) nên A sai.
Biết \(F\left( x \right)\) là một nguyên hàm của hàm số\(f\left( x \right) = \dfrac{x}{{\sqrt {8 - {x^2}} }}\) thoả mãn \(F\left( 2 \right) = 0\). Khi đó phương trình \(F\left( x \right) = x\) có nghiệm là
-
A.
\(x = 1 - \sqrt 3 \).
-
B.
\(x = 1\).
-
C.
\(x = - 1\).
-
D.
\(x = 0\).
Đáp án : A
- Tìm hàm số \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) và thỏa mãn điều kiện bài cho.
- Giải phương trình và kết luận nghiệm.
Đặt \(t = \sqrt {8 - {x^2}} \Rightarrow {t^2} = 8 - {x^2} \Rightarrow - tdt = xdx\)
\(\int {\dfrac{x}{{\sqrt {8 - {x^2}} }}dx = - \int {\dfrac{{tdt}}{t} = - t + C = - \sqrt {8 - {x^2}} + C} } \)
Vì \(F\left( 2 \right) = 0\) nên \(C = 2\)
Ta có phương trình $ - \sqrt {8 - {x^2}} + 2 = x \Leftrightarrow x = 1 - \sqrt 3 $
Cho hàm số \(y = f\left( x \right)\) là hàm số chẵn trên \(\mathbb{R}\) và \(a\) là một số thực dương. Chọn kết luận đúng:
-
A.
\(\int\limits_{ - a}^a {f\left( x \right)dx} = 0\)
-
B.
\(\int\limits_{ - a}^a {f\left( x \right)dx} = 2a\)
-
C.
\(\int\limits_{ - a}^a {f\left( x \right)dx} = 2\int\limits_0^a {f\left( x \right)dx} \)
-
D.
\(\int\limits_{ - a}^a {f\left( x \right)dx} = \int\limits_{ - a}^0 {f\left( x \right)dx} \)
Đáp án : C
Đổi biến \(x = - t\) và tính tích phân \(\int\limits_{ - a}^a {f\left( x \right)dx} \)
\(\int\limits_{ - a}^a {f\left( x \right)dx} = \int\limits_{ - a}^0 {f\left( x \right)dx} + \int\limits_0^a {f\left( x \right)dx} \)
Đặt \(x = - t\) thì \(dx = - dt\) \( \Rightarrow \int\limits_{ - a}^0 {f\left( x \right)dx} = \int\limits_a^0 {f\left( { - t} \right)\left( { - dt} \right)} = \int\limits_0^a {f\left( { - t} \right)dt} \)
Mà \(f\left( x \right)\) là hàm chẵn nên \(f\left( { - t} \right) = f\left( t \right)\) hay \(\int\limits_0^a {f\left( { - t} \right)dt} = \int\limits_0^a {f\left( t \right)dt} = \int\limits_0^a {f\left( x \right)dx} \)
Do đó \(\int\limits_{ - a}^0 {f\left( x \right)dx} = \int\limits_0^a {f\left( x \right)dx} \) \( \Rightarrow \int\limits_{ - a}^a {f\left( x \right)dx} = \int\limits_{ - a}^0 {f\left( x \right)dx} + \int\limits_0^a {f\left( x \right)dx} = 2\int\limits_0^a {f\left( x \right)dx} \)
Cho hai hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và có đồ thị như hình vẽ bên. Gọi $S$ là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng \(x = a,x = b\). Thể tích $V$ của vật thể tròn xoay tạo thành khi quay $S$ quanh trục $Ox$ được tính bởi công thức nào sau đây ?
-
A.
\(V = \pi \int\limits_a^b {\left( {f_1^2(x) - f_2^2(x)} \right)} dx\).
-
B.
\(V = \pi \int\limits_a^b {\left( {{f_1}(x) - {f_2}(x)} \right)} dx\).
-
C.
\(V = \int\limits_a^b {\left( {f_1^2(x) - f_2^2(x)} \right)} dx\).
-
D.
\(V = \pi \int\limits_a^b {{{\left( {{f_1}(x) - {f_2}(x)} \right)}^2}} dx\).
Đáp án : A
Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng \(\left( H \right)\) giới hạn bởi các đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) liên tục trên \(\left[ {a;b} \right],0 \le f\left( x \right) \le g\left( x \right),\forall x \in \left[ {a;b} \right]\) quay quanh trục \(Ox\)
Công thức tính: \(V = \pi \int\limits_a^b {\left[ {{g^2}\left( x \right) - {f^2}\left( x \right)} \right]dx} \)
Theo công thức trên ta có: \(V = \pi \int\limits_a^b {\left( {f_1^2(x) - f_2^2\left( x \right)} \right)} dx\) (vì đồ thị hàm số \(y = {f_1}\left( x \right)\) nằm phía trên đồ thị hàm số \(y = {f_2}\left( x \right)\).
Cho hai hàm số \(f,\,\,g\) liên tục trên đoạn $\left[ {a;b} \right]$ và số thực $k$ tùy ý. Trong các khẳng định sau, khẳng định nào sai ?
-
A.
$\int\limits_a^b {kf\left( x \right)dx} {\rm{\;}} = k\int\limits_a^b {f\left( x \right)dx} $
-
B.
$\int\limits_a^b {xf\left( x \right)dx} {\rm{\;}} = x\int\limits_a^b {f\left( x \right)dx} $
-
C.
$\int\limits_a^b {f\left( x \right)dx} {\rm{\;}} = {\rm{\;}} - \int\limits_b^a {f\left( x \right)dx} $
-
D.
$\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} {\rm{\;}} = \int\limits_a^b {f\left( x \right)dx} {\rm{\;}} + \int\limits_a^b {g\left( x \right)dx} $
Đáp án : B
Sử dụng tính chất của tích phân.
Đáp án A: đúng theo tính chất tích phân.
Đáp án B: sai vì \(x\) không phải hằng số nên không đưa được ra ngoài dấu tích phân.
Đáp án C: đúng theo tính chất tích phân.
Đáp án D: đúng theo tính chất tích phân.
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y = {x^3} - x;y = 2x$ và các đường thẳng $x = - 1;x = 1$ được xác định bởi công thức:
-
A.
$S = \left| {\int_{ - 1}^1 {\left( {3x - {x^3}} \right)dx} } \right|$
-
B.
$S = \int_{ - 1}^0 {\left( {3x - {x^3}} \right)dx} + \int_0^1 {\left( {{x^3} - 3x} \right)dx} $
-
C.
$S = \int_{ - 1}^1 {\left( {3x - {x^3}} \right)dx} $
-
D.
$S = \int_{ - 1}^0 {\left( {{x^3} - 3x} \right)dx} + \int_0^1 {\left( {3x - {x^3}} \right)dx} $
Đáp án : D
- Bước 1: Giải phương trình \(f\left( x \right) = g\left( x \right)\) tìm nghiệm.
- Bước 2: Phá dấu giá trị tuyệt đối của biểu thức \(\left| {f\left( x \right) - g\left( x \right)} \right|\)
- Bước 3: Tính diện tích hình phẳng theo công thức tích phân \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
Xét phương trình hoành độ giao điểm của 2 đồ thị:
${x^3}-x = 2x \Leftrightarrow {x^3}-3x = 0 \Leftrightarrow x = 0$ (chỉ xét trên $\left( {-1;1} \right)$)
Với $x \in \left( {-1;0} \right)$ thì ${x^3}-3x > 0$ ; với $x \in \left( {0;1} \right)$ thì ${x^3}-3x < 0$
Diện tích cần tìm là $S = \int\limits_{ - 1}^1 {\left| {{x^3} - 3x} \right|dx} = \int\limits_{ - 1}^0 {\left( {{x^3} - 3x} \right)dx} + \int\limits_0^1 {\left( {3x - {x^3}} \right)dx} $
Tích phân \(I = \int\limits_1^2 {{x^5}} dx\) có giá trị là:
-
A.
\(\frac{{19}}{3}\).
-
B.
\(\frac{{32}}{3}\).
-
C.
\(\frac{{16}}{3}\).
-
D.
\(\frac{{21}}{2}\).
Đáp án : D
Sử dụng công thức tính nguyên hàm hàm lũy thừa \(\int {{x^\alpha }dx = \dfrac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C} \)
Ta có: $I = \int\limits_1^2 {{x^5}} dx = \left. {\dfrac{{{x^6}}}{6}} \right|_1^2 = \dfrac{{21}}{2}$.
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {x^2} - 1\), trục hoành và hai đường thẳng \(x = - 1;x = - 3\) là:
-
A.
\(S = \int\limits_{ - 3}^{ - 1} {\left| {{x^2} - 1} \right|dx} \)
-
B.
\(S = \int\limits_{ - 1}^{ - 3} {\left| {{x^2} - 1} \right|dx} \)
-
C.
\(S = \int\limits_{ - 3}^0 {\left| {{x^2} - 1} \right|dx} \)
-
D.
\(S = \int\limits_{ - 3}^{ - 1} {\left( {1 - {x^2}} \right)dx} \)
Đáp án : A
Sử dụng công thức tính diện hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), đường thẳng \(y = 0\) và hai đường thẳng \(x = a,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {x^2} - 1\), trục hoành và hai đường thẳng \(x = - 1;x = - 3\) là: \(S = \int\limits_{ - 3}^{ - 1} {\left| {{x^2} - 1} \right|dx} \)
Nếu \(t = u\left( x \right)\) thì:
-
A.
\(dt = u'\left( x \right)dx\)
-
B.
\(dx = u'\left( t \right)dt\)
-
C.
\(dt = \dfrac{1}{{u\left( x \right)}}dx\)
-
D.
\(dx = \dfrac{1}{{u\left( t \right)}}dt\)
Đáp án : A
Sử dụng công thức tính vi phân $dy=y'dx$
Nếu \(t = u\left( x \right)\)thì \(dt = u'\left( x \right)dx\).
Biết $\int {f\left( x \right){\mkern 1mu} {\rm{d}}x = 2x\ln \left( {3x - 1} \right) + C} $ với $x \in \left( {\dfrac{1}{9}; + \infty } \right)$. Tìm khẳng định đúng trong các khẳng định sau.
-
A.
$\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x = 2x\ln \left( {9x - 1} \right) + C.} $
-
B.
$\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x = 6x\ln \left( {3x - 1} \right) + C.} $
-
C.
$\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x = 6x\ln \left( {9x - 1} \right) + C.} $
-
D.
$\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x = 3x\ln \left( {9x - 1} \right) + C.} $
Đáp án : A
Sử dụng công thức đổi biến $t = 3x$ để tính nguyên hàm $\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x} $.
Đặt $t = 3x \Rightarrow dt = 3dx \Rightarrow dx = \dfrac{{dt}}{3}$, khi đó:
$\begin{array}{*{20}{l}}{\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x} {\rm{\;}} = \dfrac{1}{3}\int {f\left( t \right)dt} {\rm{\;}} = \dfrac{1}{3}\left( {2t\ln \left( {3t - 1} \right)} \right) + C}\\{ = \dfrac{1}{3}\left( {2.3x.\ln \left( {3.3x - 1} \right)} \right) + C = 2x\ln \left( {9x - 1} \right) + C}\end{array}$
Vậy $\int {f\left( {3x} \right){\mkern 1mu} {\rm{d}}x} {\rm{\;}} = 2x\ln \left( {9x - 1} \right) + C$
Cho hàm số \(y=f\left( x \right)\) liên tục và có đồ thị như hình bên. Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục \(Ox.\) Quay hình phẳng \(D\) quanh trục \(Ox\) ta được khối tròn xoay có thể tích \(V\) được xác định theo công thức
-
A.
\(V={{\pi }^{2}}\int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
-
B.
\(V=\int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
-
C.
\(V=\frac{1}{3}\int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
-
D.
\(V=\pi \int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
Đáp án : D
Công thức tính thể tích của khối tròn xoay là \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\,\text{d}x}\)
Thể tích khối tròn xoay cần tính là \(V=\pi \int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
Cho hàm số \(f\left( x \right) = {e^{ - 2018x + 2017}}\). Gọi \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) mà \(F\left( 1 \right) = e\). Chọn mệnh đề đúng:
-
A.
\(F\left( x \right) = - \dfrac{1}{{2018}}{e^{ - 2018x + 2017}} + \dfrac{1}{{2018e}}\)
-
B.
\(F\left( x \right) = - \dfrac{1}{{2018}}{e^{ - 2018x + 2017}} + e + \dfrac{1}{{2018e}}\)
-
C.
\(F\left( x \right) = - 2018{e^{ - 2018x + 2017}} + e + \dfrac{{2018}}{e}\)
-
D.
\(F\left( x \right) = - 2018{e^{ - 2018x + 2017}} + \dfrac{1}{{2018e}}\)
Đáp án : B
- Tìm nguyên hàm của \(f\left( x \right)\), sử dụng công thức nguyên hàm \(\int {{e^{ax + b}}dx} = \dfrac{1}{a}{e^{ax + b}} + C\).
- Thay \(x = 1\) tìm \(C \Rightarrow F\left( x \right)\).
Ta có:
\(F\left( x \right) = \int {f\left( x \right)dx} = \int {{e^{ - 2018x + 2017}}dx} = \dfrac{1}{{ - 2018}}{e^{ - 2018x + 2017}} + C\)
Với \(x = 1\) thì \( - \dfrac{1}{{2018}}{e^{ - 1}} + C = e \Leftrightarrow C = e + \dfrac{1}{{2018}}{e^{ - 1}}\)
Vậy \(F\left( x \right) = - \dfrac{1}{{2018}}{e^{ - 2018x + 2017}} + e + \dfrac{1}{{2018e}}\).
Cho nguyên hàm \(\int {x\sin xdx} \). Nếu đặt \(\left\{ \begin{array}{l}u = x\\dv = \sin xdx\end{array} \right.\) thì:
-
A.
\(\int {x\sin xdx} = x\sin x - \int {\cos xdx} \)
-
B.
\(\int {x\sin xdx} = - x\cos x + \int {\cos xdx} \)
-
C.
\(\int {x\sin xdx} = x\cos x - \int {\cos xdx} \)
-
D.
\(\int {x\sin xdx} = x\cos x - \int {\sin xdx} \)
Đáp án : B
Sử dụng công thức nguyên hàm từng phần \(\int {udv} = uv - \int {vdu} \)
Ta có:
\(\left\{ \begin{array}{l}u = x\\dv = \sin xdx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = - \cos x\end{array} \right.\)
Khi đó \(\int {x\sin xdx} = - x\cos x + \int {\cos xdx} \)
Cho \(F(x) = - \dfrac{1}{{3{x^3}}}\) là một nguyên hàm của hàm số \(\dfrac{{f(x)}}{x}\). Tìm nguyên hàm của hàm số \(f'(x)\ln x\).
-
A.
\(\int {f'(x)\ln xdx = - \dfrac{{\ln x}}{{{x^3}}} + \dfrac{1}{{3{x^3}}} + C} \).
-
B.
\(\int {f'(x)\ln xdx = \dfrac{{\ln x}}{{{x^3}}} - \dfrac{1}{{5{x^5}}} + C} \).
-
C.
\(\int {f'(x)\ln xdx = \dfrac{{\ln x}}{{{x^3}}} + \dfrac{1}{{3{x^3}}} + C} \).
-
D.
\(\int {f'(x)\ln xdx = \dfrac{{\ln x}}{{{x^3}}} + \dfrac{1}{{5{x^5}}} + C} \).
Đáp án : C
- Tìm hàm số \(f\left( x \right)\) rồi thay vào tính nguyên hàm của hàm số \(f'\left( x \right)\ln x\).
Ta có : \(F'(x) = \dfrac{1}{3}.\dfrac{{3{x^2}}}{{{x^6}}} = \dfrac{1}{{{x^4}}} = \dfrac{{f(x)}}{x} \Rightarrow f(x) = \dfrac{1}{{{x^3}}}\).
Xét \(I = \int {f'(x)\ln xdx} \). Đặt \(\left\{ \begin{array}{l}u = \ln x\\dv = f'(x)dx\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}du = \dfrac{1}{x}dx\\v = f(x)\end{array} \right.\).
Ta có : $I = \ln x.f(x) - \int {\dfrac{{f(x)}}{x}dx + C = \dfrac{{\ln x}}{{{x^3}}} + \dfrac{1}{{3{x^3}}} + C} $.
Nếu \(\int\limits_{ - 2}^0 {\left( {4 - {e^{ -{\frac{x}{2}}}}} \right)dx} = K - 2e\) thì giá trị của \(K\) là
-
A.
\(12,5\).
-
B.
\(9\).
-
C.
\(11\).
-
D.
\(10\).
Đáp án : D
Sử dụng công thức nguyên hàm hàm số mũ \(\int {{e^{ax + b}}dx} = \dfrac{1}{a}{e^{ax + b}} + C\) và nguyên hàm hàm đa thức.
\(K = \int\limits_{ - 2}^0 {\left( {4 - {e^{-\frac{x}{2}}}} \right)dx} + 2e = \left. {\left( {4x + 2{e^{-\frac{x}{2}}}} \right)} \right|_{ - 2}^0 + 2e = 2 - \left( { - 8 + 2e} \right) + 2e = 10\)
Kết quả tích phân \(I = \int\limits_1^e {\dfrac{{\ln x}}{{x\left( {{{\ln }^2}x + 1} \right)}}dx} \) có dạng \(I = a\ln 2 + b\) với \(a,b \in Q\) . Khẳng định nào sau đây là đúng?
-
A.
$2a + b = 1$
-
B.
\({a^2} + {b^2} = 4\)
-
C.
\(a - b = 1\)
-
D.
\(ab = \dfrac{1}{2}\)
Đáp án : A
- Bước 1: Đặt \(t = u\left( x \right)\), đổi cận \(\left\{ \begin{array}{l}x = a \Rightarrow t = u\left( a \right) = a'\\x = b \Rightarrow t = u\left( b \right) = b'\end{array} \right.\) .
- Bước 2: Tính vi phân \(dt = u'\left( x \right)dx\).
- Bước 3: Biến đổi \(f\left( x \right)dx\) thành \(g\left( t \right)dt\).
- Bước 4: Tính tích phân \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_{a'}^{b'} {g\left( t \right)dt} \).
Cách 1: Đặt \(t = {\ln ^2}x + 1 \Rightarrow dt = 2\ln x\dfrac{{dx}}{x} \Rightarrow \dfrac{{\ln xdx}}{x} = \dfrac{{dt}}{2}\).
Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = 1\\x = e \Rightarrow t = 2\end{array} \right.\)
Khi đó ta có:
\(I = \dfrac{1}{2}\int\limits_1^2 {\dfrac{{dt}}{t}} = \left. {\dfrac{1}{2}\ln \left| t \right|} \right|_1^2 = \dfrac{1}{2}\ln 2 = a\ln 2 + b \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\\b = 0\end{array} \right. \Rightarrow 2a + b = 1\)
Gọi \(S\) là diện tích hình phẳng \(\left( H \right)\) giới hạn bởi các đường $y=f\left( x \right),~$trục hoành và hai đường thẳng \(x = - 1,x = 2\) (như hình vẽ). Đặt $a=\underset{-1}{\overset{0}{\mathop \int }}\,f\left( x \right)dx,~b=\underset{0}{\overset{2}{\mathop \int }}\,f\left( x \right)dx.$ Mệnh đề nào sau đây đúng?
-
A.
\(S = b - a.\)
-
B.
\(S = b + a.\)
-
C.
\(S = - b + a.\)
-
D.
\(S = - b - a.\)
Đáp án : A
- Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\) là:\(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
- Công thức tổng 2 tích phân $\int\limits_a^b {f(x)dx} + \int\limits_b^c {f(x)dx} = \int\limits_a^c {f(x)dx} $
Diện tích hình phẳng là S =\(\int\limits_{ - 1}^2 {\left| {f(x)} \right|} dx\)
Dựa vào hình vẽ ta có được: $S = \int\limits_{ - 1}^0 {(0 - f(x))dx} + \int\limits_0^2 {f(x)dx} = - \int\limits_{ - 1}^0 {f(x)dx + } \int\limits_0^2 {f(x)dx} = b - a$
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=x{{e}^{x}},\ \ y=0,\ x=0,\ x=1\) xung quanh trục \(Ox\) là:
-
A.
\(V=\int\limits_{0}^{1}{{{x}^{2}}{{e}^{2x}}dx.}\)
-
B.
\(V=\pi \int\limits_{0}^{1}{x{{e}^{x}}dx.}\)
-
C.
\(V=\pi \int\limits_{0}^{1}{{{x}^{2}}{{e}^{2x}}dx.}\)
-
D.
\(V=\pi \int\limits_{0}^{1}{{{x}^{2}}{{e}^{x}}dx.}\)
Đáp án : C
Thể tích khối tròn xoay có được khi quay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),\ \ y=g\left( x \right),\ x=a,\ x=b\) quanh trục \(Ox\) được tính bởi công thức:
\(V=\pi \int\limits_{a}^{b}{\left| {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right|dx.}\)
Áp dụng công thức ta có thể tích khối tròn xoay bài cho là: \(V=\pi \int\limits_{0}^{1}{{{\left( x{{e}^{x}} \right)}^{2}}dx=}\pi \int\limits_{0}^{1}{{{x}^{2}}{{e}^{2x}}dx.}\)
Biết \(\int\limits_{0}^{1}{\frac{\pi {{x}^{3}}+{{2}^{x}}+\text{e}{{x}^{3}}{{.2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{m}+\frac{1}{\text{e}\ln n}\ln \left( p+\frac{\text{e}}{\text{e}+\pi } \right)\) với \(m\), \(n\), \(p\) là các số nguyên dương. Tính tổng \(S=m+n+p\).
-
A.
\(S=6\).
-
B.
\(S=5\).
-
C.
\(S=7\).
-
D.
\(S=8\).
Đáp án : C
Phân tích nhân tử, tách về các tích phân cơ bản
Ta có \(\int\limits_{0}^{1}{\frac{\pi {{x}^{3}}+{{2}^{x}}+\text{e}{{x}^{3}}{{.2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\int\limits_{0}^{1}{\left( {{x}^{3}}+\frac{{{2}^{x}}}{\pi +\text{e}{{.2}^{x}}} \right)\text{d}x}\) \(=\left. \frac{{{x}^{4}}}{4} \right|_{0}^{1}+\int\limits_{0}^{1}{\frac{{{2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{4}+\int\limits_{0}^{1}{\frac{{{2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{4}+J.\)
Tính \(J=\int\limits_{0}^{1}{\frac{{{2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}\).
Đặt \(\pi +\text{e}{{.2}^{x}}=t\Rightarrow \text{e}{{.2}^{x}}\ln 2\text{d}x=\text{d}t\Leftrightarrow {{2}^{x}}\text{d}x=\frac{1}{\text{e}.\ln 2}\text{d}t\).
Đổi cận: Khi \(x=0\) thì \(t=\pi +\text{e}\); khi \(x=1\) thì \(t=\pi +2\text{e}\).
Khi đó \(J=\int\limits_{0}^{1}{\frac{{{2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{\text{e}\ln 2}\int\limits_{\pi +\text{e}}^{\pi +2\text{e}}{\frac{1}{t}\text{d}t}=\frac{1}{\text{e}\ln 2}\left. \ln \left| t \right| \right|_{\pi +\text{e}}^{\pi +2\text{e}}=\frac{1}{\text{e}\ln 2}\ln \left( 1+\frac{\text{e}}{\text{e}+\pi } \right)\).
Suy ra \(\int\limits_{0}^{1}{\frac{\pi {{x}^{3}}+{{2}^{x}}+\text{e}{{x}^{3}}{{.2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{4}+\frac{1}{\text{e}\ln 2}\ln \left( 1+\frac{\text{e}}{\text{e}+\pi } \right)\)\(\Rightarrow m=4\), \(n=2\), \(p=1\).
Vậy \(S=7\).
Tìm thể tích \(V\) của vật tròn xoay sinh ra bởi đường tròn \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\) khi quay quanh trục \(Ox.\)
-
A.
\(V=24{{\pi }^{2}}.\)
-
B.
\(V=24\pi .\)
-
C.
\(V=16\pi .\)
-
D.
\(V=36{{\pi }^{2}}.\)
Đáp án : A
Sử dụng công thức tính thể tích khối tròn xoay được quay quanh trục hoành của các đồ thị hàm số : \(y=f\left( x \right);\ x=a;\ x=b\ \ \left( a<b \right)\) là : \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)}dx.\)
Ta có \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\Leftrightarrow {{\left( y-3 \right)}^{2}}=4-{{x}^{2}}\Leftrightarrow \left[\begin{align} & y=f\left( x \right)=\sqrt{4-{{x}^{2}}}+3 \\ & y=g\left( x \right)=-\,\sqrt{4-{{x}^{2}}}+3 \\\end{align} \right.\)
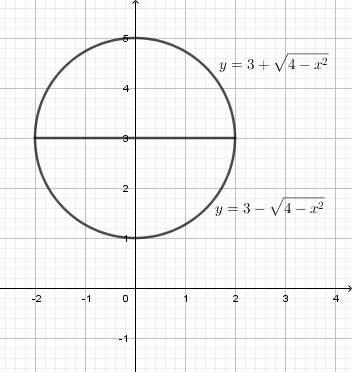
Vậy thể tích khối tròn xoay cần tính là \(V=\pi \int\limits_{-\,2}^{2}{{{f}^{2}}\left( x \right)\,\text{d}x}-\pi \int\limits_{-\,2}^{2}{{{g}^{2}}\left( x \right)\,\text{d}x}\)
\(\begin{align} & =\pi \int\limits_{-\,2}^{2}{\left( {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right)\,\text{d}x} \\ & =\pi \int\limits_{-\,2}^{2}{\left( {{\left( \sqrt{4-{{x}^{2}}}+3 \right)}^{2}}-{{\left( 3-\sqrt{4-{{x}^{2}}} \right)}^{2}} \right)\,\text{d}x} \\ & =\pi \,\int\limits_{-\,2}^{2}{12\sqrt{4-{{x}^{2}}}\,\text{d}x}=24{{\pi }^{2}}. \\\end{align}\)
Vậy thể tích cần tính là \(V=24{{\pi }^{2}}.\)
Cho tích phân $I = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}{\rm{d}}x} = \dfrac{{m - \pi }}{{m + \pi }}$, giá trị của $m$ bằng :
-
A.
$2$.
-
B.
$7$.
-
C.
$4$.
-
D.
$5$.
Đáp án : C
- Sử dụng công thức của tích phân từng phần: \(\int\limits_a^b {udv} = \left. {uv} \right|_a^b - \int\limits_a^b {vdu} \).
- Làm xuất hiện dạng vi phân \(f'\left( x \right)dx\)sau đó đặt \(dv = f'\left( x \right)dx\).
- Đồng nhất thức.
Ta có : \(\left( {x\sin x + \cos x} \right)' = \sin x + x\cos x - \sin x = x\cos x\)
$ \Rightarrow I = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}{\rm{d}}x} = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{\dfrac{x}{{\cos x}}.x\cos x}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dv} $
Đặt $\left\{ \begin{array}{l}u = \dfrac{x}{{\cos x}}\\{\rm{d}}v = \dfrac{{x\cos x}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}{\rm{d}}x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\rm{d}}u = \dfrac{{x\sin x + \cos x}}{{{{\cos }^2}x}}{\rm{d}}x\\v = - \dfrac{1}{{x\sin x + \cos x}}\end{array} \right..$
Khi đó
$\begin{array}{l}I = \left. { - \dfrac{x}{{\cos x}}.\dfrac{1}{{x\sin x + \cos x}}} \right|_0^{\dfrac{\pi }{4}} + \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{{\rm{d}}x}}{{{{\cos }^2}x}}} = \\ = \dfrac{{ - \dfrac{\pi }{4}}}{{\dfrac{{\sqrt 2 }}{2}}}.\dfrac{1}{{\dfrac{\pi }{4}\dfrac{{\sqrt 2 }}{2} + \dfrac{{\sqrt 2 }}{2}}} + \left. {\tan x} \right|_0^{\dfrac{\pi }{4}}\\ = \dfrac{{ - \dfrac{\pi }{4}}}{{\dfrac{1}{2}\left( {\dfrac{\pi }{4} + 1} \right)}} + 1 = \dfrac{{ - 2\pi }}{{\left( {\pi + 4} \right)}} + 1 = \dfrac{{4 - \pi }}{{4 + \pi }} \Rightarrow m = 4\end{array}$.
>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.
 |
 |
 |
 |
 |
 |
 |
 |
