Đề kiểm tra 1 tiết Toán 12 chương 2: Hàm số lũy thừa, mũ và logarit - Đề số 2
Đề bài
Tính tổng \(T\) tất cả các nghiệm của phương trình \({\left( {x - 3} \right)^{2{x^2} - 5x}} = 1\).
-
A.
\(T = \dfrac{{17}}{2}.\)
-
B.
\(T = 4.\)
-
C.
\(T = \dfrac{{13}}{2}.\)
-
D.
\(T = \dfrac{{15}}{2}.\)
Mệnh đề nào đúng với mọi số thực dương $x,y$?
-
A.
${2^{\sqrt x }} = {x^{\sqrt 2 }}$
-
B.
${3^{\sqrt {xy} }} = {\left( {{3^{\sqrt x }}} \right)^{\sqrt y }}$
-
C.
$\dfrac{{{3^{\sqrt[3]{x}}}}}{{{3^{\sqrt[3]{y}}}}} = {3^{\sqrt[3]{{x - y}}}}$
-
D.
${x^{\sqrt 3 }} = {y^{\sqrt 3 }}$
Cho các số \(a,\ b,\ c\) và \(a,\ c\ne 1\). Khẳng định nào sau đây đúng?
-
A.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{b}}c\)
-
B.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{a}}\left( \frac{b}{c} \right)\)
-
C.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{c}}b\)
-
D.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{a}}\left( b-c \right)\)
Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định?
-
A.
\(y = {x^{ - 4}}\).
-
B.
\(y = {x^4}\).
-
C.
$y = {x^{ - \dfrac{3}{4}}}$.
-
D.
$y = \sqrt[3]{x}$.
Giá trị của $x$ thỏa mãn \({\log _{\frac{1}{2}}}(3 - x) = 2\) là
-
A.
$x=3+\sqrt{2}$
-
B.
$x=\dfrac{-11}{4}$
-
C.
$x=3-\sqrt{2}$
-
D.
$x=\dfrac{11}{4}$
Cho hệ phương trình \(\left\{ \begin{array}{l}{\left( {\dfrac{2}{3}} \right)^{2x - y}} + 6{\left( {\dfrac{2}{3}} \right)^{\dfrac{{2x - y}}{2}}} - 7 = 0\\{3^{{{\log }_9}\left( {x - y} \right)}} = 1\end{array} \right.\). Chọn khẳng định đúng?
-
A.
Điều kiện xác định của hệ phương trình là \(x > y > 0\).
-
B.
Điều kiện xác định của hệ phương trình là \(x > y\).
-
C.
Điều kiện xác định của hệ phương trình là \(x \ge y\).
-
D.
Phương trình luôn xác định với mọi \(x,y\).
Tập xác định của hàm số \(f\left( x \right) = \sqrt {{{\log }_{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}}} \) là:
-
A.
\(D = \left( { - \infty ;\dfrac{{ - 3 - \sqrt {17} }}{2}} \right] \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2}; + \infty } \right)\)
-
B.
\(D = \left( { - \infty ; - 3} \right) \cup \left( {1; + \infty } \right)\)
-
C.
\(D = \left( {\dfrac{{ - 3 - \sqrt {17} }}{2}; - 3} \right) \cup \left( {\dfrac{{ - 3 + \sqrt {17} }}{2};1} \right)\)
-
D.
\(D = \left[ {\dfrac{{ - 3 - \sqrt {17} }}{2}; - 3} \right) \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2};1} \right)\)
Tính giá trị \({\left( {\dfrac{1}{{16}}} \right)^{ - 0,75}} + {\left( {\dfrac{1}{8}} \right)^{ - \frac{4}{3}}},\)ta được kết quả là:
-
A.
24
-
B.
12
-
C.
16
-
D.
18
Công thức nào sau đây là công thức tăng trưởng mũ?
-
A.
\(T = A.{e^{Nr}}\)
-
B.
\(T = N.{e^{Ar}}\)
-
C.
\(T = r.{e^{NA}}\)
-
D.
\(T = A.{e^{N - r}}\)
Cho số nguyên dương \(n \ge 2\) và các số thực \(a,b\), nếu có \({a^n} = b\) thì:
-
A.
\(a\) là căn bậc \(b\) của \(n\)
-
B.
\(b\) là căn bậc \(a\) của \(n\)
-
C.
\(a\) là căn bậc \(n\) của \(b\)
-
D.
\(b\) là căn bậc \(n\) của \(a\)
Mệnh đề nào sau đây là mệnh đề đúng ?
-
A.
\({{\left( 2-\sqrt{2} \right)}^{3}}<{{\left( 2-\sqrt{2} \right)}^{4}}\)
-
B.
\({{\left( 4-\sqrt{2} \right)}^{3}}<{{\left( 4-\sqrt{2} \right)}^{4}}\)
-
C.
\({{\left( \sqrt{11}-\sqrt{2} \right)}^{6}}>{{\left( \sqrt{11}-\sqrt{2} \right)}^{7}}\)
-
D.
\({{\left( \sqrt{3}-\sqrt{2} \right)}^{4}}<{{\left( \sqrt{3}-\sqrt{2} \right)}^{5}}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Tập xác định của hàm số \(y = {8^x}\) là
-
A.
\(\mathbb{R}\backslash \left\{ 0 \right\}\)
-
B.
\(\mathbb{R}\)
-
C.
\(\left[ {0; + \infty } \right)\)
-
D.
\(\left( {0; + \infty } \right)\)
Tìm tập nghiệm $S$ của bất phương trình ${2^{x - 1}} > {\left( {\dfrac{1}{{16}}} \right)^{\frac{1}{x}}}$ .
-
A.
\((0, + \infty )\)
-
B.
\(( - \infty , + \infty )\)
-
C.
\((2, + \infty )\)
-
D.
\(( - \infty ,0)\)
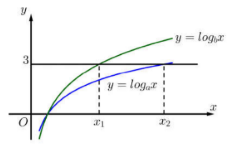
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:
-
A.
\(\dfrac{1}{2}\)
-
B.
\(\sqrt 3 \)
-
C.
\(2\)
-
D.
\(\sqrt[3]{2}\)
Với \(a,\,b\) là các số thực dương bất kì, \({\log _2}\dfrac{a}{{{b^2}}}\) bằng:
-
A.
\(2{\log _2}\dfrac{a}{b}\)
-
B.
\(\dfrac{1}{2}{\log _2}\dfrac{a}{b}\)
-
C.
\({\log _2}a - 2{\log _2}b\)
-
D.
\({\log _2}a - {\log _2}\left( {2b} \right)\)
Cho hàm số \(f\left( x \right) = {\left( {{x^{1 + \dfrac{1}{{2{{\log }_4}x}}}} + {8^{\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} + 1} \right)^{\dfrac{1}{2}}} - 1\) với \(0 < x \ne 1\). Tính giá trị biểu thức \(P = f\left( {f\left( {2018} \right)} \right)\).
-
A.
\(P = 2016\)
-
B.
\(P = 1009\)
-
C.
\(P = 2018\)
-
D.
\(P = {2018^2}\)
Một người mua xe máy với giá 45 triệu đồng. Biết rằng giá trị khấu hao tài sản xe giảm 60% mỗi năm. Hỏi sau bao nhiêu năm thì giá trị xe chỉ còn 5 triệu đồng?
-
A.
\(2\) năm.
-
B.
\(2,5\) năm.
-
C.
\(3\) năm.
-
D.
\(3,5\) năm.
Gọi \(m,M\) lần lượt là GTNN, GTLN của hàm số \(y = {e^{2 - 3x}}\) trên đoạn \(\left[ {0;2} \right]\). Mệnh đề nào sau đây đúng?
-
A.
\(m + M = 1\)
-
B.
\(M - m = e\)
-
C.
\(M.m = \dfrac{1}{{{e^2}}}\)
-
D.
\(\dfrac{M}{m} = {e^2}\)
Tìm số các giá trị nguyên không dương của tham số \(m\) để hàm số \(y = \dfrac{{m\ln x - 2}}{{\ln x + m - 3}}\) đồng biến trên \(\left( {{e^2}; + \infty } \right)\) là
-
A.
\(2\)
-
B.
vô số
-
C.
\(0\)
-
D.
\(1\)
Tính tổng \(T\) tất cả các nghiệm của phương trình \({4.9^x} - {13.6^x} + {9.4^x} = 0\).
-
A.
\(T = 2\).
-
B.
\(T = 3\).
-
C.
\(T = \dfrac{{13}}{4}\).
-
D.
\(T = \dfrac{1}{4}\).
Xét hệ phương trình \(\left\{ \begin{array}{l}{2^x} - {2^y} = y - x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} + xy + {y^2} = 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)có nghiệm \(\left( {x;y} \right)\). Khi đó phát biểu nào sau đây đúng:
-
A.
\({x^2} + {y^2} = 2\)
-
B.
\(x - y = 2\)
-
C.
\(x + y = 2\)
-
D.
\(xy = 2\)
Tìm tập nghiệm $S$ của bất phương trình ${\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}(x) > {\log _2}({x^2} - x) - 1$
-
A.
$S = \left( {2; + \infty } \right)$
-
B.
$S=(1;2)$
-
C.
$S=(0;2)$
-
D.
$S = \left( {1;2} \right]$
Thầy C gửi \(5\) triệu đồng vào ngân hàng với lãi suất \(0,7\% \)/tháng. Chưa đầy một năm thì lãi suất tăng lên thành \(1,15\% \)/tháng. Tiếp theo, sáu tháng sau lãi suất chỉ còn \(0,9\% \)/tháng. Thầy C tiếp tục gửi thêm một số tháng nữa rồi rút cả vỗn lẫn lãi được 5787710,707 đồng. Hỏi thầy C đã gửi tổng thời gian bao nhiêu tháng?
-
A.
\(18\) tháng.
-
B.
\(17\) tháng.
-
C.
\(16\) tháng.
-
D.
\(15\) tháng.
Cho \(x;y\) là hai số thực dương thỏa mãn \(x \ne y\) và \({\left( {{2^x} + \dfrac{1}{{{2^x}}}} \right)^y} < {\left( {{2^y} + \dfrac{1}{{{2^y}}}} \right)^x}.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\).
-
A.
\(\min P = \dfrac{{13}}{2}.\)
-
B.
\(\min P = \dfrac{9}{2}.\)
-
C.
\(\min P = - 2.\)
-
D.
\(\min P = 6.\)
Tìm tất cả các giá trị thực của tham số m để phương trình \({\log _2}\left( {{5^x} - 1} \right).{\log _4}\left( {{{2.5}^x} - 2} \right) = m\) có nghiệm \(x \ge 1\) ?
-
A.
\(m \in \left[ {2; + \infty } \right)\)
-
B.
\(m \in \left[ {3; + \infty } \right)\)
-
C.
\(m \in \left( { - \infty ;2} \right]\)
-
D.
\(m \in \left( { - \infty ;3} \right]\)
Lời giải và đáp án
Tính tổng \(T\) tất cả các nghiệm của phương trình \({\left( {x - 3} \right)^{2{x^2} - 5x}} = 1\).
-
A.
\(T = \dfrac{{17}}{2}.\)
-
B.
\(T = 4.\)
-
C.
\(T = \dfrac{{13}}{2}.\)
-
D.
\(T = \dfrac{{15}}{2}.\)
Đáp án : A
Xét lần lượt các trường hợp cơ số bằng \(1\) và cơ số khác \(1\), tìm nghiệm trong từng trường hợp và kết luận.
Ta xét các trường hợp sau:
TH1. \(x - 3 = 1 \Leftrightarrow x = 4\) thỏa mãn phương trình.
TH2: \(x-3=-1\Leftrightarrow x = 2\) thỏa mãn phương trình.
TH3. \(\left\{ \begin{array}{l}x - 3 \ne 0\\2{x^2} - 5x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{5}{2}\end{array} \right.\).
Vậy phương trình đã cho có ba nghiệm \(x = 0;x=2;{\rm{ }}x = \dfrac{5}{2};{\rm{ }}x = 4\) \( \Rightarrow T = \dfrac{{17}}{2}\)
Mệnh đề nào đúng với mọi số thực dương $x,y$?
-
A.
${2^{\sqrt x }} = {x^{\sqrt 2 }}$
-
B.
${3^{\sqrt {xy} }} = {\left( {{3^{\sqrt x }}} \right)^{\sqrt y }}$
-
C.
$\dfrac{{{3^{\sqrt[3]{x}}}}}{{{3^{\sqrt[3]{y}}}}} = {3^{\sqrt[3]{{x - y}}}}$
-
D.
${x^{\sqrt 3 }} = {y^{\sqrt 3 }}$
Đáp án : B
${2^{\sqrt x }} \ne {x^{\sqrt 2 }}$ nên A sai.
${3^{\sqrt {xy} }} = {3^{\sqrt x .\sqrt y }} = {\left( {{3^{\sqrt x }}} \right)^{\sqrt y }}$ nên B đúng.
$\dfrac{{{3^{\sqrt[3]{x}}}}}{{{3^{\sqrt[3]{y}}}}} = {3^{\sqrt[3]{x} - \sqrt[3]{y}}} \ne {3^{\sqrt[3]{{x - y}}}}$ nên C sai.
${x^{\sqrt 3 }} \ne {y^{\sqrt 3 }}$ nếu $x \ne y$ nên D sai.
Cho các số \(a,\ b,\ c\) và \(a,\ c\ne 1\). Khẳng định nào sau đây đúng?
-
A.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{b}}c\)
-
B.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{a}}\left( \frac{b}{c} \right)\)
-
C.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{c}}b\)
-
D.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{a}}\left( b-c \right)\)
Đáp án : C
Áp dụng các công thức cơ bản của hàm số logarit: \({{\log }_{a}}c={{\log }_{a}}b.{{\log }_{b}}c.\)
Ta có: \(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}=\frac{{{\log }_{a}}c.{{\log }_{c}}b}{{{\log }_{a}}c}={{\log }_{c}}b.\)
Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định?
-
A.
\(y = {x^{ - 4}}\).
-
B.
\(y = {x^4}\).
-
C.
$y = {x^{ - \dfrac{3}{4}}}$.
-
D.
$y = \sqrt[3]{x}$.
Đáp án : D
Tính đạo hàm của mỗi hàm số rồi xét dấu đạo hàm trên khoảng xác định \(D\).
Nếu \(y' \ge 0\) và bằng \(0\) tại hữu hạn điểm thuộc \(D\) thì hàm số đồng biến trên \(D\).
Hàm số \(y = {x^{ - 4}}\) có tập xác định là \(\mathbb{R}\backslash \left\{ 0 \right\}\) và có \(y' = - 4{x^{ - 5}}\) nên không đồng biến trên các khoảng xác định (đồng biến trên \(\left( { - \infty ,0} \right)\) và nghịch biến trên \(\left( {0, + \infty } \right)\)), loại A.
Hàm số \(y = {x^{ - \dfrac{3}{4}}}\) có tập xác định là \(\left( {0, + \infty } \right)\) và có \(y' = - \dfrac{3}{4}{x^{ - \dfrac{7}{4}}} < 0,\forall x \in \left( {0, + \infty } \right)\) nên không đồng biến trên từng khoảng xác định, loại B.
Hàm số \(y = {x^4}\) có tập xác định là \(\mathbb{R}\) và có \(y' = 4{x^3}\) nên không đồng biến trên các khoảng xác định, loại C.
Hàm số \(y = \sqrt[3]{x}\) có tập xác định là \(\mathbb{R}\) và có \(y' = \dfrac{1}{{3\sqrt[3]{{{x^2}}}}} > 0\) nên hàm số đồng biến trên các khoảng xác định.
Giá trị của $x$ thỏa mãn \({\log _{\frac{1}{2}}}(3 - x) = 2\) là
-
A.
$x=3+\sqrt{2}$
-
B.
$x=\dfrac{-11}{4}$
-
C.
$x=3-\sqrt{2}$
-
D.
$x=\dfrac{11}{4}$
Đáp án : D
Sử dụng phương pháp giải phương trình logarit cơ bản \({\log _a}x = m\left( {0 < a \ne 1} \right) \Leftrightarrow x = {a^m}\)
Phương trình tương đương với:
\(3 - x = {\left( {\dfrac{1}{2}} \right)^2} \Leftrightarrow x = \dfrac{{11}}{4}\)
Vậy $x = \dfrac{{11}}{4}$.
Cho hệ phương trình \(\left\{ \begin{array}{l}{\left( {\dfrac{2}{3}} \right)^{2x - y}} + 6{\left( {\dfrac{2}{3}} \right)^{\dfrac{{2x - y}}{2}}} - 7 = 0\\{3^{{{\log }_9}\left( {x - y} \right)}} = 1\end{array} \right.\). Chọn khẳng định đúng?
-
A.
Điều kiện xác định của hệ phương trình là \(x > y > 0\).
-
B.
Điều kiện xác định của hệ phương trình là \(x > y\).
-
C.
Điều kiện xác định của hệ phương trình là \(x \ge y\).
-
D.
Phương trình luôn xác định với mọi \(x,y\).
Đáp án : B
Biểu thức \(y = {\log _a}f\left( x \right)\) xác định nếu \(f\left( x \right)\) xác định và \(f\left( x \right) > 0\).
Điều kiện: \(x - y > 0 \Leftrightarrow x > y\). Do đó B đúng và các đáp án còn lại sai.
Tập xác định của hàm số \(f\left( x \right) = \sqrt {{{\log }_{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}}} \) là:
-
A.
\(D = \left( { - \infty ;\dfrac{{ - 3 - \sqrt {17} }}{2}} \right] \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2}; + \infty } \right)\)
-
B.
\(D = \left( { - \infty ; - 3} \right) \cup \left( {1; + \infty } \right)\)
-
C.
\(D = \left( {\dfrac{{ - 3 - \sqrt {17} }}{2}; - 3} \right) \cup \left( {\dfrac{{ - 3 + \sqrt {17} }}{2};1} \right)\)
-
D.
\(D = \left[ {\dfrac{{ - 3 - \sqrt {17} }}{2}; - 3} \right) \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2};1} \right)\)
Đáp án : D
Hàm số \(y = {\log _a}x\) xác định \( \Leftrightarrow \left\{ \begin{array}{l}x > 0\\0 < a \ne 1\end{array} \right.\)
Hàm số \(y = \sqrt A \) xác định \( \Leftrightarrow A \ge 0\)
Hàm số có dạng \(\dfrac{A}{B}\) xác định khi và chỉ khi \(B \ne 0\).
Hàm số \(f\left( x \right) = \sqrt {{{\log }_{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}}} \) xác định
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\log _{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}} \ge 0\\\dfrac{{3 - 2x - {x^2}}}{{x + 1}} > 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\log _{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}} \ge {\log _{\dfrac{1}{2}}}1\\\dfrac{{ - \left( {x - 1} \right)\left( {x + 3} \right)}}{{x + 1}} > 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{3 - 2x - {x^2}}}{{x + 1}} \le 1\\\left[ \begin{array}{l}x < - 3\\ - 1 < x < 1\end{array} \right.\\x \ne - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{3 - 2x - {x^2} - x - 1}}{{x + 1}} \le 0\\\left[ \begin{array}{l}x < - 3\\ - 1 < x < 1\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{ - {x^2} - 3x + 2}}{{x + 1}} \le 0\\\left[ \begin{array}{l}x < - 3\\ - 1 < x < 1\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}\dfrac{{ - 3 - \sqrt {17} }}{2} \le x \le - 1\\x \ge \dfrac{{ - 3 + \sqrt {17} }}{2}\end{array} \right.\\\left[ \begin{array}{l}x < - 3\\ - 1 < x < 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\dfrac{{ - 3 - \sqrt {17} }}{2} \le x < - 3\\\dfrac{{ - 3 + \sqrt {17} }}{2} \le x < 1\end{array} \right.\end{array}\)
Vậy tập xác định của phương trình là \(D = \left[ {\dfrac{{ - 3 - \sqrt {17} }}{2}; - 3} \right) \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2};1} \right)\)
Tính giá trị \({\left( {\dfrac{1}{{16}}} \right)^{ - 0,75}} + {\left( {\dfrac{1}{8}} \right)^{ - \frac{4}{3}}},\)ta được kết quả là:
-
A.
24
-
B.
12
-
C.
16
-
D.
18
Đáp án : A
Sử dụng công thức \(\dfrac{1}{{{x^m}}} = {x^{ - m}},\,\,{\left( {{x^m}} \right)^n} = {x^{mn}}\).
\({\left( {\dfrac{1}{{16}}} \right)^{ - 0,75}} + {\left( {\dfrac{1}{8}} \right)^{ - \frac{4}{3}}} = {16^{0,75}} + {8^{\frac{4}{3}}} = {\left( {{2^4}} \right)^{\frac{3}{4}}} + {\left( {{2^3}} \right)^{\frac{4}{3}}} = {2^3} + {2^4} = 24\).
Công thức nào sau đây là công thức tăng trưởng mũ?
-
A.
\(T = A.{e^{Nr}}\)
-
B.
\(T = N.{e^{Ar}}\)
-
C.
\(T = r.{e^{NA}}\)
-
D.
\(T = A.{e^{N - r}}\)
Đáp án : A
Công thức lãi kép (hoặc công thức tăng trưởng mũ):
\(T = A.{e^{Nr}}\), ở đó \(A\) là số tiền gửi ban đầu, \(r\) là lãi suất, \(N\) là số kì hạn.
Cho số nguyên dương \(n \ge 2\) và các số thực \(a,b\), nếu có \({a^n} = b\) thì:
-
A.
\(a\) là căn bậc \(b\) của \(n\)
-
B.
\(b\) là căn bậc \(a\) của \(n\)
-
C.
\(a\) là căn bậc \(n\) của \(b\)
-
D.
\(b\) là căn bậc \(n\) của \(a\)
Đáp án : C
Cho số thực \(b\) và số nguyên dương \(n\left( {n \ge 2} \right)\). Số \(a\) được gọi là căn bậc \(n\) của số \(b\) nếu \({a^n} = b\).
Cho số thực \(b\) và số nguyên dương \(n\left( {n \ge 2} \right)\). Nếu có \({a^n} = b\) thì \(a\) được gọi là căn bậc \(n\) của \(b\).
Mệnh đề nào sau đây là mệnh đề đúng ?
-
A.
\({{\left( 2-\sqrt{2} \right)}^{3}}<{{\left( 2-\sqrt{2} \right)}^{4}}\)
-
B.
\({{\left( 4-\sqrt{2} \right)}^{3}}<{{\left( 4-\sqrt{2} \right)}^{4}}\)
-
C.
\({{\left( \sqrt{11}-\sqrt{2} \right)}^{6}}>{{\left( \sqrt{11}-\sqrt{2} \right)}^{7}}\)
-
D.
\({{\left( \sqrt{3}-\sqrt{2} \right)}^{4}}<{{\left( \sqrt{3}-\sqrt{2} \right)}^{5}}\)
Đáp án : B
\({a^x} < {a^y} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a > 1\\x < y\end{array} \right.\\\left\{ \begin{array}{l}0 < a < 1\\x > y\end{array} \right.\end{array} \right.\)
\(0<2-\sqrt{2}<1\Rightarrow {{\left( 2-\sqrt{2} \right)}^{3}}>{{\left( 2-\sqrt{2} \right)}^{4}}\Rightarrow \)Đáp án A sai.
\(4-\sqrt{2}>1\Rightarrow {{\left( 4-\sqrt{2} \right)}^{3}}<{{\left( 4-\sqrt{2} \right)}^{4}}\Rightarrow \)Đáp án B đúng.
\(\sqrt{11}-\sqrt{2}>1\Rightarrow {{\left( \sqrt{11}-\sqrt{2} \right)}^{6}}<{{\left( \sqrt{11}-\sqrt{2} \right)}^{7}}\Rightarrow \) Đáp án C sai.
\(0<\sqrt{3}-\sqrt{2}<1\Rightarrow {{\left( \sqrt{3}-\sqrt{2} \right)}^{4}}>{{\left( \sqrt{3}-\sqrt{2} \right)}^{5}}\Rightarrow \)Đáp án D sai.
Đề thi THPT QG – 2021 lần 1– mã 104
Tập xác định của hàm số \(y = {8^x}\) là
-
A.
\(\mathbb{R}\backslash \left\{ 0 \right\}\)
-
B.
\(\mathbb{R}\)
-
C.
\(\left[ {0; + \infty } \right)\)
-
D.
\(\left( {0; + \infty } \right)\)
Đáp án : B
Tập xác định của hàm số mũ \(y = {a^x}\) là \(\mathbb{R}\)
Tập xác định của hàm số \(y = {8^x}\) là \(\mathbb{R}\)
Tìm tập nghiệm $S$ của bất phương trình ${2^{x - 1}} > {\left( {\dfrac{1}{{16}}} \right)^{\frac{1}{x}}}$ .
-
A.
\((0, + \infty )\)
-
B.
\(( - \infty , + \infty )\)
-
C.
\((2, + \infty )\)
-
D.
\(( - \infty ,0)\)
Đáp án : A
Biến đổi đưa bất phương trình đã cho về dạng cơ bản \({2^x} > {2^y}\) . Sử dụng tính đồng biến, nghịch biến của hàm số mũ:
Khi \(a > 1\) thì \({a^x} > {a^y} \Leftrightarrow x > y\)
Khi \(0 < a < 1\) thì \({a^x} > {a^y} \Leftrightarrow x < y\)
Ta có
\({2^{x - 1}} > {\left( {\dfrac{1}{{16}}} \right)^{\frac{1}{x}}} \Leftrightarrow {2^{x - 1}} > {\left( {{2^{ - 4}}} \right)^{\frac{1}{x}}} \Leftrightarrow {2^{x - 1}} > {2^{ - \frac{4}{x}}} \)
$\Leftrightarrow x - 1 > - \dfrac{4}{x} \Leftrightarrow x + \dfrac{4}{x} - 1 > 0 \Leftrightarrow \dfrac{{{x^2} - x + 4}}{x} > 0$
Vì ${x^2} - x + 4 > 0$ nên suy ra $x > 0$
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:

-
A.
\(\dfrac{1}{2}\)
-
B.
\(\sqrt 3 \)
-
C.
\(2\)
-
D.
\(\sqrt[3]{2}\)
Đáp án : D
Dựa vào đồ thị hàm số, xác định các giá trị của \({x_1},\,{x_2}\) theo \(a\) và \(b.\) Từ đó tính giá trị của \(\dfrac{a}{b}.\)
Dựa vào đồ thị hàm số ta thấy \({x_1}\) là nghiệm của phương trình hoành độ giao điểm \({\log _b}{x_1} = 3 \Leftrightarrow {x_1} = {b^3}.\)
Và \({x_2}\) là nghiệm của phương trình hoành độ giao điểm \({\log _a}{x_2} = 3 \Leftrightarrow {x_2} = {a^3}.\)
Theo đề bài ta có: \({x_2} = 2{x_1} \Rightarrow {a^3} = 2{b^3} \Leftrightarrow \dfrac{{{a^3}}}{{{b^3}}} = 2 \Leftrightarrow \dfrac{a}{b} = \sqrt[3]{2}.\)
Với \(a,\,b\) là các số thực dương bất kì, \({\log _2}\dfrac{a}{{{b^2}}}\) bằng:
-
A.
\(2{\log _2}\dfrac{a}{b}\)
-
B.
\(\dfrac{1}{2}{\log _2}\dfrac{a}{b}\)
-
C.
\({\log _2}a - 2{\log _2}b\)
-
D.
\({\log _2}a - {\log _2}\left( {2b} \right)\)
Đáp án : C
Sử dụng các công thức: \(lo{g_a}\dfrac{b}{c} = lo{g_a}b - lo{g_a}c;\,\,\,{\log _{{a^m}}}b = \dfrac{1}{m}{\log _a}b;\,\,\,{\log _a}{b^n} = n{\log _a}b.\)
Ta có: \({\log _2}\dfrac{a}{{{b^2}}} = {\log _2}a - {\log _2}{b^2} = {\log _2}a - 2{\log _a}b.\)
Cho hàm số \(f\left( x \right) = {\left( {{x^{1 + \dfrac{1}{{2{{\log }_4}x}}}} + {8^{\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} + 1} \right)^{\dfrac{1}{2}}} - 1\) với \(0 < x \ne 1\). Tính giá trị biểu thức \(P = f\left( {f\left( {2018} \right)} \right)\).
-
A.
\(P = 2016\)
-
B.
\(P = 1009\)
-
C.
\(P = 2018\)
-
D.
\(P = {2018^2}\)
Đáp án : C
Sử dụng các công thức biến đổi logarit \({\log _a}{a^n} = n;{\log _a}b = \dfrac{1}{{{{\log }_b}a}};{a^{{{\log }_a}b}} = b\)
Ta có:
\(\begin{array}{l}{x^{1 + \dfrac{1}{{2{{\log }_4}x}}}} = {x^{1 + \dfrac{1}{{{{\log }_2}x}}}} = {x^{1 + {{\log }_x}2}} = {x^{{{\log }_x}2x}} = 2x\\{8^{\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} = {2^{3.\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} = {2^{\dfrac{1}{{{{\log }_{{x^2}}}2}}}} = {2^{{{\log }_2}{x^2}}} = {x^2}\end{array}\)
Khi đó \(f\left( x \right) = {\left( {{x^2} + 2x + 1} \right)^{\dfrac{1}{2}}} - 1 = {\left( {{{\left( {x + 1} \right)}^2}} \right)^{\dfrac{1}{2}}} - 1 = x \Rightarrow f\left( x \right) = x\)
Do đó \(P = f\left( {f\left( {2018} \right)} \right) = f\left( {2018} \right) = 2018\).
Một người mua xe máy với giá 45 triệu đồng. Biết rằng giá trị khấu hao tài sản xe giảm 60% mỗi năm. Hỏi sau bao nhiêu năm thì giá trị xe chỉ còn 5 triệu đồng?
-
A.
\(2\) năm.
-
B.
\(2,5\) năm.
-
C.
\(3\) năm.
-
D.
\(3,5\) năm.
Đáp án : B
Lập công thức tổng quát cho giá trị xe sau \(n\) năm. Từ đó tìm được \(n\).
Gọi số năm để xe có giá trị 5 triệu đồng là \(n\left( {n \in {N^*}} \right)\)
Sau \(n\) năm giá trị xe còn lại là: \({T_n} = {T_0}{\left( {1 - 60\% } \right)^n}\) với \({T_n}\) là giá xe sau \(n\) năm, \({T_o}\) là giá xe ban đầu
Khi đó ta có: \(5 = 45.0,{4^n} \Rightarrow 0,{4^n} = \dfrac{1}{9}\) nên \(n = {\log _{0,4}}\dfrac{1}{9} \approx 2,39\)
Vậy sau 2,5 năm giá trị xe chỉ còn 5 triệu đồng
Gọi \(m,M\) lần lượt là GTNN, GTLN của hàm số \(y = {e^{2 - 3x}}\) trên đoạn \(\left[ {0;2} \right]\). Mệnh đề nào sau đây đúng?
-
A.
\(m + M = 1\)
-
B.
\(M - m = e\)
-
C.
\(M.m = \dfrac{1}{{{e^2}}}\)
-
D.
\(\dfrac{M}{m} = {e^2}\)
Đáp án : C
- Bước 1: Tính \(y'\), tìm các nghiệm \({x_1},{x_2},...,{x_n} \in \left[ {a;b} \right]\) của phương trình \(y' = 0\).
- Bước 2: Tính \(f\left( a \right),f\left( b \right),f\left( {{x_1}} \right),...,f\left( {{x_n}} \right)\).
- Bước 3: So sánh các giá trị vừa tính ở trên và kết luận GTLN, GTNN của hàm số.
+ GTNN \(m\) là số nhỏ nhất trong các giá trị tính được.
+ GTLN \(M\) là số lớn nhất trong các giá trị tính được.
Ta có: \(f'\left( x \right) = - 3{e^{2 - 3x}} < 0,\forall x \in R\).
Do đó hàm số \(f\left( x \right)\) lên tục và nghịch biến trên \(\left[ {0;2} \right]\).
Do đó \(m = \mathop {\min }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 2 \right) = \dfrac{1}{{{e^4}}};M = \mathop {\max }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 0 \right) = {e^2} \Rightarrow M.m = \dfrac{1}{{{e^2}}}\)
Tìm số các giá trị nguyên không dương của tham số \(m\) để hàm số \(y = \dfrac{{m\ln x - 2}}{{\ln x + m - 3}}\) đồng biến trên \(\left( {{e^2}; + \infty } \right)\) là
-
A.
\(2\)
-
B.
vô số
-
C.
\(0\)
-
D.
\(1\)
Đáp án : C
- Đặt ẩn phụ\(t = \ln x\), đưa hàm số về hàm số ẩn \(t\).
- Tìm điều kiện của ẩn phụ.
- Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {a;b} \right)\) khi nó xác định và liên tục trên khoảng \(\left( {a;b} \right)\) đồng thời\(f'\left( x \right) \ge 0,\forall x \in \left( {a;b} \right)\). (Dấu ‘=’ chỉ xảy ra tại một số hữu hạn điểm).
- Tìm các giá trị nguyên không dương của \(m\) thỏa mãn.
Đặt \(t = \ln x,\,\,\,t \in \mathbb{R}.\) Hàm số đã cho trở thành \(y = \dfrac{{mt - 2}}{{t + m - 3}}\,\,\,\left( {t \ne 3 - m} \right)\) (1)
Xét hàm số \(t = \ln x\) với\(x \in \left( {{e^2}; + \infty } \right)\)ta có: \(t'\left( x \right) = \dfrac{1}{x} > 0\,\,\forall x \in \left( {{e^2}; + \infty } \right)\).
Do đó hàm số \(t = \ln x\) đồng biến trên khoảng \(\left( {{e^2}; + \infty } \right)\), do đó ta có: \(t \in \left( {2; + \infty } \right)\).
Yêu cầu bài toán trở thành : Tìm số các giá trị nguyên không dương của tham số \(m\) để hàm số \(y = f\left( t \right) = \dfrac{{mt - 2}}{{t + m - 3}}\) đồng biến trên khoảng \(\left( {2; + \infty } \right)\).
Ta có: \(f'\left( t \right) = \dfrac{{m\left( {m - 3} \right) + 2}}{{{{\left( {t + m - 3} \right)}^2}}} = \dfrac{{{m^2} - 3m + 2}}{{{{\left( {t + m - 3} \right)}^2}}}.\)
Hàm số \(y = f\left( t \right)\) đồng biến trên khoảng \(\left( {2; + \infty } \right)\) khi nó xác định trên khoảng \(\left( {2; + \infty } \right)\) đồng thời \(f'\left( t \right) \ge 0,\,\,\,\forall t \in \left( {2; + \infty } \right)\) (Dấu ‘=’ chỉ xảy ra tại một số hữu hạn điểm).
Do đó, \(\left\{ \begin{array}{l}t \ne 3 - m\,\,\forall t \in \left( {2; + \infty } \right)\\{m^2} - 3m + 2 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3 - m \le 2\\\left[ \begin{array}{l}m > 2\\m < 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ge 1\\\left[ \begin{array}{l}m > 2\\m < 1\end{array} \right.\end{array} \right. \Leftrightarrow m > 2.\)
Suy ra không có giá trị nguyên không dương nào của \(m\) thỏa mãn yêu cầu bài toán.
Tính tổng \(T\) tất cả các nghiệm của phương trình \({4.9^x} - {13.6^x} + {9.4^x} = 0\).
-
A.
\(T = 2\).
-
B.
\(T = 3\).
-
C.
\(T = \dfrac{{13}}{4}\).
-
D.
\(T = \dfrac{1}{4}\).
Đáp án : A
- Chia cả hai vế cho $9^x$.
- Giải phương trình bậc hai ẩn ${\left( {\dfrac{2}{3}} \right)^x}$.
\(\begin{array}{l}{4.9^x} - {13.6^x} + {9.4^x} = 0 \Leftrightarrow 4 - 13.{\left( {\dfrac{2}{3}} \right)^x} + 9.{\left( {\dfrac{2}{3}} \right)^{2x}} = 0 \Leftrightarrow \left[ \begin{array}{l}{\left( {\dfrac{2}{3}} \right)^x} = 1\\{\left( {\dfrac{2}{3}} \right)^x} = \dfrac{4}{9}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right. \Rightarrow T = 0 + 2 = 2\end{array}\)
Xét hệ phương trình \(\left\{ \begin{array}{l}{2^x} - {2^y} = y - x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} + xy + {y^2} = 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)có nghiệm \(\left( {x;y} \right)\). Khi đó phát biểu nào sau đây đúng:
-
A.
\({x^2} + {y^2} = 2\)
-
B.
\(x - y = 2\)
-
C.
\(x + y = 2\)
-
D.
\(xy = 2\)
Đáp án : A
Biến đổi phương trình \(\left( 1 \right)\) về dạng đặc biệt rồi dùng hàm đặc trưng giải phương trình.
Ta có: \(\left( 1 \right) \Leftrightarrow {2^x} + x = {2^y} + y\,\,\,\,\,\,\,\,\left( * \right)\)
Xét hàm số \(f\left( t \right) = {2^t} + t\) trên \(\mathbb{R},\) ta có: \(f'\left( t \right) = {2^t}\ln 2 + 1 > 0,\,\forall t \in \mathbb{R}.\)
Vậy hàm số \(f\left( t \right)\) đồng biến trên \(\mathbb{R}.\)
Do đó: \(\left( * \right) \Leftrightarrow f\left( x \right) = f\left( y \right) \Leftrightarrow x = y.\)
Thay \(x = y\) vào (2) ta được: \(3{x^2} = 3 \Leftrightarrow {x^2} = 1 \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = 1\\x = - 1 \Rightarrow y = - 1\end{array} \right. \Rightarrow \left( {x;y} \right) = \left( {1;1} \right),\left( { - 1; - 1} \right).\)
Tìm tập nghiệm $S$ của bất phương trình ${\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}(x) > {\log _2}({x^2} - x) - 1$
-
A.
$S = \left( {2; + \infty } \right)$
-
B.
$S=(1;2)$
-
C.
$S=(0;2)$
-
D.
$S = \left( {1;2} \right]$
Đáp án : B
Dùng máy tính thử một số giá trị để loại các đáp án
Thử giá trị $x = 3:{\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}\left( x \right) - {\log _2}\left( {{x^2} - x} \right) + 1 < 0$: Loại đáp án A
Thử giá trị $x = 2:{\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}\left( x \right) - {\log _2}\left( {{x^2} - x} \right) + 1 = 0$: Loại đáp án D
Thử giá trị $x = 0,5$: MATH ERROR: Loại đáp án C
Thầy C gửi \(5\) triệu đồng vào ngân hàng với lãi suất \(0,7\% \)/tháng. Chưa đầy một năm thì lãi suất tăng lên thành \(1,15\% \)/tháng. Tiếp theo, sáu tháng sau lãi suất chỉ còn \(0,9\% \)/tháng. Thầy C tiếp tục gửi thêm một số tháng nữa rồi rút cả vỗn lẫn lãi được 5787710,707 đồng. Hỏi thầy C đã gửi tổng thời gian bao nhiêu tháng?
-
A.
\(18\) tháng.
-
B.
\(17\) tháng.
-
C.
\(16\) tháng.
-
D.
\(15\) tháng.
Đáp án : C
Gọi x: số tháng gửi với \(r = 0,7\% /\)tháng
y: số tháng gửi với \(r = 0,9\% /\)tháng
\( + )\) Tổng số tháng gửi tiết kiệm: \(x + 6 + y\) (tháng)
\( + )\) Theo đề bài ta có: \(\left[ {\left[ {5000000{{\left( {1 + 0,7\% } \right)}^x}} \right]{{\left( {1 + 1,15\% } \right)}^6}} \right]{\left( {1 + 0,9\% } \right)^y} = 5787710,707\)
\( \Leftrightarrow {\left( {1,007} \right)^x}.{\left( {1,009} \right)^y} = 1,080790424\)
\( \Leftrightarrow {\left( {1,009} \right)^y} = \dfrac{{1,080790424}}{{{{\left( {1,007} \right)}^x}}}\)
\( \Leftrightarrow y = {\log _{1,009}}\dfrac{{1,080790424}}{{{{\left( {1,007} \right)}^x}}} = f\left( x \right)\)
Nhập \(f\left( x \right)\) vào TABLE \(\left\{ \begin{array}{l}F\left( x \right) = {\log _{1,009}}\dfrac{{1,080790424}}{{{{\left( {1,007} \right)}^x}}}\\Start:1\\End:11\\Step:1\end{array} \right.\)
Khi đó bảng giá trị hiện ra x=6 thì y=3,9999.
\( + )\) Vì x, y nguyên \( \Rightarrow \)\(\left\{ \begin{array}{l}x = 6\\y = 4\end{array} \right.\)
\( \Rightarrow \) Số tháng gửi tiết kiệm là:
\( 6 + 6 + 4 = 16\) (tháng)
Cho \(x;y\) là hai số thực dương thỏa mãn \(x \ne y\) và \({\left( {{2^x} + \dfrac{1}{{{2^x}}}} \right)^y} < {\left( {{2^y} + \dfrac{1}{{{2^y}}}} \right)^x}.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\).
-
A.
\(\min P = \dfrac{{13}}{2}.\)
-
B.
\(\min P = \dfrac{9}{2}.\)
-
C.
\(\min P = - 2.\)
-
D.
\(\min P = 6.\)
Đáp án : D
Đưa biểu thức cần tìm giá trị nhỏ nhất về dạng phương trình bậc hai ẩn y.
Ta có
\(\begin{array}{l}P = \dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\\ \Leftrightarrow Pxy - P{y^2} = {x^2} + 3{y^2}\\ \Leftrightarrow \left( {P + 3} \right){y^2} - Pxy + {x^2} = 0\end{array}\)
Phương trình trên có nghiệm khi
\(\begin{array}{l}\Delta = {P^2}{x^2} - 4\left( {P + 3} \right){x^2} \ge 0\\ \Leftrightarrow {P^2} - 4P - 12 \ge 0\\ \Rightarrow \left[ \begin{array}{l}P \ge 6\\P \le - 2\end{array} \right. \Rightarrow MinP = 6\end{array}\)
Dấu bằng xáy ra khi \(\left\{ \begin{array}{l}y = \dfrac{{Px}}{{2\left( {P + 3} \right)}} = \dfrac{x}{3}\\\dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}} = 6\end{array} \right. \Rightarrow x = 3y\)
Dễ thấy \(x=3y\) thỏa mãn điều kiện bài cho vì:
$\begin{array}{l}
{\left( {{2^{3y}} + \frac{1}{{{2^{3y}}}}} \right)^y} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^{3y}}\\
\Leftrightarrow {2^{3y}} + \frac{1}{{{2^{3y}}}} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^3}\\
\Leftrightarrow {2^{3y}} + \frac{1}{{{2^{3y}}}} < {2^{3y}} + \frac{1}{{{2^{3y}}}} + {3.2^y}.\frac{1}{{{2^y}}}.\left( {{2^y} + \frac{1}{{{2^y}}}} \right)\\
\Leftrightarrow 0 < 3\left( {{2^y} + \frac{1}{{{2^y}}}} \right)
\end{array}$
Bđt trên luôn đúng với mọi \(y>0\).
Tìm tất cả các giá trị thực của tham số m để phương trình \({\log _2}\left( {{5^x} - 1} \right).{\log _4}\left( {{{2.5}^x} - 2} \right) = m\) có nghiệm \(x \ge 1\) ?
-
A.
\(m \in \left[ {2; + \infty } \right)\)
-
B.
\(m \in \left[ {3; + \infty } \right)\)
-
C.
\(m \in \left( { - \infty ;2} \right]\)
-
D.
\(m \in \left( { - \infty ;3} \right]\)
Đáp án : B
Đặt \(t = {\log _2}\left( {{5^x} - 1} \right)\) , tìm tập giá trị của t tương ứng với \(x \ge 1\).
Để phương trình về dạng \(f\left( t \right) = m\,\,\left( * \right)\), khi đó số nghiệm của phương trình (*) chính là số giao điểm của đồ thị hàm số y = f(t) và đường thẳng y = m song song với trục hoành.
ĐK: \({5^x} - 1 > 0 \Leftrightarrow {5^x} > 1 \Leftrightarrow x > 0\)
\(\begin{array}{l}{\log _2}\left( {{5^x} - 1} \right).{\log _4}\left( {{{2.5}^x} - 2} \right) = m\\ \Leftrightarrow {\log _2}\left( {{5^x} - 1} \right).{\log _{{2^2}}}\left[ {2\left( {{5^x} - 1} \right)} \right] = m\\ \Leftrightarrow {\log _2}\left( {{5^x} - 1} \right).\dfrac{1}{2}\left[ {{{\log }_2}2 + {{\log }_2}\left( {{5^x} - 1} \right)} \right] = m\\ \Leftrightarrow \log _2^2\left( {{5^x} - 1} \right) + {\log _2}\left( {{5^x} - 1} \right) = 2m\end{array}\)
Đặt \(t = {\log _2}\left( {{5^x} - 1} \right)\), với \(x \ge 1\) ta có \({5^x} \ge 5 \Rightarrow {5^x} - 1 \ge 4 \Rightarrow {\log _2}\left( {{5^x} - 1} \right) \ge {\log _2}4 = 2\)
Khi đó phương trình trở thành \({t^2} + t = 2m\,\,\left( {t \ge 2} \right)\,\,\,\left( * \right)\). Để phương trình ban đầu có nghiệm \(x \ge 1\) khi và chỉ khi phương trình (*) có nghiệm \(t \ge 2\).
Xét hàm số \(f\left( t \right) = {t^2} + t\) trên \(\left[ {2; + \infty } \right)\), ta có \(f'\left( t \right) = 2t + 1 = 0 \Leftrightarrow t = - \dfrac{1}{2}\). Lập BBT

Dựa vào BBT ta thấy phương trình (*) có nghiệm \(t \ge 2\) khi và chỉ khi \(2m \ge 6 \Leftrightarrow m \ge 3 \Rightarrow m \in \left[ {3; + \infty } \right)\)
















