Đề khảo sát chất lượng đầu năm Toán 12 THPT Yên Mô B
Một người cần sơn các mặt của một cái bục (trừ đáy lớn) để đặt một bức tượng. Giá trị còn lại của một chiếc xe theo thời gian khấu hao được xác định bởi công thức: Một hộp có 15 chiếc thẻ được đánh số lần lượt từ 1 đến 15. Chọn ngẫu nhiên 3 thẻ từ hộp đó. Một loại thuốc được dùng mỗi ngày một lần. Lúc đầu nồng độ thuốc trong máu của bệnh nhân tăng nhanh.
Đề bài
Rút gọn biểu thức \( T = \sin( \frac{\pi}{3}+x)-\sin( \frac{\pi}{3})-x \) ta được kết quả là
-
A.
\( T = \frac{\sqrt{3}}{2} \).
-
B.
\( T = \sin 2x \).
-
C.
\( T = \sqrt{3} \cos x \).
-
D.
\( T = \sin x \).
Cho \( (u_n) \) là cấp số cộng có số hạng đầu bằng 2, công sai bằng 5. Tổng 10 số hạng đầu tiên của cấp số cộng đó bằng?
-
A.
-410.
-
B.
-205.
-
C.
245.
-
D.
-230.
Cho hình chóp tứ giác S.ABCD . Gọi M, N lần lượt là trung điểm của SB và BD. Khẳng định nào sau đây đúng?
-
A.
\( MN \parallel (SAD) \).
-
B.
\( MN \parallel (SBC) \).
-
C.
\( MN \parallel (SAB) \).
-
D.
\( MN \parallel (SAC) \).
Hàm số nào sau đây liên tục tại \( x = 1 \)?
-
A.
\( f(x) = \begin{cases} \frac{x^2 - 1}{x - 1} & \text{khi } x < 1 \\ 2x + 1 & \text{khi } x \ge 1 \end{cases} \).
-
B.
\( f(x) = \begin{cases} \frac{x^2 - 1}{x - 1} & \text{khi } x < 1 \\ 2x & \text{khi } x \ge 1 \end{cases} \).
-
C.
\( f(x) = \begin{cases} \frac{x^2 - 1}{x - 1} & \text{khi } x < 1 \\ 2x - 1 & \text{khi } x \ge 1 \end{cases} \).
-
D.
\( f(x) = \begin{cases} \frac{x^2 - 1}{x - 1} & \text{khi } x < 1 \\ x - 1 & \text{khi } x \ge 1 \end{cases} \).
Cho biểu thức \(T = {x^{ - \frac{3}{4}}}\sqrt[4]{{{x^5}}}\) \((x > 0)\). Khẳng định nào sau đây đúng?
-
A.
\( T = x^{-\frac{1}{2}} \).
-
B.
\( T = x^{-2} \).
-
C.
\( T = x^{\frac{1}{2}} \).
-
D.
\( T = x^{2} \).
Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng 2a , cạnh bên bằng a. Tính số đo của góc nhị diện [A, B'C', A']
-
A.
\( 30^\circ \).
-
B.
\( 60^\circ \).
-
C.
\( 45^\circ \).
-
D.
\( 90^\circ \).
Cho hình chóp S.ABC , biết \( SA \perp (ABC) \) và tam giác ABC vuông tại A . Đường thẳng AB vuông góc với mặt phẳng nào sau đây?
-
A.
(SAB).
-
B.
(SAC).
-
C.
(SBC).
-
D.
(ABC).
Hai xạ thủ A và B cùng bắn súng một cách độc lập. Xác suất bắn trúng bia của hai xạ thủ A và B lần lượt bằng \( \frac{1}{3} \) và \( \frac{2}{5} \). Xác suất để cả hai xạ thủ A và B cùng bắn trúng bia là:
-
A.
\( \frac{13}{15} \).
-
B.
\( \frac{11}{15} \).
-
C.
\( \frac{3}{5} \).
-
D.
\( \frac{2}{15} \).
Từ một hộp gồm 13 quả cầu cân đối và đồng chất, trong đó có 8 quả cầu màu trắng và 5 quả cầu màu đen. Lấy ngẫu nhiên đồng thời 2 quả cầu từ hộp. Tính xác suất lấy được 2 quả cầu cùng màu.
-
A.
\( \frac{3}{13} \).
-
B.
\( \frac{20}{39} \).
-
C.
\( \frac{19}{39} \).
-
D.
\( \frac{17}{39} \).
Đạo hàm của hàm số \( y = \frac{1}{3}x^3 - x^2 + 1 \) là
-
A.
\( y' = x^2 - 2x \).
-
B.
\( y' = x^2 - 2x + 1 \).
-
C.
\( y' = x^3 - 2x \).
-
D.
\( y' = \frac{1}{3}x^2 - 2x \).
Tiếp tuyến của đồ thị hàm số \( y = x^2 + 4x - 5 \) tại điểm có hoành độ bằng 1 là
-
A.
\( y = 6x + 1 \).
-
B.
\( y = 6x + 6 \).
-
C.
\( y = 6x - 1 \).
-
D.
\( y = 6x - 6 \).
Khi thống kê điểm môn toán của 30 học sinh lớp 11, ta thu được mẫu số liệu ghép nhóm được cho ở bảng sau:

Nhóm chứa tứ phân vị thứ nhất là
-
A.
[2;4).
-
B.
[4;6).
-
C.
[6;8).
-
D.
[8;10).
Cho phương trình lượng giác \( 2\sin x = \sqrt{2} \) (1). Khi đó:
Phương trình tương đương với phương trình (1) là \( \sin x = \sin \frac{\pi}{4} \).
Phương trình (1) có nghiệm là: \( x = \frac{3\pi}{4} + k2\pi; x = \frac{\pi}{4} + k2\pi (k \in \mathbb{Z}) \).
Phương trình (1) có nghiệm dương nhỏ nhất bằng \( \frac{3\pi}{4} \).
Số nghiệm của phương trình (1) trong khoảng \( \left( -\frac{\pi}{2}; \frac{\pi}{2} \right) \) là hai nghiệm.
Cho bất phương trình: \( \log_{0,3}(2x + 1) \le \log_{0,3}(3x) \).
Điều kiện xác định của bất phương trình là \( x > -\frac{1}{2} \).
Bất phương trình tương đương với: \( 2x + 1 \le 3x \).
Tập nghiệm của bất phương trình là \( S = (0;1] \).
\( x = \frac{1}{2} \) thuộc miền nghiệm của bất phương trình đã cho.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với mặt phẳng (ABCD) và \( SA = a\sqrt{3} \).
\( SA \perp BD \).
\( (SAC) \perp (SBD) \).
Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng \( 30^\circ \).
Khoảng cách giữa hai đường thẳng AD và SB bằng \( \frac{a\sqrt{3}}{2} \).
Một vật chuyển động với vận tốc ban đầu là \( v_0 \) (m/s) sau đó dừng lại, phương trình quãng đường của vật là \( s = s(t) = -t^3 + 6t^2 + 15t \) trong đó t tính bằng giây và s tính bằng mét.
Vận tốc của vật tại thời điểm t = 2 s là v = 18 m/s.
Vận tốc của vật tại thời điểm t là \( v(t) = -3t^2 + 12t + 15 \) (m/s).
Vật đạt vận tốc lớn nhất tại thời điểm t = 2(s).
Vật dừng lại sau khoảng thời gian kể từ lúc bắt đầu chuyển động là t = 4s giây.
Một loại thuốc được dùng mỗi ngày một lần. Lúc đầu nồng độ thuốc trong máu của bệnh nhân tăng nhanh, nhưng mỗi liều kế tiếp có tác dụng ít hơn liều trước đó. Lượng thuốc trong máu ở ngày thứ nhất là 50mg, và mỗi ngày sau đó giảm chỉ còn một nửa so với ngày kể trước đó. Tính tổng lượng thuốc (tính bằng mg) trong máu của bệnh nhân sau khi dùng thuốc 10 ngày liên tiếp. (Kết quả được làm tròn đến hàng phần mười).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bằng 1. Hình chiếu của đỉnh S lên mặt phẳng (ABCD) là trung điểm H của AB. Góc tạo bởi SC và mặt phẳng (ABCD) bằng \(60^\circ\). Tính thể tích khối chóp S.ABCD. (Kết quả được làm tròn đến hàng phần trăm).
Một người cần sơn các mặt của một cái bục (trừ đáy lớn) để đặt một bức tượng. Bục có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn 1 m, cạnh bên và cạnh đáy nhỏ bằng 0,7 m. Tính tổng diện tích cần sơn. (Kết quả được làm tròn đến hàng phần trăm).
Giá trị còn lại của một chiếc xe theo thời gian khấu hao được xác định bởi công thức: \(V(t) = 15000e^{-0.15t}\) trong đó \(V(t)\) được tính bằng USD và \(t\) được tính bằng năm. Hỏi sau bao năm, giá trị còn lại của chiếc xe chỉ là 4518 USD? (Kết quả được làm tròn đến hàng đơn vị).
Hàm số \(f(x) = \frac{x}{\sqrt{9x^2 + 5} - 1}\). Tập nghiệm của bất phương trình \(f'(x) \geq 0\) là \(S = [a; b]\). Tính giá trị của biểu thức \(S = a^2 + b^2\). (Kết quả được làm tròn đến hàng phần mười).
Một hộp có 15 chiếc thẻ được đánh số lần lượt từ 1 đến 15. Chọn ngẫu nhiên 3 thẻ từ hộp đó. Tính xác suất để tổng 3 số ghi trên 3 thẻ đó là một số chia hết cho 3 (Kết quả được làm tròn đến hàng phần trăm).
Lời giải và đáp án
Rút gọn biểu thức \( T = \sin( \frac{\pi}{3}+x)-\sin( \frac{\pi}{3})-x \) ta được kết quả là
-
A.
\( T = \frac{\sqrt{3}}{2} \).
-
B.
\( T = \sin 2x \).
-
C.
\( T = \sqrt{3} \cos x \).
-
D.
\( T = \sin x \).
Đáp án : D
Sử dụng công thức cộng lượng giác:
\(\sin A - \sin B = 2 \cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)\).
\(T = \sin\left(\tfrac{\pi}{3} + x\right) - \sin\left(\tfrac{\pi}{3} - x\right) \)
\(= 2\cos\left(\tfrac{\pi}{3}\right)\sin(x) \)
\(= 2 \cdot \tfrac{1}{2} \cdot \sin x \)
\(= \sin x\).
Cho \( (u_n) \) là cấp số cộng có số hạng đầu bằng 2, công sai bằng 5. Tổng 10 số hạng đầu tiên của cấp số cộng đó bằng?
-
A.
-410.
-
B.
-205.
-
C.
245.
-
D.
-230.
Đáp án : C
Tổng $n$ số hạng đầu của cấp số cộng:
\(S_n = \frac{n}{2} \big(2u_1 + (n-1)d\).
Với $n = 10$:
$S_{10} = \frac{10}{2}\big(2 \cdot 2 + (10-1)\cdot 5\big) = 245$.
Cho hình chóp tứ giác S.ABCD . Gọi M, N lần lượt là trung điểm của SB và BD. Khẳng định nào sau đây đúng?
-
A.
\( MN \parallel (SAD) \).
-
B.
\( MN \parallel (SBC) \).
-
C.
\( MN \parallel (SAB) \).
-
D.
\( MN \parallel (SAC) \).
Đáp án : A
Sử dụng tính chất của đường trung bình trong tam giác.
Đưòng thẳng d song song với mặt phẳng (P) khi d song song với một đường thẳng d' thuộc (P) và d không thuộc (P).
Xét tam giác SBD có MN là đường trung bình, do. dó MN // SD, suy ra MN // (SAD).
Hàm số nào sau đây liên tục tại \( x = 1 \)?
-
A.
\( f(x) = \begin{cases} \frac{x^2 - 1}{x - 1} & \text{khi } x < 1 \\ 2x + 1 & \text{khi } x \ge 1 \end{cases} \).
-
B.
\( f(x) = \begin{cases} \frac{x^2 - 1}{x - 1} & \text{khi } x < 1 \\ 2x & \text{khi } x \ge 1 \end{cases} \).
-
C.
\( f(x) = \begin{cases} \frac{x^2 - 1}{x - 1} & \text{khi } x < 1 \\ 2x - 1 & \text{khi } x \ge 1 \end{cases} \).
-
D.
\( f(x) = \begin{cases} \frac{x^2 - 1}{x - 1} & \text{khi } x < 1 \\ x - 1 & \text{khi } x \ge 1 \end{cases} \).
Đáp án : B
Điều kiện để hàm số y = f(x) liên tục tại x = a:
f(a) tồn tại;
$\lim_{x \to a} f(x) $ tồn tại;
$\lim_{x \to a^+} f(x) = \lim_{x \to a^-} = f(a)$.
Xét từng đáp án:
A.
- \(f(1) = 2(1) + 1 = 3\).
- Với \(x < 1\): \(\frac{x^2 - 1}{x - 1} = \frac{(x-1)(x+1)}{x-1} = x + 1\) (với \(x \ne 1\)).
\(\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} (x + 1) = 2\).
- Với \(x \geq 1\): \(\lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} (2x + 1) = 3\).
\(\lim_{x \to 1^-} f(x) = 2 \ne 3 = \lim_{x \to 1^+} f(x)\) nên \(\lim_{x \to 1} f(x)\) không tồn tại.
→ Không liên tục tại \(x=1\).
B.
- \(f(1) = 2(1) = 2\).
- \(\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} (x + 1) = 2\).
- \(\lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} (2x) = 2\).
- \(\lim_{x \to 1} f(x) = 2 = f(1)\).
→ Liên tục tại \(x=1\).
C.
- \(f(1) = 2(1) - 1 = 1\).
- \(\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} (x + 1) = 2\).
- \(\lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} (2x - 1) = 1\).
- \(\lim_{x \to 1^-} f(x) = 2 \ne 1 = \lim_{x \to 1^+} f(x)\) nên \(\lim_{x \to 1} f(x)\) không tồn tại.
→ Không liên tục tại \(x=1\).
D.
- \(f(1) = 1 - 1 = 0\).
- \(\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} (x + 1) = 2\).
- \(\lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} (x - 1) = 0\).
- \(\lim_{x \to 1^-} f(x) = 2 \ne 0 = \lim_{x \to 1^+} f(x)\) nên \(\lim_{x \to 1} f(x)\) không tồn tại.
→ Không liên tục tại \(x=1\).
Cho biểu thức \(T = {x^{ - \frac{3}{4}}}\sqrt[4]{{{x^5}}}\) \((x > 0)\). Khẳng định nào sau đây đúng?
-
A.
\( T = x^{-\frac{1}{2}} \).
-
B.
\( T = x^{-2} \).
-
C.
\( T = x^{\frac{1}{2}} \).
-
D.
\( T = x^{2} \).
Đáp án : C
Áp dụng các công thức luỹ thừa.
\(T = x^{-\frac{3}{4}} \cdot x^{\frac{5}{4}} = x^{\frac{-3+5}{4}} = x^{\frac{2}{4}} = x^{\frac{1}{2}} \).
Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng 2a , cạnh bên bằng a. Tính số đo của góc nhị diện [A, B'C', A']
-
A.
\( 30^\circ \).
-
B.
\( 60^\circ \).
-
C.
\( 45^\circ \).
-
D.
\( 90^\circ \).
Đáp án : A
Cho góc nhị diện [P, d, Q]. Lấy O thuộc d, hai tia Ox, Oy lần lượt nằm trên hai nửa mặt phẳng (P), (Q) và cùng vuông góc với d. Khi đó góc xOy là góc phẳng nhị diện của góc nhị diện [P, d, Q].
Gọi M là trung điểm của B'C'.
Khi đó hai tam giác cân AB'C' và A'B'C' lần lượt có các đường cao là AM và A'M.
Góc nhị diện [A, B'C', A'] là góc AMA'. Xét tam giác vuông AMA' có:
\(\tan \widehat{AMA'} = \frac{AA'}{A'M} = \frac{a}{a\sqrt{3}} = \frac{\sqrt{3}}{3} \implies \widehat{AMA'} = 30^\circ\).
Cho hình chóp S.ABC , biết \( SA \perp (ABC) \) và tam giác ABC vuông tại A . Đường thẳng AB vuông góc với mặt phẳng nào sau đây?
-
A.
(SAB).
-
B.
(SAC).
-
C.
(SBC).
-
D.
(ABC).
Đáp án : B
Đường thẳng d vuông góc với mặt phẳng (P) nếu d vuông góc với hai đường thẳng cắt nhau thuộc (P).
Vì AB vuông góc với AC, AB vuông góc với SA (do SA vuông góc với (ABC)) nên AB vuông góc với (SAC).
Hai xạ thủ A và B cùng bắn súng một cách độc lập. Xác suất bắn trúng bia của hai xạ thủ A và B lần lượt bằng \( \frac{1}{3} \) và \( \frac{2}{5} \). Xác suất để cả hai xạ thủ A và B cùng bắn trúng bia là:
-
A.
\( \frac{13}{15} \).
-
B.
\( \frac{11}{15} \).
-
C.
\( \frac{3}{5} \).
-
D.
\( \frac{2}{15} \).
Đáp án : D
Áp dụng công thức nhân xác suất của hai biến cố độc lập.
Gọi:
- \(A\) là biến cố "Xạ thủ A bắn trúng bia".
- \(B\) là biến cố "Xạ thủ B bắn trúng bia".
Theo đề bài:
- \(P(A) = \frac{1}{3}\).
- \(P(B) = \frac{2}{5}\).
Do hai xạ thủ bắn độc lập, nên biến cố "Cả hai xạ thủ A và B cùng bắn trúng bia" là \(A \cap B\).
Xác suất cần tính là:
\(P(A \cap B) = P(A) \cdot P(B) = \frac{1}{3} \cdot \frac{2}{5} = \frac{2}{15}\).
Từ một hộp gồm 13 quả cầu cân đối và đồng chất, trong đó có 8 quả cầu màu trắng và 5 quả cầu màu đen. Lấy ngẫu nhiên đồng thời 2 quả cầu từ hộp. Tính xác suất lấy được 2 quả cầu cùng màu.
-
A.
\( \frac{3}{13} \).
-
B.
\( \frac{20}{39} \).
-
C.
\( \frac{19}{39} \).
-
D.
\( \frac{17}{39} \).
Đáp án : C
Áp dụng công thức tính số tổ hợp, quy tắc cộng và quy tắc nhân.
Tổng số cách lấy ngẫu nhiên 2 quả cầu từ 13 quả là:
\(n(\Omega) = C_{13}^2 = \frac{13!}{2!(13-2)!} = \frac{13 . 12}{2} = 78\).
Gọi biến cố A: "Lấy được 2 quả cầu cùng màu".
- Số cách lấy 2 quả cầu màu trắng từ 8 quả:
\(C_8^2 = \frac{8!}{2!(8-2)!} = \frac{8 . 7}{2} = 28\).
- Số cách lấy 2 quả cầu màu đen từ 5 quả:
\(C_5^2 = \frac{5!}{2!(5-2)!} = \frac{5 . 4}{2} = 10\).
Số kết quả thuận lợi cho biến cố A là:
\(n(A) = C_8^2 + C_5^2 = 28 + 10 = 38\).
Xác suất cần tính là:
\(P(A) = \frac{n(A)}{n(\Omega)} = \frac{38}{78} = \frac{19}{39}\).
Đạo hàm của hàm số \( y = \frac{1}{3}x^3 - x^2 + 1 \) là
-
A.
\( y' = x^2 - 2x \).
-
B.
\( y' = x^2 - 2x + 1 \).
-
C.
\( y' = x^3 - 2x \).
-
D.
\( y' = \frac{1}{3}x^2 - 2x \).
Đáp án : A
Sử dụng công thức đạo hàm của hàm số luỹ thừa.
\(y' = \frac{1}{3} \cdot 3x^2 - 2x + 0 = x^2 - 2x\).
Tiếp tuyến của đồ thị hàm số \( y = x^2 + 4x - 5 \) tại điểm có hoành độ bằng 1 là
-
A.
\( y = 6x + 1 \).
-
B.
\( y = 6x + 6 \).
-
C.
\( y = 6x - 1 \).
-
D.
\( y = 6x - 6 \).
Đáp án : D
Phương trình tiếp tuyến của đồ thị hàm số \(y = f(x)\) tại điểm có hoành độ \(x_0\) có dạng:
\(y = f'(x_0)(x - x_0) + f(x_0)\).
Trong đó:
- \(f'(x_0)\) là đạo hàm của hàm số tại \(x_0\) (hệ số góc của tiếp tuyến),
- \(f(x_0)\) là giá trị của hàm số tại \(x_0\).
Hàm số: \( y = x^2 + 4x - 5 \).
Đạo hàm: \( y' = 2x + 4 \).
Tại điểm có hoành độ \( x = 1 \):
- Tung độ: \( y(1) = 1^2 + 4 \cdot 1 - 5 = 0 \).
- Hệ số góc: \( y'(1) = 2 \cdot 1 + 4 = 6 \).
Phương trình tiếp tuyến tại điểm \( (1; 0) \) với hệ số góc \( k = 6 \):
\(y - 0 = 6(x - 1) \Rightarrow y = 6x - 6\).
Khi thống kê điểm môn toán của 30 học sinh lớp 11, ta thu được mẫu số liệu ghép nhóm được cho ở bảng sau:

Nhóm chứa tứ phân vị thứ nhất là
-
A.
[2;4).
-
B.
[4;6).
-
C.
[6;8).
-
D.
[8;10).
Đáp án : B
Tìm cỡ mẫu, lập bảng tần số tích luỹ.
Cỡ mẫu: \(n = 2 + 4 + 4 + 13 + 7 = 30\).
Tứ phân vị thứ nhất \( Q_1 \) là giá trị tại vị trí:
\(\frac{n}{4} = \frac{30}{4} = 7,5\).
Do đó, \( Q_1 \) nằm ở nhóm chứa học sinh thứ 7,5.
Vị trí \( 7,5 \) thuộc nhóm có tần số tích lũy đầu tiên lớn hơn hoặc bằng 7,5.
Nhóm [2;4) có tần số tích lũy là 6 < 7,5.
Nhóm [4;6) có tần số tích lũy là 10 ≥ 7,5.
Vậy nhóm chứa tứ phân vị thứ nhất là [4;6).
Cho phương trình lượng giác \( 2\sin x = \sqrt{2} \) (1). Khi đó:
Phương trình tương đương với phương trình (1) là \( \sin x = \sin \frac{\pi}{4} \).
Phương trình (1) có nghiệm là: \( x = \frac{3\pi}{4} + k2\pi; x = \frac{\pi}{4} + k2\pi (k \in \mathbb{Z}) \).
Phương trình (1) có nghiệm dương nhỏ nhất bằng \( \frac{3\pi}{4} \).
Số nghiệm của phương trình (1) trong khoảng \( \left( -\frac{\pi}{2}; \frac{\pi}{2} \right) \) là hai nghiệm.
Phương trình tương đương với phương trình (1) là \( \sin x = \sin \frac{\pi}{4} \).
Phương trình (1) có nghiệm là: \( x = \frac{3\pi}{4} + k2\pi; x = \frac{\pi}{4} + k2\pi (k \in \mathbb{Z}) \).
Phương trình (1) có nghiệm dương nhỏ nhất bằng \( \frac{3\pi}{4} \).
Số nghiệm của phương trình (1) trong khoảng \( \left( -\frac{\pi}{2}; \frac{\pi}{2} \right) \) là hai nghiệm.
Sử dụng phép biến đổi tương đương và công thức nghiệm của phương trình lượng giác cơ bản.
a) Đúng. Vì \(\sin \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\) nên \((1) \Leftrightarrow \sin x = \frac{{\sqrt 2 }}{2} \Leftrightarrow \sin x = \sin \frac{\pi }{4}\).
b) Đúng. \((1) \Leftrightarrow \sin x = \sin \frac{\pi }{4} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \pi - \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \frac{{3\pi }}{4} + k2\pi \end{array} \right.\) \(\left( {k \in \mathbb{Z}} \right)\).
c) Sai. Phương trình có nghiệm dương nhỏ nhất là \(x = \frac{\pi }{4}\).
d) Sai. Số nghiệm của (1) trong \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) là một nghiệm \(x = \frac{\pi }{4}\).
Cho bất phương trình: \( \log_{0,3}(2x + 1) \le \log_{0,3}(3x) \).
Điều kiện xác định của bất phương trình là \( x > -\frac{1}{2} \).
Bất phương trình tương đương với: \( 2x + 1 \le 3x \).
Tập nghiệm của bất phương trình là \( S = (0;1] \).
\( x = \frac{1}{2} \) thuộc miền nghiệm của bất phương trình đã cho.
Điều kiện xác định của bất phương trình là \( x > -\frac{1}{2} \).
Bất phương trình tương đương với: \( 2x + 1 \le 3x \).
Tập nghiệm của bất phương trình là \( S = (0;1] \).
\( x = \frac{1}{2} \) thuộc miền nghiệm của bất phương trình đã cho.
Giải bất phương trình logarit. Lưu ý cơ số.
a) Sai. Điều kiện xác định: \(\left\{ \begin{array}{l}2x + 1 > 0\\3x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - \frac{1}{2}\\x > 0\end{array} \right. \Leftrightarrow x > 0\).
b) Sai. Bất phương trình tương đương với \(2x + 1 \ge 3x\) vì cơ số 0,3 < 1 (cơ số < 1 thì bất phương trình đổi dấu).
c) Đúng. \(2x + 1 \ge 3x \Leftrightarrow x \le 1\). Vậy tập nghiệm là \(S = (0;1]\).
d) Đúng. \(x = \frac{1}{2} \in (0;1]\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với mặt phẳng (ABCD) và \( SA = a\sqrt{3} \).
\( SA \perp BD \).
\( (SAC) \perp (SBD) \).
Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng \( 30^\circ \).
Khoảng cách giữa hai đường thẳng AD và SB bằng \( \frac{a\sqrt{3}}{2} \).
\( SA \perp BD \).
\( (SAC) \perp (SBD) \).
Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng \( 30^\circ \).
Khoảng cách giữa hai đường thẳng AD và SB bằng \( \frac{a\sqrt{3}}{2} \).
a) Sử dụng tính chất của đường thẳng vuông góc với mặt phẳng.
b) Mặt phẳng (P) vuông góc với mặt phẳng (Q) nếu (P) chứa đường thẳng d vuông góc với (Q).
c) Góc giữa đường thẳng d và mặt phẳng (P) là góc giữa d và hình chiếu d' của nó trên (P).
d) Đưa về tính khoảng cách từ một điểm đến một mặt phẳng.
a) Đúng. Vì \(SA \bot (ABCD) \Rightarrow SA \bot BD\).
b) Đúng. Vì ABCD là hình vuông nên \(AC \bot BD\).
Ta có \(\left\{ \begin{array}{l}AC \bot BD\\SA \bot BD\end{array} \right. \Rightarrow BD \bot (SAC) \Rightarrow (SBD) \bot (SAC)\).
c) Sai. A là hình chiếu của S trên (ABCD) nên AB là hình chiếu của SB trên (ABCD).
Do đó góc giữa SB và (SBCD) là góc giữa SB và AB, hay \(\widehat {SBA}\).
\(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{2} = \sqrt 3 \Rightarrow \widehat {SBA} = {60^o}\).
d) Đúng. Có AD // BC nên AD // (SBC), do đó:
\(d\left( {AD,SB} \right) = d\left( {AD,(SBC)} \right) = d\left( {A,(SBC)} \right) = d\left( {A,SB} \right)\) là đường cao h kẻ từ A của tam giác SAB.
\(h = \sqrt {\frac{{SA.AB}}{{S{A^2} + A{B^2}}}} = \sqrt {\frac{{{{\left( {a\sqrt 3 } \right)}^2}.{a^2}}}{{{{\left( {a\sqrt 3 } \right)}^2} + {a^2}}}} = \frac{{a\sqrt 3 }}{2}\).
Một vật chuyển động với vận tốc ban đầu là \( v_0 \) (m/s) sau đó dừng lại, phương trình quãng đường của vật là \( s = s(t) = -t^3 + 6t^2 + 15t \) trong đó t tính bằng giây và s tính bằng mét.
Vận tốc của vật tại thời điểm t = 2 s là v = 18 m/s.
Vận tốc của vật tại thời điểm t là \( v(t) = -3t^2 + 12t + 15 \) (m/s).
Vật đạt vận tốc lớn nhất tại thời điểm t = 2(s).
Vật dừng lại sau khoảng thời gian kể từ lúc bắt đầu chuyển động là t = 4s giây.
Vận tốc của vật tại thời điểm t = 2 s là v = 18 m/s.
Vận tốc của vật tại thời điểm t là \( v(t) = -3t^2 + 12t + 15 \) (m/s).
Vật đạt vận tốc lớn nhất tại thời điểm t = 2(s).
Vật dừng lại sau khoảng thời gian kể từ lúc bắt đầu chuyển động là t = 4s giây.
a) Tìm v(t) = s'(t). Tính v(2).
b) Tìm v(t) = s'(t).
c) Lập bảng biến thiên của hàm số v(t).
d) Tìm t sao cho v(t) = 0.
a) Sai. \(v(t) = s'(t) = - 3{t^2} + 12t + 15 \Rightarrow v(2) = - {3.2^2} + 12.2 + 15 = 27\).
b) Đúng. \(v(t) = s'(t) = - 3{t^2} + 12t + 15\).
c) Đúng. \(v'(t) = - 6t + 12 = 0 \Leftrightarrow t = 2\).
Bảng biến thiên:
Vậy vận tốc đạt lớn nhất tại thời điểm t = 2.
d) Sai. Vật dừng lại thì v = 0, khi đó \( - 3{t^2} + 12t + 15 = 0 \Leftrightarrow t = - 1 \vee t = 5\).
Vì t > 0 nên loại t = 1. Vậy vật dừng dừng lại sau khoảng thời gian là 5 giây.
Một loại thuốc được dùng mỗi ngày một lần. Lúc đầu nồng độ thuốc trong máu của bệnh nhân tăng nhanh, nhưng mỗi liều kế tiếp có tác dụng ít hơn liều trước đó. Lượng thuốc trong máu ở ngày thứ nhất là 50mg, và mỗi ngày sau đó giảm chỉ còn một nửa so với ngày kể trước đó. Tính tổng lượng thuốc (tính bằng mg) trong máu của bệnh nhân sau khi dùng thuốc 10 ngày liên tiếp. (Kết quả được làm tròn đến hàng phần mười).
Áp dụng công thức tính tổng n số hạng đầu của cấp số nhân.
Lượng thuốc ở ngày thứ nhất là 50 mg.
Lượng thuốc ở ngày thứ hai là \(50.\frac{1}{2} = 25\) mg.
Lượng thuốc ở ngày thứ ba là \(50.{\left( {\frac{1}{2}} \right)^2} = \frac{{25}}{2}\) mg.
…
Lượng thuốc ở ngày thứ n là \(50.{\left( {\frac{1}{2}} \right)^{n - 1}}\) mg.
Lượn thuốc mỗi ngày lập thành cấp số nhân với số hạng đầu \({u_1} = 50\), công bội \(q = \frac{1}{2}\).
Tổng lượng thuốc khi dùng 10 ngày liên tiếp là:
\({S_{10}} = {u_1}.\frac{{1 - {q^{10}}}}{{1 - q}} = 50.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^{10}}}}{{1 - \frac{1}{2}}} = \frac{{25575}}{{256}} \approx 99,9\) (mg).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bằng 1. Hình chiếu của đỉnh S lên mặt phẳng (ABCD) là trung điểm H của AB. Góc tạo bởi SC và mặt phẳng (ABCD) bằng \(60^\circ\). Tính thể tích khối chóp S.ABCD. (Kết quả được làm tròn đến hàng phần trăm).
Góc tạo bởi SC và mặt phẳng (ABCD), từ đó sử dụng hệ thức lượng trong tam giác vuông và định lí Pythagore để tìm chiều cao khối chóp.
Áp dụng công thức tính thể tích khối chóp: $S=\dfrac{1}{3}Bh$.
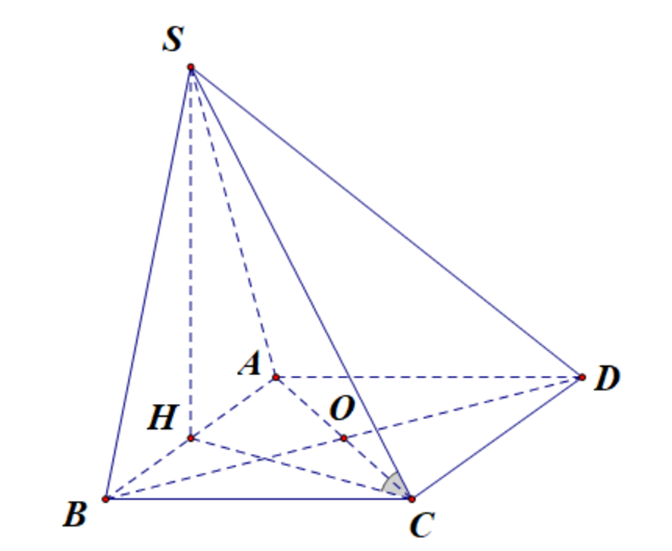
Hình chiếu vuông góc của S lên (ABCD) là H, do đó hình chiếu vuông góc của SC lên (ABCD) là HC. Góc tạo bởi SC và (ABCD) là góc giữa SC và HC, hay \(\widehat {SCH} = {60^o}\).
Xét tam giác HBC vuông tại B:
\(HC = \sqrt {B{C^2} + B{H^2}} = \sqrt {{1^2} + {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 5 }}{2}\).
Xét tam giác SHC vuông tại H:
\(\tan \widehat {SCH} = \frac{{SH}}{{HC}} \Leftrightarrow SH = HC\tan \widehat {SCH} = \frac{{\sqrt 5 }}{2}.\tan {60^o} = \frac{{\sqrt {15} }}{2}\).
Thể tích khối chóp là:
\(V = \frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}.\frac{{\sqrt {15} }}{2}{.1^2} = \frac{{\sqrt {15} }}{6} \approx 0,65\).
Một người cần sơn các mặt của một cái bục (trừ đáy lớn) để đặt một bức tượng. Bục có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn 1 m, cạnh bên và cạnh đáy nhỏ bằng 0,7 m. Tính tổng diện tích cần sơn. (Kết quả được làm tròn đến hàng phần trăm).
Tính diện tích đáy nhỏ và diện tích 4 mặt bên là hình thang.
Xét một mặt của hình chóp cụt tứ giác đều giả sử là hình thang cân $ABCD$, chiều cao $AH$ ta có:

$DH = 0,15$ (m).
$AH = \sqrt{0,7^2 - 0,15^2} = \frac{\sqrt{187}}{20}$ (m).
Diện tích hình thang $ABCD$ là:
$S_{ABCD} = \frac{(1+0,7)\sqrt{187}}{2.20} = \frac{17\sqrt{187}}{400}$ $(m^2)$.
Diện tích mặt đáy nhỏ là $0,7^2 = 0,49$ $(m^2)$.
Tổng diện tích cần sơn là:
$\frac{17\sqrt{187}}{400} \cdot 4 + 0,49 \approx 2,81$ $(m^2)$.
Giá trị còn lại của một chiếc xe theo thời gian khấu hao được xác định bởi công thức: \(V(t) = 15000e^{-0.15t}\) trong đó \(V(t)\) được tính bằng USD và \(t\) được tính bằng năm. Hỏi sau bao năm, giá trị còn lại của chiếc xe chỉ là 4518 USD? (Kết quả được làm tròn đến hàng đơn vị).
Giải phương trình mũ \(15000{e^{ - 0,15t}} = 4518\).
\(15000{e^{ - 0,15t}} = 4518 \Leftrightarrow {e^{ - 0,15t}} = \frac{{753}}{{2500}}\)
\( \Leftrightarrow \ln \frac{{753}}{{2500}} = - 0,15t \Leftrightarrow t = - \frac{{20}}{3}\ln \frac{{753}}{{2500}} \approx 8\).
Vậy sau 8 năm thì giá trị còn lại của chiếc xe là 4518 USD.
Hàm số \(f(x) = \frac{x}{\sqrt{9x^2 + 5} - 1}\). Tập nghiệm của bất phương trình \(f'(x) \geq 0\) là \(S = [a; b]\). Tính giá trị của biểu thức \(S = a^2 + b^2\). (Kết quả được làm tròn đến hàng phần mười).
Áp dụng các quy tắc tính đạo hàm và giải bất phương trình chứa dấu căn.
Tập xác định: \(D = \mathbb{R}\).
\(f'(x) = \frac{{x'\left( {\sqrt {9{x^2} + 5} - 1} \right) - x.\left( {\sqrt {9{x^2} + 5} - 1} \right)'}}{{{{\left( {\sqrt {9{x^2} + 5} - 1} \right)}^2}}}\)
\( = \frac{{\sqrt {9{x^2} + 5} - 1 - \frac{{9{x^2}}}{{\sqrt {9{x^2} + 5} }}}}{{{{\left( {\sqrt {9{x^2} + 5} - 1} \right)}^2}}}\).
\(f'(x) \ge 0 \Leftrightarrow \sqrt {9{x^2} + 5} - 1 - \frac{{9{x^2}}}{{\sqrt {9{x^2} + 5} }} \ge 0\)
\( \Leftrightarrow \frac{{9{x^2} + 5}}{{\sqrt {9{x^2} + 5} }} - 1 - \frac{{9{x^2}}}{{\sqrt {9{x^2} + 5} }} \ge 0\)
\( \Leftrightarrow \frac{5}{{\sqrt {9{x^2} + 5} }} \ge 1 \Leftrightarrow 5 \ge \sqrt {9{x^2} + 5} \) (cả tử và mẫu đều dương nên ta nhân chéo)
\( \Leftrightarrow 25 \ge 9{x^2} + 5 \Leftrightarrow 9{x^2} \le 20 \Leftrightarrow {x^2} \le \frac{{20}}{9} \Leftrightarrow - \sqrt {\frac{{20}}{9}} \le x \le \sqrt {\frac{{20}}{9}} \).
Do đó \(S = \left[ { - \sqrt {\frac{{20}}{9}} ;\sqrt {\frac{{20}}{9}} } \right]\).
Vậy \({a^2} + {b^2} = \frac{{20}}{9} + \frac{{20}}{9} = \frac{{40}}{9} \approx 4,4\).
Một hộp có 15 chiếc thẻ được đánh số lần lượt từ 1 đến 15. Chọn ngẫu nhiên 3 thẻ từ hộp đó. Tính xác suất để tổng 3 số ghi trên 3 thẻ đó là một số chia hết cho 3 (Kết quả được làm tròn đến hàng phần trăm).
Áp dụng công thức tính số tổ hợp, quy tắc cộng và quy tắc nhân xác suất.
Rút ngẫu nhiên 3 thẻ trong 15 thẻ có \(C_{15}^3\) cách \( \Rightarrow n(\Omega ) = C_{15}^3 = 455\).
Gọi X là biến cố “Tổng ba số ghi trên ba thẻ rút được”.
Khi đó \(\left\{ {\begin{array}{*{20}{l}}{1 \le x,y \le 15}\\{x + y + z:3}\end{array}} \right.\)
Gọi N1 là nhóm các số chia hết cho 3. N1 gồm 5 số (3; 6; 9; 12; 15).
Gọi N2 là nhóm các số chia 3 dư 1. N2 gồm 5 số (1; 4; 7; 10; 13).
Gọi N3 là nhóm các số chia 3 dư 2. N3 gồm 5 số (2; 5; 8; 11; 14).
TH1: 2 số x, y, z thuộc cùng 1 loại N1, N2 hoặc N3 \( \Rightarrow \) Có \(C_5^3 + C_5^3 + C_5^3 = 30\) cách.
TH2: 3 số x, y, z mỗi số thuộc 1 loại \( \Rightarrow \) Có \(C_5^1.C_5^1.C_5^1 = 125\) cách.
\( \Rightarrow \) Số kết quả thuận lợi cho biến cố X là \(n(X) = 30 + 125 = 155\).
Vậy \(P = \frac{{n(X)}}{{n(\Omega )}} = \frac{{31}}{{91}} \approx 0,34\).










Danh sách bình luận