Lý thuyết Phép chia đa thức một biến Toán 7

Chia đa thức cho đa thức, trường hợp chia hết

Đặt tính chia:

Bước 1: Đặt tính chia tương tự chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.

Bước 2: Lấy A trừ đi tích của B với thương ở bước 1, được dư thứ nhất.

Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B.

Bước 4: Lấy dư thứ nhất trừ đi tích của B với thương ở bước 3, ta thu được dư thứ 2.

Bước 5: Làm tương tự như trên, đến khi dư bằng 0 thì kết thúc.

Ví dụ:

Tính \(\left(2x^4 - x^3 + 2x - 1\right) : \(left( x^2 - x + 1\right)

- Lấy \(2x^4 : x^2\) được \(2x^2\), ta viết \(2x^2\) vào thương. Sau đó nhân lần lượt \(2x^2\) với các hạng tử của đa thức chia, ta được \(2x^4 - 2x^3 + 2x^2\). Lấy đa thức bị chia trừ đi đa thức \(2x^4 - 2x^3 + 2x^2\), được \(x^3 - 2x^2 + 2x - 1\).

- Lấy \(x^3 : x^2\) được \(x\), ta viết \(+ x\) vào thương. Sau đó nhân lần lượt \(x\) với các hạng tử của đa thức chia, ta được \(x^3 - x^2 + x\). Lấy đa thức \(x^3 - 2x^2 + 2x - 1\) trừ đi đa thức \(x^3 - x^2 + x\), được \(-x^2 + x - 1\).

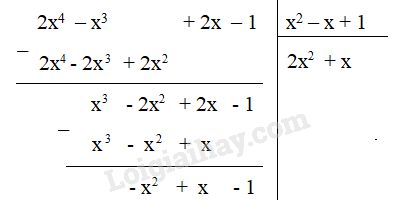
- Lấy \(-x^2 : x^2\) được \(-1\), ta viết \(-1\) vào thương. Sau đó nhân lần lượt \(-1\) với các hạng tử của đa thức chia, ta được \(-x^2 + x - 1\). Lấy đa thức \(-x^2 + x - 1\) trừ đi đa thức \(-x^2 + x - 1\), được \(0\).

Vậy \(\left(2x^4 - x^3 + 2x - 1\right) : \left( x^2 - x + 1\right) = 2x^2 + x - 1\)