Cách xét tính biến thiên của hàm số mũ, hàm số logarit - Toán 11

Hàm số mũ \(y = {a^x}\) \(\left( {1 \ne a > 0} \right)\):

+ Nếu a > 1 thì hàm số đồng biến trên \(\mathbb{R}\).

+ Nếu 0 < a < 1 thì hàm số nghịch biến trên \(\mathbb{R}\).

Hàm số logarit \(y = {\log _a}x\) \(\left( {1 \ne a > 0} \right)\):

+ Nếu a > 1 thì hàm số đồng biến trên \(\left( {0; + \infty } \right)\).

+ Nếu 0 < a < 1 thì hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).

1) Xét sự biến thiên của các hàm số:

a) \(y = {5^x}\);

b) \(y = {\left( {\frac{1}{2}} \right)^x}\);

c) \(y = {\left( {\pi  - \sqrt 2 } \right)^x}\);

d) \(y = {\left( {6 - \sqrt 5 } \right)^x}\).

Giải:

a) Vì 5 > 1 nên hàm số \(y = {5^x}\) đồng biến trên \(\mathbb{R}\).

b) Vì \(0 < \frac{1}{2} < 1\) nên hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) nghịch biến trên \(\mathbb{R}\).

c) Vì \(\pi  - \sqrt 2  > 1\) nên hàm số \(y = {\left( {\pi  - \sqrt 2 } \right)^x}\) đồng biến trên \(\mathbb{R}\).

d) Vì \(6 - \sqrt 5  > 1\) nên hàm số \(y = {\left( {6 - \sqrt 5 } \right)^x}\) đồng biến trên \(\mathbb{R}\).

2) Xét sự biến thiên của các hàm số:

a) \(y = \ln x\);

b) \(y = {\log _{1 - \sqrt {\frac{{2018}}{{2019}}} }}x\);

c) \(y = {\log _\pi }x\);

d) \(y = {\log _{4 - \sqrt 3 }}x\).

Giải:

a) Vì e > 1 nên hàm số \(y = \ln x\) đồng biến trên \(\left( {0; + \infty } \right)\).

b) Vì \(0 < \frac{1}{2} < 1\) nên hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) nghịch biến trên \(\left( {0; + \infty } \right)\).

c) Vì \(\pi  - \sqrt 2  > 1\) nên hàm số \(y = {\left( {\pi  - \sqrt 2 } \right)^x}\) đồng biến trên \(\left( {0; + \infty } \right)\).

d) Vì \(6 - \sqrt 5  > 1\) nên hàm số \(y = {\left( {6 - \sqrt 5 } \right)^x}\) đồng biến trên \(\left( {0; + \infty } \right)\).

3) Cho số thực \(a \in (0;1)\). Đồ thị hàm số \(y = {\log _a}x\) là đường cong nào dưới đây?

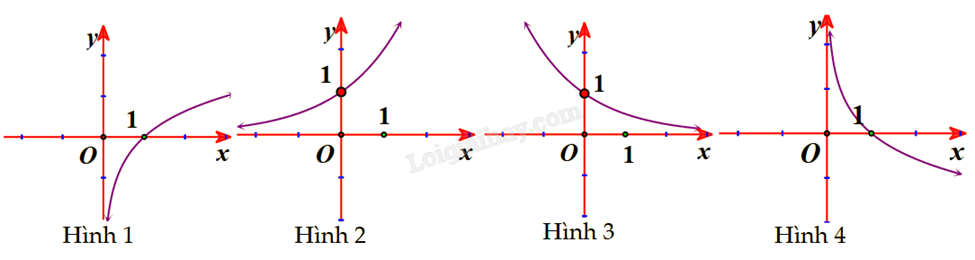
Giải:

Đồ thị hàm số \(y = {\log _a}x\) là đường cong nằm bên phải trục tung và đi qua điểm (1;0).

Vì \(a \in (0;1)\) nên hàm số nghịch biến, suy ra đồ thị hàm số là Hình 4.