Cách nhận dạng đồ thị và tìm cơ số hàm số mũ, hàm số logarit - Toán 11

Đồ thị hàm số mũ \(y = {a^x}\) \(\left( {1 \ne a > 0} \right)\):

- Luôn nằm trên trục hoành Ox.

- Luôn đi qua điểm (0;1).

- Cơ số:

+ a > 1: Đường cong càng gần Oy thì cơ số càng lớn.

+ 0 < a < 1: Đường cong càng gần Oy thì cơ số càng bé.

Đồ thị hàm số logarit \(y = {\log _a}x\) \(\left( {1 \ne a > 0} \right)\):

Đồ thị hàm số mũ \(y = {a^x}\) \(\left( {1 \ne a > 0} \right)\):

- Luôn nằm bên phải trục tung Oy.

- Luôn đi qua điểm (1;0).

- Cơ số:

+ a > 1: Đường cong càng gần Ox thì cơ số càng lớn.

+ 0 < a < 1: Đường cong càng gần Ox thì cơ số càng bé.

1) Cho các hàm số \(y = {a^x}\), \(y = {b^x}\), \(y = {c^x}\) lần lượt có đồ thị như hình vẽ. Hãy so sánh a, b, c.

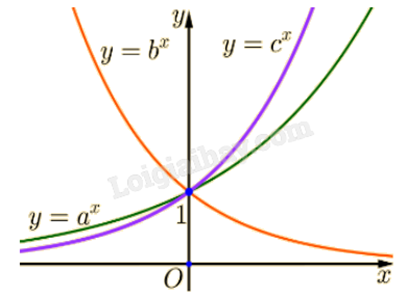
Giải:

Thấy \(y = {b^x}\) là hàm số mũ nghịch biến nên 0 < b < 1.

\(y = {a^x}\), \(y = {c^x}\) là hàm số mũ đồng biến nên a, c > 1.

Vì đồ thị \(y = {c^x}\) gần trục Oy hơn \(y = {a^x}\) nên a > c.

Từ đó c > a > b.

2) Cho các hàm số \(y = {\left( {\sqrt 3 } \right)^x}\), \(y = {\left( {\frac{1}{2}} \right)^x}\), \(y = {\left( {\sqrt 2 } \right)^x}\) và \(y = {\left( {\frac{1}{3}} \right)^x}\). Đồ thị hàm số dưới đây là của hàm số nào đã cho?

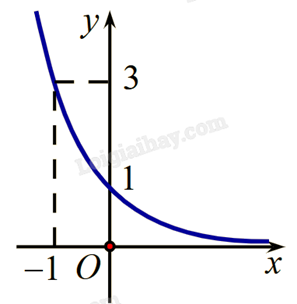
Giải:

Dựa vào đồ thị, hàm số nghịch biến nên loại \(y = {\left( {\sqrt 3 } \right)^x}\), \(y = {\left( {\sqrt 2 } \right)^x}\).

Đồ thị đi qua điểm (-1;3) nên đồ thị đã cho là của hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\).

3) Cho các hàm số \(y = {\log _2}x\), \(y = {\log _{\frac{1}{2}}}x\), \(y = {\left( {\frac{1}{2}} \right)^x}\) và \(y = {2^x}\). Đồ thị hàm số dưới đây là của hàm số nào đã cho?

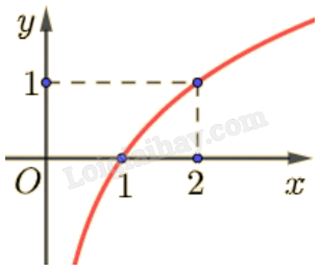
Giải:

Đây là dạng đồ thị của hàm số \(y = {\log _a}x\) nên loại \(y = {\left( {\frac{1}{2}} \right)^x}\) và \(y = {2^x}\).

Hàm số đồng biến loại \(y = {\log _{\frac{1}{2}}}x\).

Đồ thị đi qua điểm \((2;1)\) nên đồ thị đã cho là đồ thị của hàm số \(y = {\log _2}x\).

4) Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \(y = {\log _a}x\), \(y = {\log _b}x\), \(y = {\log _c}x\) được cho trong hình vẽ bên. So sánh các số a, b, c.

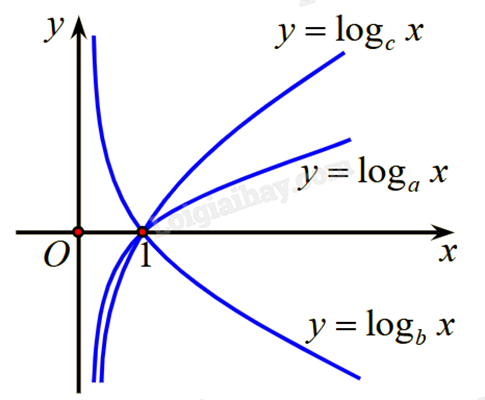
Giải:

Dựa vào đồ thị, ta thấy hàm số \(y = {\log _b}x\) nghịch biến trên \((0; + \infty ) \Rightarrow 0 < b < 1\).

Quan sát đồ thị ta thấy hàm số \(y = {\log _a}x\), \(y = {\log _c}x\) đồng biến trên \((0; + \infty ) \Rightarrow a,c > 1\).

Xét \(x > 1:{\log _c}x > {\log _a}x \Rightarrow {\log _c}x > \frac{1}{{{{\log }_x}a}} \Rightarrow {\log _c}x \cdot {\log _x}a > 1 \Leftrightarrow {\log _c}a > 1 \Leftrightarrow a > c\).

Suy ra \(b < c < a\).

5) Cho đồ thị hàm số \(y = {a^x}\), \(y = {b^x}\), \(y = {\log _c}x\) như hình vẽ. Tìm mối liên hệ của a, b, c.

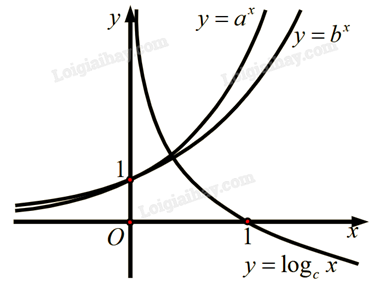
Giải:

Nhận xét hàm số \(y = {\log _c}x\) nghịch biến nên \(c < 1\).

Hàm số \(y = {a^x}\), \(y = {b^x}\) đồng biến nên \(a > 1\), \(b > 1\). 

Xét tại \(x = 1\) đồ thị hàm số \(y = {a^x}\) có tung độ lớn hơn tung độ của đồ thị hàm số \(y = {b^x}\) nên \(a > b\). Vậy \(a > b > 1 > c\).