Cách xác định vị trí của điểm so với mặt cầu - Toán 12

Cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\), \(B\left( {{x_B};{y_B};{z_B}} \right)\). Độ dài vecto \(\overrightarrow {AB} \) hay khoảng cách từ A đến B là: \(\left| {\overrightarrow {AB} } \right| = AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).

Ví dụ minh hoạ:

1) Trong không gian Oxyz, cho hai điểm A(2;1;3), B(1;-1;5). Tính độ dài đoạn thẳng AB.

Giải:

\(AB = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2} + {{({z_B} - {z_A})}^2}} {\rm{\;}} = \sqrt {{{(1 - 2)}^2} + {{( - 1 - 1)}^2} + {{(5 - 3)}^2}} {\rm{\;}} = 3\).

2) Trong không gian Oxy, cho điểm A(-5;2;3) và B là điểm đối xứng với A qua trục Oy. Tính độ dài đoạn thẳng AB.

Giải:

B đối xứng với A qua Oy nên B(5;2;-3).

\(AB = \sqrt {{{(5 + 5)}^2} + {{(2 - 2)}^2} + {{( - 3 - 3)}^2}} {\rm{\;}} = 2\sqrt {34} \).

Cho mặt cầu S(I;r) và điểm M bất kì trong không gian.

- Nếu IM = r thì M nằm trên mặt cầu S(I;r).

- Nếu IM < r thì M nằm ngoài mặt cầu S(I;r).

- Nếu IM > r thì M nằm ngoài mặt cầu S(I;r).

Xét mặt cầu và các điểm như hình:

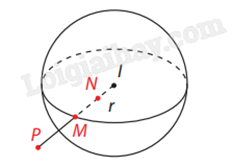
- Điểm M nằm trên mặt cầu (S).
- Điểm N nằm trong mặt cầu (S).
- Điểm P nằm ngoài mặt cầu (S).

Ví dụ minh hoạ:

Trong không gian với hệ toạ độ Oxyz, cho mặt cầu tâm I(-2;1;5) bán kính 3. Các điểm A(10;1;2), B(0;1;4), C(0;3;4) nằm trong, nằm trên hay nằm ngoài mặt cầu đó?

Giải:

Do \(IA = \sqrt {{{\left( {10 - ( - 2)} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {2 - 5} \right)}^2}}  = \sqrt {153}  > 3\) nên điểm A(10;1;2) nằm ngoài mặt cầu đó.

Do \(IB = \sqrt {{{\left( {0 - ( - 2)} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}}  = \sqrt 5  < 3\) nên điểm B(0;1;4) nằm trong mặt cầu đó.

Do \(IC = \sqrt {{{\left( {0 - ( - 2)} \right)}^2} + {{\left( {3 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}}  = \sqrt 9  = 3\) nên điểm C(0;3;4) nằm trên mặt cầu đó.