Cách tính thể tích khối chóp - Toán 11

Trong mặt phẳng (P), cho đa giác \({A_1}{A_2}...{A_n}\) \(\left( {n \ge 3} \right)\). Lấy điểm S nằm ngoài (P). Nối S với các đỉnh \({A_1}\), \({A_2}\), …, \({A_n}\), ta được n tam giác: \(S{A_1}{A_2}\), \(S{A_2}{A_3}\), …, \(S{A_n}{A_1}\). Hình gồm đa giác \({A_1}{A_2}...{A_n}\) và n tam giác \(S{A_1}{A_2}\), \(S{A_2}{A_3}\), …, \(S{A_n}{A_1}\) gọi là hình chóp, kí hiệu \(S.{A_1}{A_2}...{A_n}\).

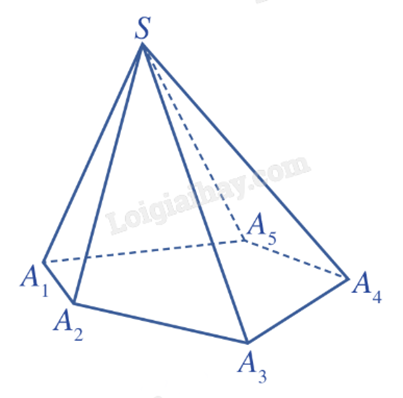
Trong hình chóp \(S.{A_1}{A_2}...{A_n}\), ta có:

- Điểm S gọi là đỉnh;

- Đa giác \({A_1}{A_2}...{A_n}\) gọi là mặt đáy;

- Các cạnh của mặt đáy gọi là cạnh đáy;

- Các đoạn thẳng \(S{A_1}\), \(S{A_2}\), …, \(S{A_n}\) gọi là các cạnh bên;

- Các tam giác \(S{A_1}{A_2}\), \(S{A_2}{A_3}\), …, \(S{A_n}{A_1}\) gọi là các mặt bên.

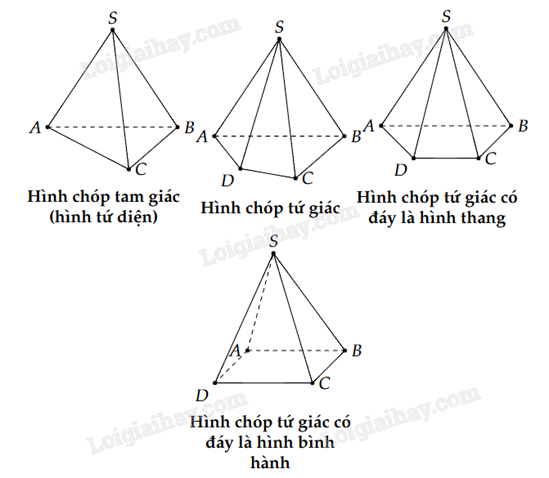
Nếu đáy của hình chóp là một tam giác, tứ giác, ngũ giác,… thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,…

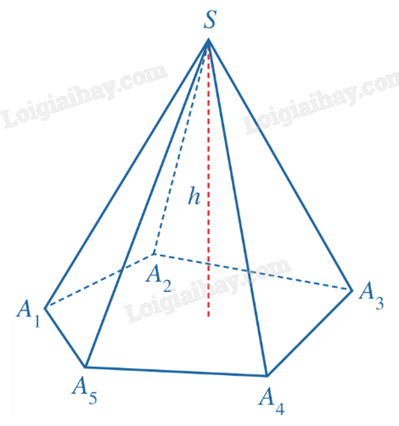
Sử dụng công thức: \(V = \frac{1}{3}S.h\).

Trong đó:

- V: thể tích khối chóp.

- S: diện tích đáy khối chóp.

- h: chiều cao khối chóp.

Ví dụ minh hoạ:

1) Tính thể tích của khối chóp S.ABCD. Biết đáy ABCD là hình vuông cạnh a, \(SA \bot (ABCD)\), góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng \({60^o}\).

Giải:

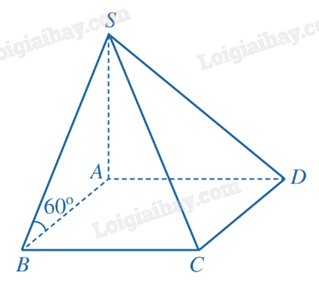
Do \(SA \bot (ABCD)\) và \(BA \subset (ABCD)\) nên \(SA \bot AB\), suy ra \(SA = AB.\tan \widehat {SBA}\).

Vì \(SA \bot (ABCD)\) nên góc giữa đường thẳng SB và mặt phẳng \((ABCD)\) bằng \(\widehat {SBA}\).

Suy ra \(\widehat {SBA} = {60^o}\).

Từ đó, ta có \(SA = a.\tan {60^o} = a\sqrt 3 \). Mặt khác, do diện tích hình vuông ABCD là \({S_{ABCD}} = {a^2}\) nên thể tích của khối chóp S.ABCD là:

\({V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SA = \frac{1}{3}{a^2}.a\sqrt 3  = \frac{{{a^3}\sqrt 3 }}{3}\).

2) Tính thể tích khối từ diện đều SABC cạnh a.

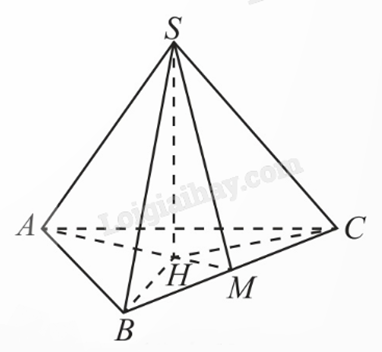
Gọi H là hình chiếu vuông góc của S xuống (ABC). Ta có ba tam giác vuông SHA, SHB, SHC bằng nhau, suy ra HA = HB = HC. Vậy H là tâm của tam giác đều ABC. Ta có:

\(AM = \frac{{a\sqrt 3 }}{2}\), \(AH = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\), \(SH = \sqrt {S{A^2} - A{H^2}}  = \sqrt {{a^2} - \frac{{3{a^2}}}{9}}  = \frac{{a\sqrt 6 }}{3}\).

Khối từ diện đều SABC có thể tích là:

\(V = \frac{1}{3}{S_{ABC}}.SH = \frac{1}{3}\frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 6 }}{3} = \frac{{{a^3}\sqrt 2 }}{{12}}\).