Biến cố hợp là gì? Cách xác định biến cố hợp - Toán 11

Cho A và B là hai biến cố. Biến cố “A hoặc B xảy ra” được gọi là biến cố hợp của A và B, kí hiệu là \(A \cup B\).

Biến cố hợp của A và B là tập con \(A \cup B\) của không gian mẫu \(\Omega \).

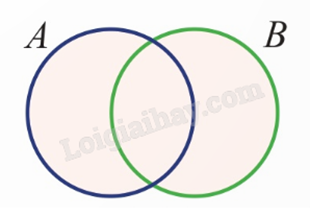
Chú ý: Biến cố \(A \cup B\) xảy ra khi có ít nhất một trong hai biến cố A và B xảy ra. Tập hợp mô tả biến cố \(A \cup B\) là hợp của hai tập hợp mô tả biến cố A và biến cố B.

Sử dụng định nghĩa biến cố hợp.

Ví dụ minh hoạ:

1) Một hộp chứa 5 viên bi xanh và 3 viên bi đỏ có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp. Gọi A là biến cố “Hai viên bi lấy ra đều có màu xanh”, B là biến cố “Hai viên bi lấy ra đều có màu đỏ”.

a) Có bao nhiêu kết quả thuận lợi cho biến cố A? Có bao nhiêu kết quả thuận lợi cho biến cố B?

b) Hãy mô tả bằng lời biến cố \(A \cup B\) và tính số kết quả thuận lợi cho biến cố \(A \cup B\).

Giải:

a) Số kết quả thuận lợi cho biến cố A là \(C_5^2 = 10\).

Số kết quả thuận lợi cho biến cố B là \(C_3^2 = 3\).

b) \(A \cup B\) là biến cố “Hai viên bi lấy ra có cùng màu”. Số kết quả thuận lợi cho biến cố \(A \cup B\) là \(C_5^2 + C_3^2 = 13\).

2) Một hộp đựng 15 tấm thẻ cùng loại được đánh số từ 1 đến 15. Rút ngẫu nhiên một tấm thẻ trong hộp. Gọi E là biến cố “Số ghi trên tấm thẻ là số lẻ”; F là biến cố “Số ghi trên tấm thẻ là số nguyên tố”.

a) Mô tả không gian mẫu.

b) Nêu nội dung của biến cố hợp \(G = E \cup F\). Hỏi G là tập con nào của không gian mẫu?

Giải:

a) Không gian mẫu \(\Omega  = \{ 1;2;3;4;5;6;7;8;9;10;11;12;13;14;15\} \).

b) Biến cố G là “Số ghi trên tấm thẻ là số lẻ hoặc số nguyên tố”.

Ta có \(E = \{ 1;3;5;7;9;11;13;15\} \); \(F = \{ 2;3;5;7;11;13\} \).

Vậy \(G = E \cup F = \{ 1;2;3;5;7;9;11;13;15\} \).