Biến cố giao là gì? Cách xác định biến cố giao - Toán 11

Cho A và B là hai biến cố. Biến cố “Cả A và B đều xảy ra” được gọi là biến cố giao của A và B, kí hiệu là AB.

Biến cố giao của A và B là tập con \(A \cap B\) của không gian mẫu \(\Omega \).

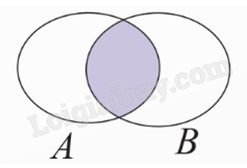
Chú ý: Tập hợp mô tả biến cố AB là giao của hai tập hợp mô tả biến cố A và biến cố B. Biến cố AB xảy ra khi và chỉ khi cả hai biến cố A và B xảy ra.

Sử dụng định nghĩa biến cố giao.

Ví dụ minh hoạ:

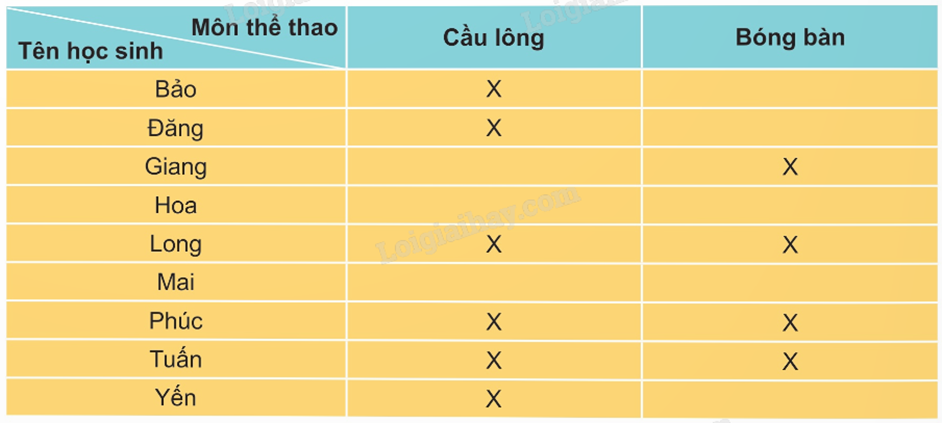
1) Một lớp trong tổ 11C có 9 học sinh. Phỏng vấn 9 bạn này với câu hỏi: “Bạn có biết chơi môn thể thao nào trong hai môn này không?”. Nếu biết thì đánh dấu X vào ô ghi tên môn thể thao đó, không biết thì để trống. Kết quả thu được như sau:

Chọn ngẫu nhiên một học sinh trong tổ. Xét các biến cố sau:

U: “Học sinh được chọn biết chơi cầu lông”;

V: “Học sinh được chọn biết chơi bóng bàn”.

a) Mô tả không gian mẫu.

b) Nội dung của biến cố giao T = UV là gì? Mỗi biến cố U, V, T là tập con nào của không gian mẫu?

Giải:

a) Không gian mẫu \(\Omega  = \) {Bảo; Đăng; Giang; Hoa; Long; Mai; Phúc; Tuấn; Yến}.

b) T là biến cố “Học sinh được chọn biết chơi cả cầu lông và bóng bàn”.

Ta có: U = {Bảo; Đăng; Long; Phúc; Tuấn; Yến}, V = {Giang; Long; Phúc; Tuấn}.

Vậy \(T = U \cap V = \) {Long; Phúc; Tuấn}.

2) Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, ..., 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”. Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, \(A \cap B\).

Giải:

Ta có A = {3; 6; 9; 12; 15; ...; 48; 51}; B = {4; 8; 12; 16; 20; ...; 48; 52};

\(A \cap B\) = {12; 24; 36; 48}.