Công thức tính góc trong không gian - Từ điển Toán 12 
1. Công thức tính góc giữa đường thẳng và mặt phẳng
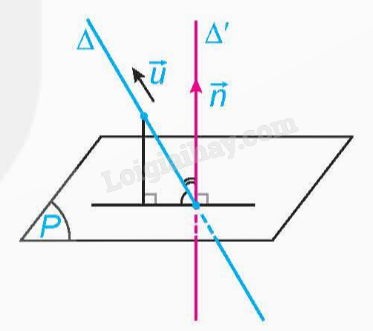
Trong không gian Oxyz, cho đường thẳng d có vecto chỉ phương \(\overrightarrow a = ({a_1};{a_2};{a_3})\) và mặt phẳng \((\alpha )\) có vecto pháp tuyến \(\overrightarrow n = (A;B;C)\). Kí hiệu \(\left( {d,(\alpha )} \right)\) là góc giữa đường thẳng d và mặt phẳng \((\alpha )\). Khi đó:
\(\sin (d,(\alpha )) = \frac{{\left| {\overrightarrow n .\overrightarrow a } \right|}}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow a } \right|}} = \frac{{\left| {{a_1}A + {a_2}B + {a_3}C} \right|}}{{\sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} .\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Lưu ý:
+ \({0^o} \le (d,(\alpha )) \le {90^o}\).
+ Nếu \(d//(\alpha )\) hoặc \(d \subset (\alpha )\) thì \((d,(\alpha )) = {0^o}\).
+ \(d \bot (\alpha ) \Leftrightarrow (d,(\alpha )) = {90^o}\).
2. Ví dụ minh hoạ
Trong không gian Oxyz, tính góc giữa đường thẳng d: \(\frac{x}{{ - 1}} = \frac{y}{2} = \frac{{z - 1}}{{ - 1}}\) và mặt phẳng \((\alpha )\): \(x + y - 2z + 1 = 0\).
Giải:
Đường thẳng d có vectơ chỉ phương \(\overrightarrow a = ( - 1;2; - 1)\), mặt phẳng \((\alpha )\) có vectơ pháp tuyến \(\overrightarrow n = \left( {1;1; - 2} \right)\).
Ta có: \(\sin (d,(\alpha )) = \frac{{\left| {\overrightarrow n .\overrightarrow a } \right|}}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow a } \right|}} = \frac{{\left| {( - 1).1 + 2.1( - 1).( - 2)} \right|}}{{\sqrt {{{( - 1)}^2} + {2^2} + {{( - 1)}^2}} .\sqrt {{1^2} + {1^2} + {{( - 2)}^2}} }} = \frac{1}{2}\).
Vậy \((d,(\alpha )) = {30^o}\).
