Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\); tứ giác \(ABCD\) là hình thang vuông với cạnh đáy \(AD,BC\); \(AD = 3BC = 3a,\,\,AB = a,SA = a\sqrt 3 \). Điểm \(I\) thỏa mãn \(\overrightarrow {AD} = 3\overrightarrow {AI} \); \(M\) là trung điểm \(SD\), \(H\) là giao điểm của \(AM\) và \(SI\). Gọi \(E\), \(F\) lần lượt là hình chiếu của \(A\) lên \(SB\), \(SC.\) Tính thể tích \(V\) của khối nón có đáy là đường tròn ngoại tiếp tam giác \(EFH\) và đỉnh thuộc mặt phẳng\(\left( {ABCD} \right)\).
-
A.
\(V = \dfrac{{\pi {a^3}}}{{2\sqrt 5 }}\).
-
B.
\(V = \dfrac{{\pi {a^3}}}{{\sqrt 5 }}\).
-
C.
\(V = \dfrac{{\pi {a^3}}}{{10\sqrt 5 }}\).
-
D.
\(V = \dfrac{{\pi {a^3}}}{{5\sqrt 5 }}\).
- Chứng minh tứ giác \(AEFH\) nội tiếp, từ đó tìm tâm đường tròn ngoại tiếp tam giác \(EHF\).
- Tìm đỉnh hình nón và tính chiều cao, bán kính đáy rồi suy ra thể tích.
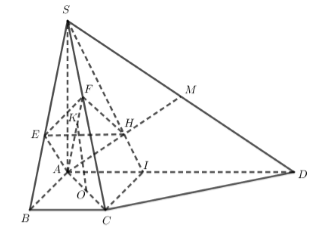
Xét tam giác \(SAD\) vuông tại \(A\) có \(SA = a\sqrt 3 ,AD = 3a \Rightarrow \widehat {SDA} = {30^0}\) \( \Rightarrow \widehat {MAI} = {30^0}\).
Lại có tam giác \(SAI\) vuông tại \(A\) có \(SA = a\sqrt 3 ,AI = a \Rightarrow \widehat {SIA} = {60^0}\) nên tam giác \(AHI\) có \(\widehat H = {90^0}\) hay \(AH \bot SI\)
Mà \(AH \bot IC\) do \(IC//BA \bot \left( {SAD} \right)\) nên \(AH \bot \left( {SIC} \right)\) \( \Rightarrow AH \bot SC\).
Ngoài ra, \(AE \bot SB,AE \bot BC\left( {BC \bot \left( {SAB} \right)} \right) \Rightarrow AE \bot \left( {SBC} \right) \Rightarrow AE \bot SC\).
Mà \(AF \bot SC\) nên \(SC \bot \left( {AEFH} \right)\) và \(AEFH\) là tứ giác có \(\widehat E = \widehat H = {90^0}\) nên nội tiếp đường tròn tâm \(K\) là trung điểm \(AF\) đường kính \(AF\).
Gọi \(O\) là trung điểm \(AC\) thì \(OK//SC\), mà \(SC \bot \left( {AEFH} \right)\) nên \(OK \bot \left( {AEFH} \right)\) hay \(O\) chính là đỉnh hình nón và đường tròn đáy là đường tròn đường kính \(AF\).
Ta tính \(AF,OK\).
Xét tam giác \(SAC\) vuông tại \(A\) đường cao \(AF\) nên \(AF = \dfrac{{SA.AC}}{{SC}} = \dfrac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{a\sqrt 6 }}{{\sqrt 5 }}\).; \(OK = \dfrac{1}{2}CF = \dfrac{1}{2}.\dfrac{{C{A^2}}}{{CS}} = \dfrac{a}{{\sqrt 5 }}\).
Vậy thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi .\dfrac{a}{{\sqrt 5 }}.{\left( {\dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{{\sqrt 5 }}} \right)^2} = \dfrac{{\pi {a^3}}}{{10\sqrt 5 }}\).
Đáp án : C
Các bài tập cùng chuyên đề
Công thức tính diện tích xung quanh hình nón có bán kính đáy \(r\) và độ dài đường sinh \(l\) là
Diện tích xung quanh hình nón có bán kính đáy \(r = 3cm\) và độ dài đường sinh \(4cm\) là:
Cho hình nón bán kính đáy \(r\) và diện tích xung quanh \({S_{xq}}\). Độ dài đường sinh \(l\) của hình nón là:
Gọi \(r,l,h\) lần lượt là bán kính đáy, độ dài đường sinh và chiều cao của hình nón. Chọn mệnh đề đúng:
Công thức tính diện tích toàn phần hình nón có bán kính đáy \(r\), độ dài đường cao \(h\) và độ dài đường sinh \(l\) là:
Cho hình nón có các kích thước \(r = 1cm;l = 2cm\) với \(r,l\) lần lượt là bán kính đáy và độ dài đường sinh hình nón. Diện tích toàn phần hình nón là:
Cho hình nón có các kích thước \(r = 1;h = 2\) với \(r,h\) lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:
Công thức tính thể tích khối nón có bán kính đáy \(r\), độ dài đường sinh \(l\) và chiều cao \(h\) là:
Thể tích khối nón có bán kính đáy \(r\), độ dài đường sinh \(l\) là:
Thể tích khối nón có bán kính đáy \(r = 2cm\) và \(h = 3cm\) là:
Công thức tính thể tích khối nón biết diện tích đáy \({S_d}\) và đường sinh \(l\) là:
Cho tam giác $ABO$ vuông tại $O$, có góc \(\widehat {BAO} = {30^0},AB = a\) . Quay tam giác $ABO$ quanh trục $AO$ ta được một hình nón có diện tích xung quanh bằng:
Một hình nón tròn xoay có đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng $9\pi $. Khi đó chiều cao $h$ của hình nón bằng:
Hình nón có thiết diện qua trục là tam giác đều cạnh \(a = 3\). Tính độ dài đường cao của hình nón.
Một hình nón có bán kính đáy bằng $1$, chiều cao nón bằng $2$. Khi đó góc ở đỉnh của nón là $2\varphi $ thỏa mãn
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là $a$ và $2a$ sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Bán kính đáy của hình nón đã cho là:
Cho hình nón có diện tích xung quanh bằng \(3\pi {a^2}\) và bán kính đáy bằng \(a\). Tính độ dài đường sinh \(l\) của hình nón đã cho.
Cho mặt cầu tâm \(O\) bán kính \(R\). Xét mặt phẳng \(\left( P \right)\) thay đổi cắt mặt cầu theo giao tuyến là đường tròn \(\left( C \right)\). Hình nón \(N\) có đỉnh \(S\) nằm trên mặt cầu, có đáy là đường tròn \(\left( C \right)\) và có chiều cao \(h\left( {h > R} \right)\). Tìm \(h\) để thể tích khối nón được tạo nên bởi \(\left( N \right)\) có giá trị lớn nhất.
Cho hình nón đỉnh $S$, tâm đáy là $O$, góc ở đỉnh là ${135^0}$. Trên đường tròn đáy lấy điểm $A$ cố định và điểm $M$ di động. Tìm số vị trí $M$ để diện tích $SAM$ đạt giá trị lớn nhất
Một que kem ốc quế gồm hai phần: phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón có bán kính bằng nhau; biết rằng nếu kem tan chảy hết thì sẽ làm đầy phần ốc quế. Biết thể tích phần kem sau khi tan chảy chỉ bằng $75\% $ thể tích kem đóng băng ban đầu. Gọi $h$ và $r$ lần lượt là chiều cao và bán kính của phần ốc quế. Tính tỉ số \(\dfrac{h}{r}\).
