Cho tam giác ABC có \(AB = 9cm,AC = 12cm,BC = 15cm.\)
a) Chứng minh tam giác ABC vuông tại A.
b) Trên tia đối của tia AB, lấy điểm D sao cho \(AD = 5cm.\) Tính độ dài CD.
a) Sử dụng định lí Pythagore đảo
b) Sử dụng định lí Pythagore để tính độ dài CD.
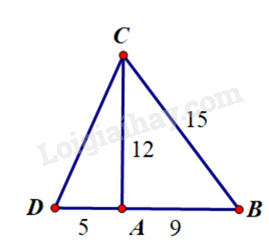
a) Ta có \(A{B^2} + A{C^2} = {9^2} + {12^2} = 225 = {15^2} = B{C^2}\)
Tam giác ABC vuông tại A (định lí Pythagore đảo).
b) Xét tam giác ABC vuông tại A suy ra \(AC \bot BD \Rightarrow \widehat {DAC} = {90^0}\)
Xét tam giác ADC vuông tại A có:
\(A{D^2} + A{C^2} = D{C^2}\)(định lí Pythagore)
\( \Rightarrow DC = \sqrt {{{12}^2} + {5^2}} = 13cm.\)

Các bài tập cùng chuyên đề
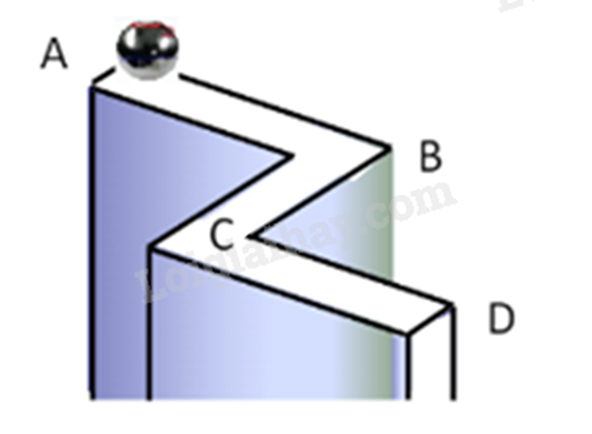
Một viên bi lăn theo đoạn đường từ A đến D như hình vẽ \((AB \bot BC,BC \bot CD)\). Hãy tính khoảng cách AD. Biết rằng AB = 10m, BC = 12m, CD = 6m.
Cho hình chữ nhật \(ABCD\), kẻ \(AH \bot BD\) tại \(H\).
a) Chứng minh \(\Delta ADH\) đồng dạng với \(\Delta BDA\).
b) Chứng minh \(\Delta AHD\) đồng dạng với \(\Delta BHA\) và \(A{H^2} = DH.BH\)
c) Tính \(AD, AB\) biết \(DH = 9 cm, BH = 16 cm\).
d) Gọi \(K, M, N\) lần lượt là trung điểm của \(AH, BH, CD\). Chứng minh rằng tứ giác \(MNDK\) là hình bình hành và \(\widehat {AMN} = {90^o}\).
Cho tam giác \(ABC\), đường cao \(AH\). Biết \(AC = 15\,cm\), \(AH = 12\,cm\), \(BH = 9\,cm\). Kết luận nào sau đây là đúng?
-
A.
\(\Delta ABC\) vuông;
-
B.
\(\Delta ABC\) cân;
-
C.
\(\Delta ABC\) tù;
-
D.
\(\Delta ABC\) vuông cân.
Cho tam giác \(ABC\) vuông tại \(A\), có \(AB = 6\, cm\), \(AC = 8\, cm\). \(D\) là một điểm sao cho \(BD = 16\, cm\), \(CD = 24\, cm\). Khẳng định nào sau đây là đúng?
-
A.
Ba điểm \(B,\, C,\, D\) thẳng hàng;
-
B.
Tam giác \(BCD\) là tam giác vuông;
-
C.
Tam giác \(BCD\) không thể là tam giác vuông;
-
D.
Tam giác \(BCD\) là tam giác cân.
Cho tam giác \(ABH\) vuông tại \(H\) có \(AB = 20\, cm\), \(BH = 12\, cm\). Trên tia đối của tia \(HB\) lấy điểm \(C\) sao cho \(AC = \frac{5}{3}AH\). Chọn đáp án đúng.
-
A.
\(\widehat {BAC} = {90^o}\);
-
B.
\(\widehat {BAC} = {120^o}\);
-
C.
\(\widehat {BAC} = {45^o}\);
-
D.
\(\widehat {BAC} = {60^o}\).
Cho tam giác \(ABC\) có độ dài các cạnh \(AB\), \(BC\), \(CA\) lần lượt là \(4\,cm\), \(3\,cm\), \(5\,cm\). Trên tia đối của tia \(BA\) lấy điểm \(M\) sao cho \(BM = 2\,cm\), tại \(M\) kẻ đường thẳng vuông góc với \(AB\) cắt \(AC\) tại \(H\). Chọn khẳng định đúng.
-
A.
\(BC\) vuông góc \(MH\);
-
B.
\(BC\) trùng với \(MH\);
-
C.
\(BC\) song song với \(MH\);
-
D.
Tất cả đều sai.
Cho tam giác \(ABC\) có \(AB = 6\, cm\), \(AC = 8\, cm\), \(BC = 10\, cm\) và đường cao \(AH\). Tính độ dài \(AH\).
-
A.
\(AH = 2,4\, cm\);
-
B.
\(AH = 3,6\, cm\);
-
C.
\(AH = 4,8\, cm\);
-
D.
\(AH = 5,4\, cm\).
Cho tam giác ABC vuông tại đỉnh A. Gọi AD là đường cao của tam giác. Biết rằng \(BD = 2cm,CD = 8cm.\) Hãy tính độ dài các cạnh AB, AC và chiều cao AD của tam giác ABC.
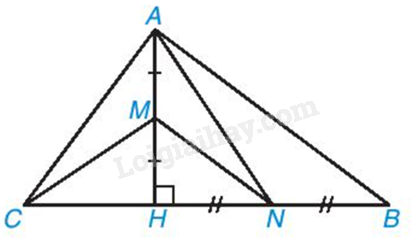
Cho tam giác ABC có đường cao AH. Biết AH = 12cm, CH = 9cm, BH = 16cm. Lấy M, N lần lượt là trung điểm của AH, BH
a) Chứng minh rằng ABC là tam giác vuông tại A
b) Chứng minh rằng MN ⊥ AC và CM ⊥ AN
c) Tính diện tích tam giác AMN
Cho \(\Delta ABC\) vuông tại A có \(AB = 12cm,AC = 16cm\). Đường cao AH. Độ dài đoạn thẳng AH là …cm. (viết dưới dạng số thập phân)







Danh sách bình luận