Bài 1 trang 41 SGK Đại số 10
Vẽ đồ thị hàm số.
Video hướng dẫn giải
Vẽ đồ thị hàm số:
LG a
\(y = 2x - 3\);
Phương pháp giải:
Cho y=0 suy ra \(- \frac{b}{a}\) ta được điểm \(A\left( { - \frac{b}{a};0} \right)\)
Cho x=0 suy ra y=b ta được điểm \(B\left( {0;b} \right)\).
Nối hai điểm A, B được đồ thị hàm số.
Lời giải chi tiết:
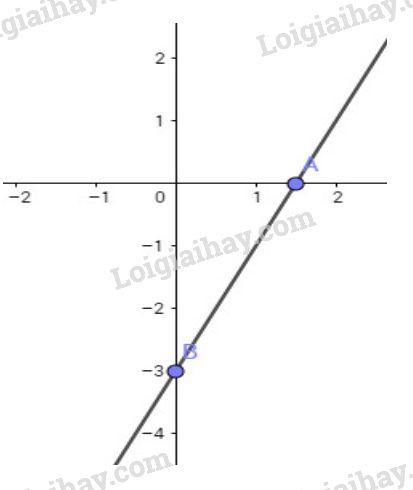
Cho \(y = 0\) ta có: \(0 = 2x - 3 \Leftrightarrow 2x = 3 \Leftrightarrow x = \frac{3}{2}\) nên điểm \(A\left( {\frac{3}{2};0} \right)\) thuộc ĐTHS
Cho \(x = 0\) ta có: \(y = 2.0 - 3 = - 3\) nên điểm \(B\left( {0; - 3} \right)\) thuộc ĐTHS.
Vẽ đồ thị:
LG b
\(y = \sqrt 2\);
Phương pháp giải:
Đồ thị của hàm số y = b là một đường thẳng song song hoặc trùng với trục hoành và đi qua điểm (0;b).
Lời giải chi tiết:
Đồ thị hàm số \(y = \sqrt 2\) là đường thẳng song song với trục hoành và đi qua điểm \(A(0; \sqrt 2)\)

LG c
\(y=-\frac{3x}{2}+7;\)
Phương pháp giải:
Lần lượt cho x=2, x=4 tìm điểm đi qua của ĐTHS.
Nối hai điểm A, B được đồ thị hàm số.
Lời giải chi tiết:
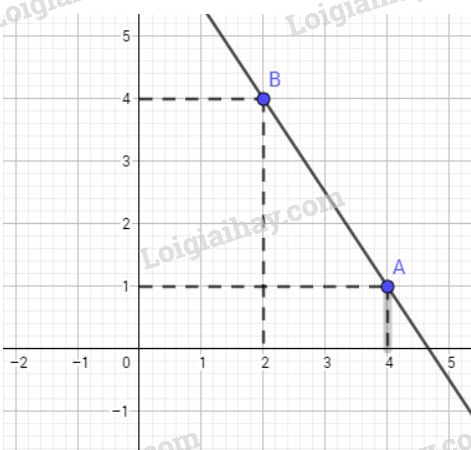
Cho \(x = 4\) ta có \(y = - \frac{{3.4}}{2} + 7 = 1\) nên điểm \(A\left( {4;1} \right)\) thuộc ĐTHS.
Cho \(x = 2\) ta có \(y = \frac{{ - 3.2}}{2} + 7 = 4\) nên điểm \(B\left( {2;4} \right)\) thuộc ĐTHS.
Vẽ đồ thị:
Chú ý:
Các em cũng có thể vẫn cho x=0, y=0 tìm điểm như thông thường nhưng bởi vì giao điểm của đồ thị với trục tung \(P(0; 7)\), với trục hoành \(Q=(\frac{14}{3};0)\) có tọa độ tương đối lớn nên ta có thể chọn các điểm thuộc đồ thị có tọa độ nhỏ hơn cho dễ vẽ. Chẳng hạn \(A(4; 1), B(2; 4)\) như trên.
LG d
\(y = |x|-1\).
Phương pháp giải:
Phá dấu giá trị tuyệt đối dựa vào điều kiện của x.
Vẽ đồ thị từng hàm số trong mỗi khoảng xác định.
Từ đó suy ra đồ thị hàm số đã cho.
Lời giải chi tiết:
Vì \(\left| x \right| = \left\{ \begin{array}{l}
x\,\text{nếu}\,x \ge 0\\
- x\,\text{nếu}\,x < 0
\end{array} \right.\)
nên \(y = |x| - 1 = \left\{ \matrix{
x - 1,x \ge 0 \hfill \cr
- x - 1,x < 0 \hfill \cr} \right.\)
Do đó đồ thị hàm số cần vẽ là hợp của hai nửa đường thẳng:
+) nửa đường thẳng \(y=x-1\) với \(x\ge 0\)
+) nửa đường thẳng \(y=-x-1\) với \(x<0\)

Chú ý:
Cách vẽ hình như sau:
* Vẽ đường thẳng y=x-1.
Cho x=0 thì y=-1 ta được điểm (0;-1).
Cho y=0 thì x=1 ta được điểm (1;0).
Nối hai điểm này kéo dài được đường thẳng y=x-1.
Do \(x \ge 0\) nên ta chỉ lấy nửa đường thẳng bên phải trục tung và xóa nửa còn lại đi.
* Vẽ đường thẳng y=-x-1.
Cho x=0 thì y=-1 ta được điểm (0;-1).
Cho y=0 thì x=-1 ta được điểm (-1;0).
Nối hai điểm này kéo dài được đường thẳng y=-x-1.
Do \(x < 0\) nên ta chỉ lấy nửa đường thẳng bên trái trục tung và xóa nửa còn lại đi.
* Hợp hai nửa đường thẳng còn lại trên hình ta được đồ thị cần tìm.
Loigiaihay.com













Danh sách bình luận