Khái niệm đồ thị, đỉnh, cạnh trong lí thuyết đồ thị - Toán 11

Một đồ thị là một tập hợp gồm hữu hạn các điểm (gọi là đỉnh của đồ thị) cùng với tập hợp các đoạn đường cong hay thẳng (gọi là cạnh của đồ thị) có đầu mút tại các đỉnh của đồ thị.

Chú ý: Các cạnh của đồ thị thẳng hay cong, dài hay ngắn, các đỉnh ở vị trí nào đều không quan trọng.

Giả sử có đồ thị G:

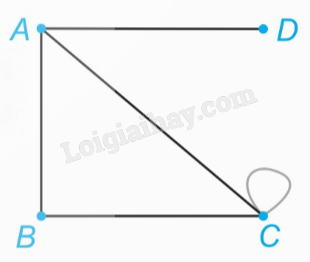
- Tập hợp đỉnh V(G) = {A, B, C, D}.

- Tập hợp cạnh E(G) = {AB, AC, AD, BC, CC}.

- Hai đỉnh kề nhau nếu chúng là hai đầu mút của một cạnh, ví dụ A – B.

- Một đỉnh không kề với đỉnh nào (kể cả chính nó) gọi là đỉnh cô lập.

- Cạnh có hai đầu mút trùng nhau gọi là khuyên, ví dụ CC.

1) Cho đồ thị G:

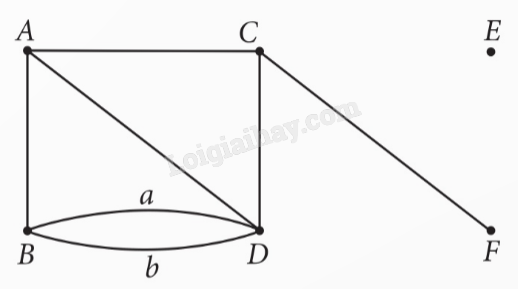
- Các đỉnh của G là: A, B, C, D, E và F. Đồ thị có 6 đỉnh.

- Các cạnh của G là: AB, AC, AD, a, b, CD và CF. Đồ thị có 7 đỉnh.

- Các đỉnh kề đỉnh A: B, C, D.

- Đỉnh cô lập: E.

2) Năm người A, B, C, D và E cùng đến dự một bữa tiệc. Biết rằng, trước khi đến dự tiệc, mối quan hệ quen biết (người này quen người kia và ngược lại) giữa những người này như sau:

+ A quen với B, C, D và E;

+ B quen với C và E (không tính với A);

+ C quen với D (không tính với A, B);

+ D quen với E (không tính với A, B, C).

a) Vẽ một đồ thị biểu thị mối quan hệ quen biết giữa năm người này trước khi đến dự tiệc.

b) Biết rằng, tại buổi tiệc, mỗi người đều bắt tay với người đã quen và không bắt tay với người chưa quen. Có tất cả bao nhiêu lần bắt tay giữa năm người trên?

Giải:

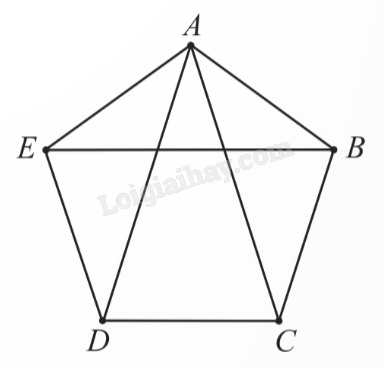
a) Ta vẽ đồ thị G có 5 đỉnh biểu diễn năm người A, B, C, D và E; hai đỉnh được nối bằng một cạnh nếu giữa hai người mà chúng biểu diễn quen nhau.

b) Số lần bắt tay bằng số cạnh của đồ thị G. Ta đếm được đồ thị có 8 cạnh. Vậy, có 8 lần bắt tay giữa năm người A, B, C, D và E.