Bậc của đỉnh. Đỉnh bậc lẻ. Đỉnh bậc chẵn - Toán 11

Giả sử A là đỉnh của một đồ thị. Số cạnh của đồ thị có A là đầu mút gọi là bậc của đỉnh A, kí hiệu d(A).

Đỉnh có bậc là một số chẵn được gọi là đỉnh bậc chẵn, đỉnh có bậc là một số lẻ gọi là đỉnh bậc lẻ.

Đỉnh cô lập có bậc bằng 0.

Trong mọi đồ thị G, tổng tất cả các bậc của các đỉnh là một số chẵn và bằng hai lần tổng tất cả các cạnh của G.

Hệ quả: Số đỉnh bậc lẻ của mọi đồ thị là một số chẵn.

1) Chỉ ra bậc của đỉnh ở mỗi đồ thị.

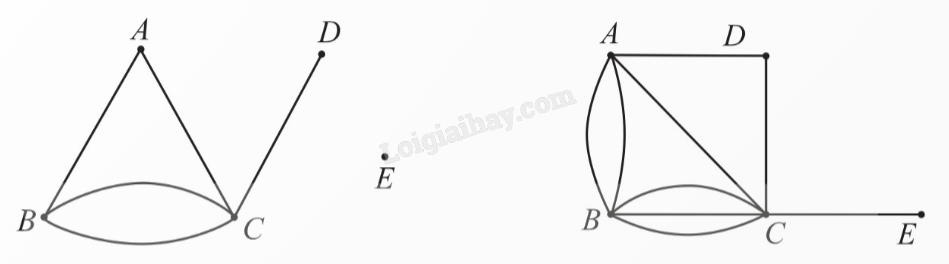
Giải:

Trong đồ thị bên trái, ta có d(A) = 2, d(B) = 3, d(C) = 4, d(E) = 0.

Trong đồ thị bên phải, ta có d(A) = 4, d(B) = 5, d(C) = 6, d(E) = 1.

2) Hãy tìm những đỉnh có bậc lẻ, những đỉnh có bậc chẵn.

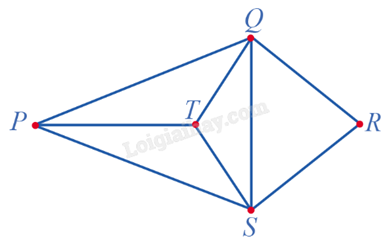
Giải:

Do d(P) = 3, d(Q) = 4, d(R) = 2, d(S) = 4, d(T) = 3 nên P, T là các đỉnh bậc lẻ; Q, R, S là các đỉnh bậc chẵn.

3) Vẽ một đồ thị (nếu có) có 5 đỉnh với bậc của các đỉnh lần lượt là:

a) 2; 3; 3; 3; 3.

b) 1; 2; 3; 4; 5.

Giải:

a)

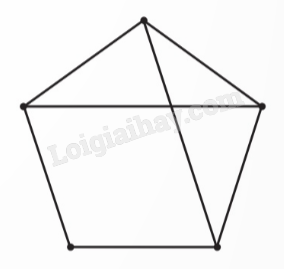
b) Không có, vì tổng bậc các đỉnh 1 + 2 + 3 + 4 + 5 = 15 là số lẻ (theo định lí bắt tay, tổng tất cả các bậc của các đỉnh là một số chẵn).

4) Cho đồ thị G với 14 đỉnh và 25 cạnh. Biết rằng mỗi đỉnh của đồ thị G đều có bậc 3 hoặc bậc 5. Hỏi G có bao nhiêu đỉnh bậc 3?

Giải:

Gọi x là số đỉnh bậc 3 của G. Khi đó số đỉnh bậc 5 của G là 14 – x. Tổng tất cả các bậc của đỉnh là 3x + 5(14 – x).

Vì đồ thì có 25 cạnh nên ta có: \(3x + 5 + (14 - x) = 2.25 \Leftrightarrow x = 10\).

Vậy đồ thị G có 10 đỉnh bậc 3.