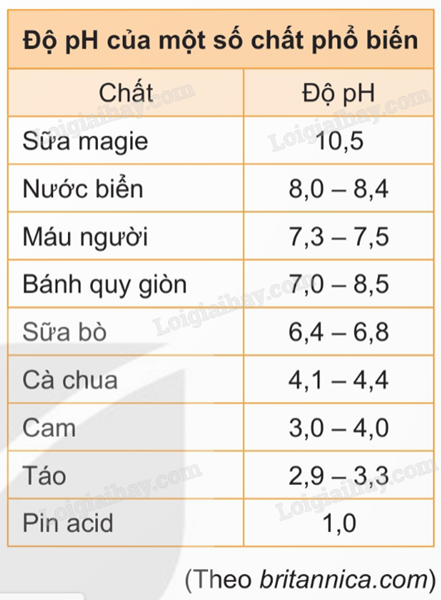
Cách giải bài toán về độ pH ứng dụng logarit - Toán 11

\(pH =  - \log [{H^ + }]\)

1) Sử dụng máy tính cầm tay để tính độ pH trong mỗi trường hợp sau (làm tròn kết quả đến hàng phần mười):

a) Bia có \([{H^ + }] = 0,00008\);

b) Rượu có \([{H^ + }] = 0,0004\).

(Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2021).

Giải:

a) \(pH =  - \log [{H^ + }] =  - \log (0,00008) \approx 4,1\).

b) \(pH =  - \log [{H^ + }] =  - \log (0,0004) \approx 3,4\).

2) Độ pH của một dung dịch hoá học được tính theo công thức \(pH =  - \log [{H^ + }]\), trong đó \([{{\rm{H}}^ + }]\) là nồng độ (tính theo mol/lít) của các ion hydrogen. Giá trị pH nằm trong khoảng từ 0 đến 14. Nếu pH < 7 thì dung dịch có tính acid, nếu pH > 7 thì dung dịch có tính base, còn nếu pH = 7 thì dung dịch là trung tính.

a) Tính độ pH của dung dịch có nồng độ ion hydrogen bằng 0,01 mol/lít.

b) Xác định nồng độ ion hydrogen của một dung dịch có độ pH bằng 7,4.

Giải:

a) Khi \([{{\rm{H}}^ + }] = 0,01\), ta có: 

\({\rm{pH}} =  - \log 0,01 =  - \log {10^{ - 2}} = 2.\)

b) Nồng độ ion hydrogen trong dung dịch đó là \([{{\rm{H}}^ + }] = {10^{ - 7,4}}\).

3) Trong hoá học, độ pH của một dung dịch được tính theo công thức \({\rm{pH}} =  - \log [{{\rm{H}}^ + }]\), trong đó \([{{\rm{H}}^ + }]\) là nồng độ \({{\rm{H}}^ + }\) (ion hydrogen) tính bằng mol/L. Các dung dịch có pH bé hơn 7 thì có tính acid, có pH lớn hơn 7 thì có tính kiềm, có pH bằng 7 thì trung tính.

a) Tính độ pH của dung dịch có nồng độ \({{\rm{H}}^ + }\) là 0,0001 mol/L. Dung dịch này có tính acid, kiềm hay trung tính?

b) Dung dịch A có nồng độ \({{\rm{H}}^ + }\) gấp đôi nồng độ \({{\rm{H}}^ + }\) của dung dịch B. 

Độ pH của dung dịch nào lớn hơn và lớn hơn bao nhiêu? Làm tròn kết quả đến hàng phần nghìn.

Giải:

a) \({\rm{pH}} =  - \log 0,0001 =  - \log {10^{ - 4}} = 4\log 10 = 4\). 

Do \(4 < 7\) nên dung dịch có tính acid.

b) Kí hiệu \({\rm{p}}{{\rm{H}}_A}\), \({\rm{p}}{{\rm{H}}_B}\) lần lượt là độ pH của hai dung dịch A và B; \({[{{\rm{H}}^ + }]_A}\), \({[{{\rm{H}}^ + }]_B}\) lần lượt là nồng độ của hai dung dịch A và B. Ta có:

\({\rm{p}}{{\rm{H}}_A} =  - \log {[{{\rm{H}}^ + }]_A} =  - \log (2{[{{\rm{H}}^ + }]_B}) =  - \log 2 - \log {[{{\rm{H}}^ + }]_B} =  - \log 2 + {\rm{p}}{{\rm{H}}_B}\). 

Suy ra \({\rm{p}}{{\rm{H}}_B} - {\rm{p}}{{\rm{H}}_A} = \log 2 \approx 0,301\). 

Vậy dung dịch B có độ pH lớn hơn và lớn hơn khoảng 0,301.