Hàm số logarit là gì? Tính chất, đồ thị của hàm số logarit - Toán 11

Cho số thực a (a > 0, \(a \ne 1\)). Hàm số \(y = {\log _a}x\) được gọi là hàm số logarit cơ số a.

Hàm số mũ \(y = {\log _a}x\) (a > 0, \(a \ne 1\)):

- Tập xác định: \(\left( {0; + \infty } \right)\).

- Tập giá trị: \(\mathbb{R}\).

- Liên tục trên \(\left( {0; + \infty } \right)\).

- Sự biến thiên:

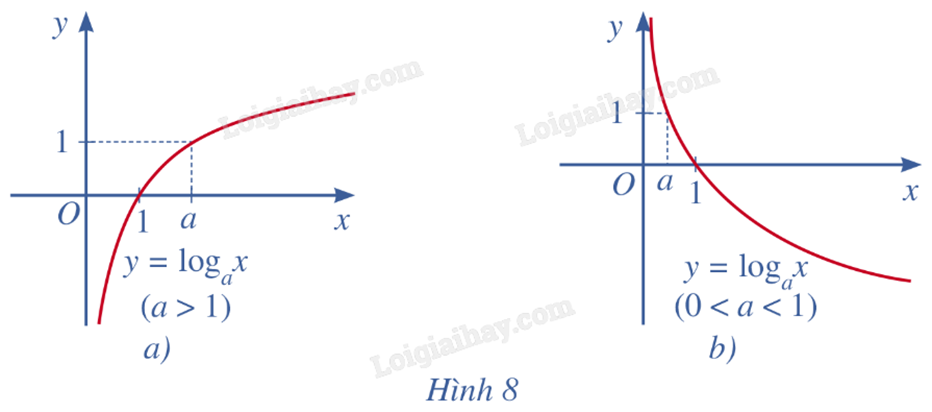
+ Nếu a > 1 thì hàm số đồng biến trên \(\left( {0; + \infty } \right)\) và \(\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } {\log _a}x =  + \infty \); \(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} {\log _a}x =  - \infty \).

+ Nếu 0 < a < 1 thì hàm số nghịch biến trên \(\left( {0; + \infty } \right)\) và \(\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } {\log _a}x =  - \infty \); \(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} {\log _a}x =  + \infty \).

- Đồ thị:

+ Cắt trục hoành tại điểm (1;0), đi qua điểm (a;1).

+ Nằm bên phải trục tung.

Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {\log _3}x\).

Giải:

Vì hàm số \(y = {\log _3}x\) có cơ số 3 > 1 nên ta có bảng biến thiên như sau:

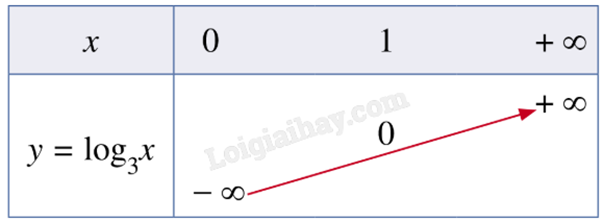
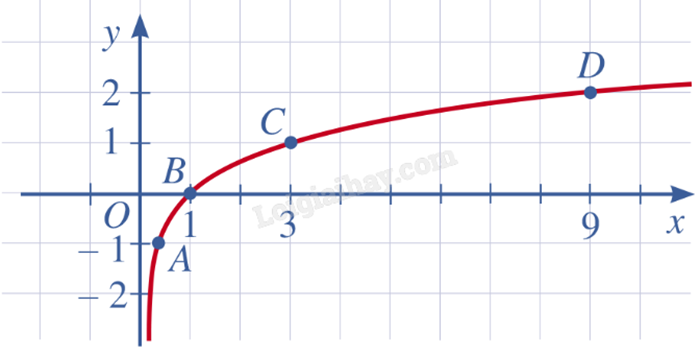
Đồ thị của hàm số \(y = {\log _3}x\) là một đường cong liền nét đi qua các điểm \(A\left( {\frac{1}{3}; - 1} \right)\), \(B\left( {1;0} \right)\), \(C\left( {3;1} \right)\), \(D\left( {9;2} \right)\).