Hình chóp. Hình chóp đều. Hình chóp cụt đều - Toán 11

Trong mặt phẳng (P), cho đa giác \({A_1}{A_2}...{A_n}\) \(\left( {n \ge 3} \right)\). Lấy điểm S nằm ngoài (P). Nối S với các đỉnh \({A_1}\), \({A_2}\), …, \({A_n}\), ta được n tam giác: \(S{A_1}{A_2}\), \(S{A_2}{A_3}\), …, \(S{A_n}{A_1}\). Hình gồm đa giác \({A_1}{A_2}...{A_n}\) và n tam giác \(S{A_1}{A_2}\), \(S{A_2}{A_3}\), …, \(S{A_n}{A_1}\) gọi là hình chóp, kí hiệu \(S.{A_1}{A_2}...{A_n}\).

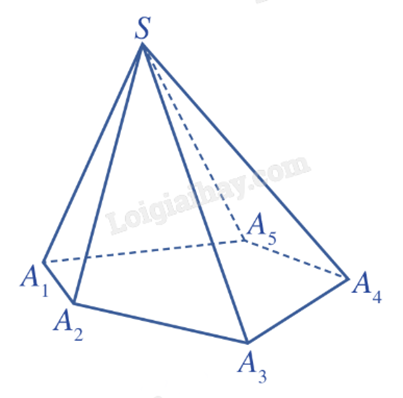
Trong hình chóp \(S.{A_1}{A_2}...{A_n}\), ta có:

- Điểm S gọi là đỉnh;

- Đa giác \({A_1}{A_2}...{A_n}\) gọi là mặt đáy;

- Các cạnh của mặt đáy gọi là cạnh đáy;

- Các đoạn thẳng \(S{A_1}\), \(S{A_2}\), …, \(S{A_n}\) gọi là các cạnh bên;

- Các tam giác \(S{A_1}{A_2}\), \(S{A_2}{A_3}\), …, \(S{A_n}{A_1}\) gọi là các mặt bên.

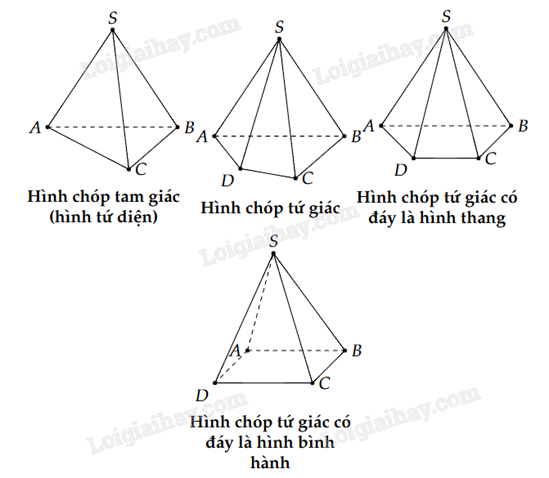
Nếu đáy của hình chóp là một tam giác, tứ giác, ngũ giác,… thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,…

Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau.

Chú ý:

- Khi đáy của hình chóp đều lần lượt là tam giác đều, hình vuông, ngũ giác đều, lục giác đều, ta gọi hình chóp đều đó là hình chóp tam giác đều, hình chóp tứ giác đều, hình chóp ngũ giác đều, hình chóp lục giác đều.

- Hình chóp tam giác đều có cạnh bên bằng cạnh đáy là tứ diện đều.

* Chân đường cao của hình chóp đều là tâm đường tròn ngoại tiếp của đáy.

Cho hình chóp đều \(S.{A_1}{A_2}...{A_n}\). Mặt phẳng (P) song song với đáy của hình chóp và cắt các cạnh \(S{A_1}\), \(S{A_2}\), …, \(S{A_n}\) lần lượt tại \({B_1}\), \({B_2}\), …, \({B_n}\).

Phần của hình chóp đã cho giới hạn bởi hai mặt phẳng (P) và \(\left( {{A_1}{A_2}...{A_n}} \right)\) được gọi là hình chóp cụt đều \({A_1}{A_2}...{A_n}.{B_1}{B_2}...{B_n}\).

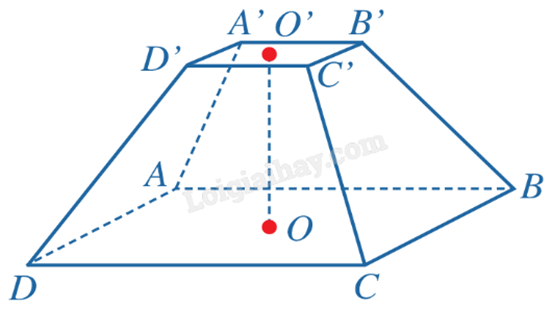
Trong hình chóp đều \({A_1}{A_2}...{A_n}.{B_1}{B_2}...{B_n}\), ta gọi:

- Các đa giác \({A_1}{A_2}...{A_n}\), \({B_1}{B_2}...{B_n}\) lần lượt là đáy lớn, đáy nhỏ;

- Các tứ giác \({A_1}{A_2}{B_2}{B_1}\), \({A_2}{A_3}{B_3}{B_2}\), …, \({A_n}{A_1}{B_1}{B_n}\) là các mặt bên;

- Các đoạn thẳng \({A_1}{B_1}\), \({A_2}{B_2}\), …, \({A_n}{B_n}\) là các cạnh bên;

- Các cạnh của hai đa giác \({A_1}{A_2}...{A_n}\), \({B_1}{B_2}...{B_n}\) là các cạnh đáy;

- Đoạn thẳng nối tâm của hai đa giác \({A_1}{A_2}...{A_n}\), \({B_1}{B_2}...{B_n}\) là đường cao; độ dài đường cao là chiều cao.

Tuỳ theo đáy là tam giác đều, hình vuông, ngũ giác đều,… , ta có hình chóp cụt tam giác đều, hình chóp cụt tứ giác đều, hình chóp cụt ngũ giác đều,…

Nhận xét:

- Hai đáy của hình chóp cụt đều nằm trên hai mặt phẳng song song và có các cạnh tương ứng song song; đồng thời hai đáy đó là các đa giác đều có cùng số cạnh;

- Mỗi mặt bên của hình chóp cụt đều là một hình thang cân;

- Các đường thẳng chứa cạnh bên của hình chóp cụt đều cùng đi qua một điểm;

- Đường cao của hình chóp cụt đều thì vuông góc với hai đáy của hình chóp cụt đều đó.