Góc lượng giác và hệ thức Chasles - Toán 11

Góc (còn được gọi là góc hình học) là hình gồm hai tia chung gốc. Mỗi góc có một số đo, đơn vị đo góc (hình học) là độ.

Số đo của một góc (hình học) không vượt quá 180 độ.

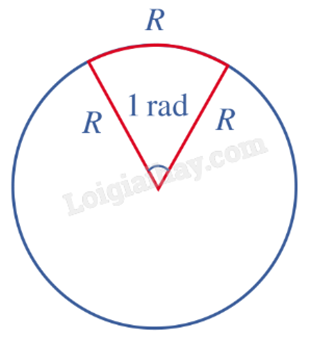
Một đơn vị khác được sử dụng nhiều khi đo góc là radian. Nếu trên đường tròn, ta lấy một cung tròn có độ dài bằng bán kính thì góc ở tâm chắn cung đó gọi là góc có số đo 1 radian.

Cho hai tia Oa và Ob.

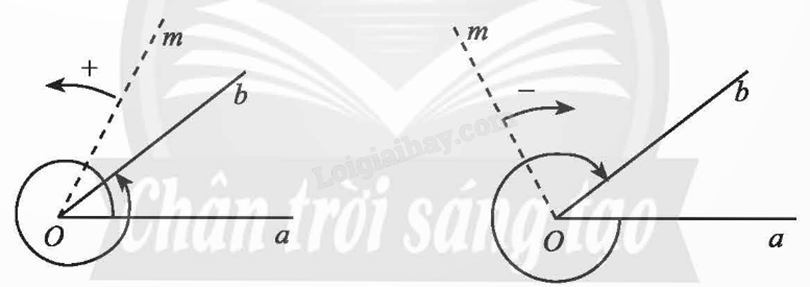
- Nếu một tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob, kí hiệu (Oa, Ob).

- Khi tia Om quay một góc \(\alpha \), ta nói số đo của góc lượng giác (Oa, Ob) bằng \(\alpha \), kí hiệu sđ(Oa, Ob) = \(\alpha \).

Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob sai khác nhau một bội nguyên của 360 độ nên ta có công thức tổng quát là:

\((Oa,Ob) = {\alpha ^o} + k{360^o}\)

với \({\alpha ^o}\) là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.

Với góc \(\alpha \) radian, ta có:

\((Oa,Ob) = \alpha  + k2\pi \).

Ví dụ minh hoạ:

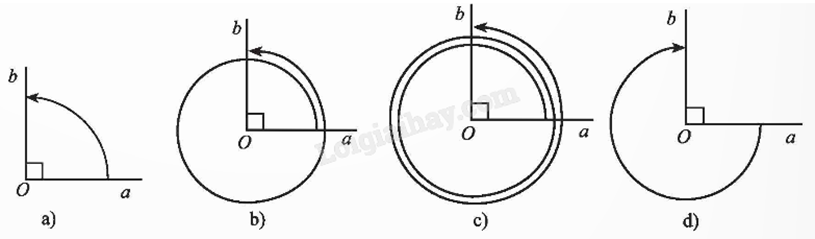
Xác định số đo của các góc lượng giác (Oa, Ob) trong hình.

Giải:

Số đo của góc lượng giác (Oa, Ob) hình a) là \({90^o}\).

Số đo của góc lượng giác (Oa, Ob) hình b) là \({90^o} + {360^o} = {450^o}\).

Số đo của góc lượng giác (Oa, Ob) hình c) là \({90^o} + {2.360^o} = {810^o}\).

Số đo của góc lượng giác (Oa, Ob) hình d) là \(\frac{3}{4}.( - {360^o}) =  - {270^o}\).

Với ba tia Oa, Ob, Oc bất kì, ta có:

\((Oa,Ob) + (Ob,Oc) = (Oa,Oc) + k{360^o}\) \((k \in \mathbb{Z})\);

hoặc \((Oa,Ob) + (Ob,Oc) = (Oa,Oc) + k2\pi \) \((k \in \mathbb{Z})\).

Ví dụ minh hoạ:

Cho góc lượng giác (Ou, Ov) có số đo là \(\frac{{3\pi }}{4}\), góc lượng giác (Ou, Ow) có số đo là \(\frac{{5\pi }}{4}\). Tìm số đo của góc lượng giác (Ov, Ow).

Giải:

Từ hệ thức Chasles, ta có:

\((Ov,Ow) = (Ou,Ow) - (Ou,Ov) + k2\pi \)

\( = \frac{{5\pi }}{4} - \frac{{3\pi }}{4} + k2\pi  = \frac{\pi }{2} + k2\pi \) \((k \in \mathbb{Z})\).