Đường tròn lượng giác và giá trị lượng giác - Toán 11

a) Khái niệm

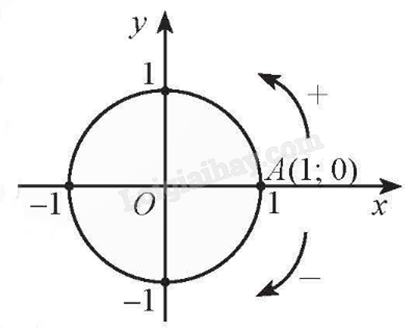
Trong mặt phẳng toạ độ Oxy, cho đường tròn tâm O bán kính bằng 1. Trên đường tròn này:

- Gốc: Điểm A(1;0).

- Chiều: (+) ngược chiều kim đồng hồ; (-) cùng chiều kim đồng hồ.

- Trục:

+ Trục cosin: Trục hoành Ox.

+ Trục sin: Trục tung Oy.

Đường tròn cùng với gốc và chiều như trên được gọi là đường tròn lượng giác.

b) Điểm biểu diễn

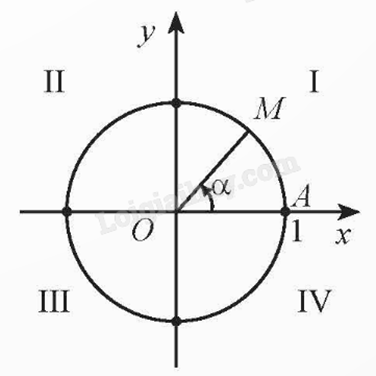
Cho số đo góc \(\alpha \) bất kì. Trên đường tròn lượng giác, ta xác định được duy nhất 1 điểm M sao cho \((OA,OM) = \alpha \).

M được gọi là điểm biểu diễn của góc có số đo \(\alpha \) trên đường tròn lượng giác.

c) Góc phần tư

Hệ trục toạ độ Oxy chia mặt phẳng toạ độ thành bốn “góc phần tư” kí hiệu lần lượt là I, II, III, IV.

Trên đường tròn lượng giác, gọi M là điểm biểu diễn góc lượng giác có số đo \(\alpha \). Khi đó:

- Tung độ \({y_M}\) của M gọi là sin của \(\alpha \), kí hiệu \(\sin \alpha \).

- Hoành độ \({x_M}\) của M gọi là cosin của \(\alpha \), kí hiệu \(\cos \alpha \).

- Nếu \({x_M} \ne 0\) thì tỉ số \(\frac{{{y_M}}}{{{x_M}}} = \frac{{\sin \alpha }}{{\cos \alpha }}\) gọi là tang của \(\alpha \), kí hiệu \(\tan \alpha \).

- Nếu \({y_M} \ne 0\) thì tỉ số \(\frac{{{x_M}}}{{{y_M}}} = \frac{{\cos \alpha }}{{\sin \alpha }}\) gọi là cotang của \(\alpha \), kí hiệu \(\cot \alpha \).

Các giá trị \(\sin \alpha \), \(\cos \alpha \), \(\tan \alpha \) và \(\cot \alpha \) được gọi là các giá trị lượng giác của góc lượng giác \(\alpha \).

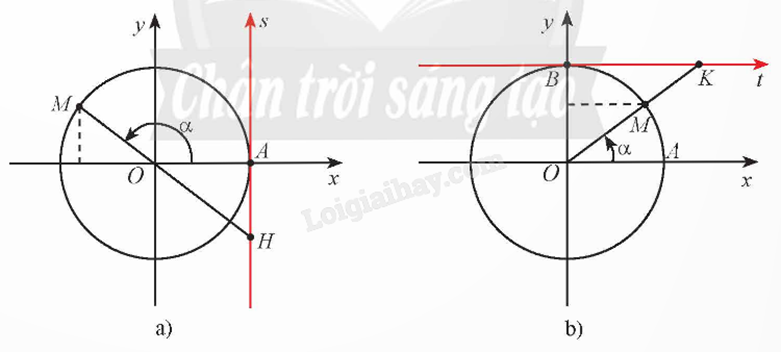
Chú ý:

+ Trục cosin: Trục hoành Ox.

+ Trục sin: Trục tung Oy.

+ Trục tang: Trục As có gốc ở điểm A(1;0) và song song với trục sin (trục Oy).

+ Trục cotang: Trục Bt có gốc ở điểm B(0;1) và song song với trục cos (trục Ox).

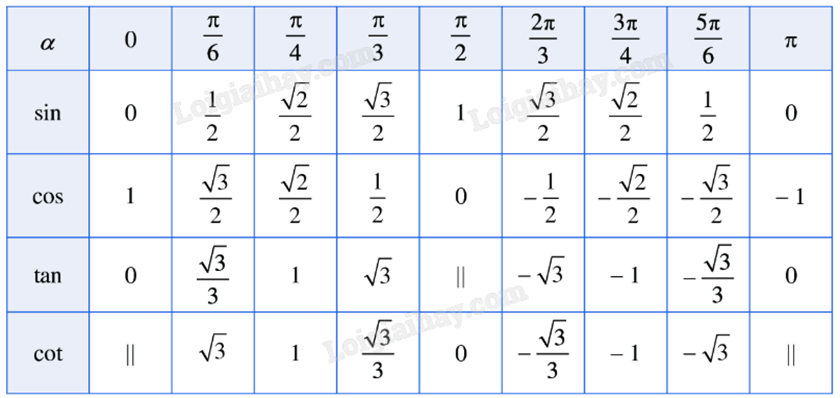
Bảng giá trị lượng giác của một số góc đặc biệt:

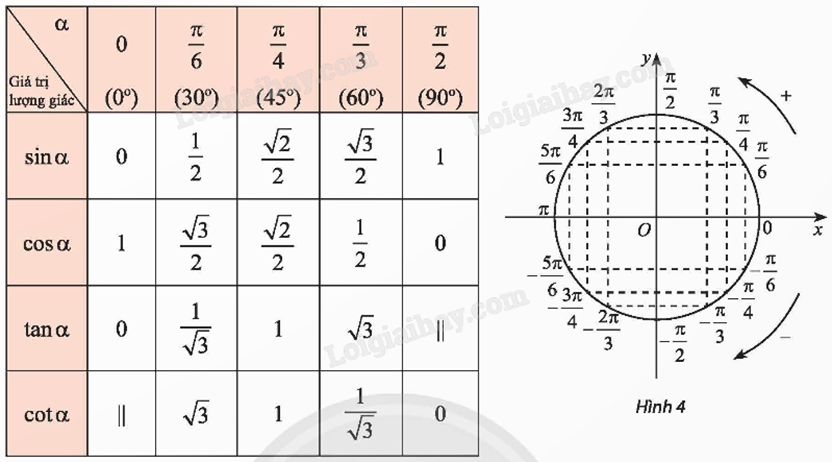
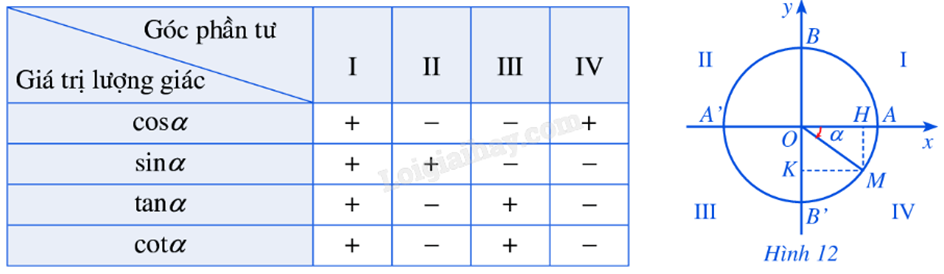
Dấu của các giá trị lượng giác của \(\alpha  = (OA,OM)\), phụ thuộc vào vị trí điểm M trên đường tròn lượng giác: