Giải mục 6 trang 46 Chuyên đề học tập Toán 10 - Cánh diều
Cho elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
HĐ 8
Cho elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
Xét đường tròn (C) tâm O bán kính a có phương trình \({x^2} + {y^2} = {a^2}\)
Cét điểm \(M\left( {x;y} \right) \in \left( E \right)\) và \({M_1}\left( {x;{y_1}} \right) \in \left( C \right)\) sao cho \(y\) và \({y_1}\) luôn cùng dấu (Khi M khác với hai đỉnh \({A_1},{A_2}\) của (E)) (Hình 10)
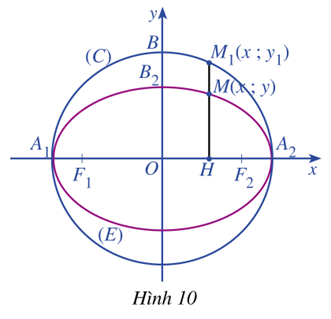
a) Từ phương trình chính tắc của elip (E), hãy tính \({y^2}\) theo \({x^2}\)
Từ phương trình của đường tròn (C), hãy tính \({y_1}^2\) theo \({x^2}\)
b) Tính tỉ số \(\frac{{HM}}{{H{M_1}}} = \frac{y}{{{y_1}}}\) theo \(a,b\)
Lời giải chi tiết:
a) Ta có \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow {y^2} = {b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right) = \frac{{\left( {{a^2} - {x^2}} \right){b^2}}}{{{a^2}}}\)
Tương tự, \({M_1}\left( {x;{y_1}} \right) \in \left( C \right)\) nên \({x^2} + {y_1}^2 = {a^2} \Rightarrow {y_1}^2 = {a^2} - {x^2}\)
b) Ta có: \(\frac{{{y^2}}}{{{y_1}^2}} = \frac{{\frac{{\left( {{a^2} - {x^2}} \right){b^2}}}{{{a^2}}}}}{{{a^2} - {x^2}}} = \frac{{{b^2}}}{{{a^2}}}\).
Vậy \(\frac{{HM}}{{H{M_1}}} = \frac{y}{{{y_1}}} = \frac{b}{a}\), tức là \({y_1} = \frac{a}{b}y\)
Bình luận
Chia sẻ
- Giải mục 7 trang 47 Chuyên đề học tập Toán 10 - Cánh diều
- Giải bài 1 trang 48 Chuyên đề học tập Toán 10 – Cánh diều
- Giải bài 2 trang 48 Chuyên đề học tập Toán 10 – Cánh diều
- Giải bài 3 trang 48 Chuyên đề học tập Toán 10 – Cánh diều
- Giải bài 4 trang 48 Chuyên đề học tập Toán 10 – Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
