 Giải chuyên đề học tập Toán lớp 11 Kết nối tri thức
Giải chuyên đề học tập Toán lớp 11 Kết nối tri thức
 Bài 2. Phép tịnh tiến Chuyên đề học tập Toán 11 kết nối..
Bài 2. Phép tịnh tiến Chuyên đề học tập Toán 11 kết nối..
Giải mục 2 trang 10, 11 Chuyên đề học tập Toán 11 - Kết nối tri thức
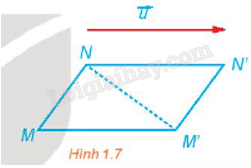
Phép tịnh tiến biến \({T_{\overrightarrow u }}\) iến M thành M', N thành N' (H.1.7).
Hoạt động 2
Phép tịnh tiến biến \({T_{\overrightarrow u }}\) iến M thành M', N thành N' (H.1.7).
a) Có nhận xét gì về \(\overrightarrow {MM'} + \overrightarrow {M'M} \) và \(\overrightarrow {M'N} + \overrightarrow {NN'} \)
b) Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {M'N'} \).
Phương pháp giải:
Quan sát hình vẽ, áp dụng quy tắc 3 điểm điểm làm.
Lời giải chi tiết:
a) Phép tịnh tiến \({T_{\overrightarrow u }}\) biến điểm M thành M' thì \(\overrightarrow {MM'} = \overrightarrow u \) và biến N thành N' thì \(\overrightarrow {NN'} = \vec u\).
Ta có: \(\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow u + \overrightarrow {M'N} \) và \(\overrightarrow {M'N} + \overrightarrow {NN'} = \overrightarrow {M'N} + \overrightarrow u \)
Do đó, \(\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {M'N} + \overrightarrow {NN'} \)
b) Theo quy tắc ba điểm ta có: \(\overrightarrow {MN} = \overrightarrow {MM'} + \overrightarrow {M'N} \) và \(\overrightarrow {M'N'} = \overrightarrow {M'N} + \overrightarrow {NN'} \)
Mà theo câu a) ta có: \(\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {M'N} + \overrightarrow {NN'} \)
Do đó, \(\overrightarrow {MN} = \overrightarrow {M'N'} \)
Luyện tập 2
Cho đường tròn (O; R) và điểm O' khác điểm O. Với mỗi điểm M thuộc (O; R) sao cho O, O', M không thẳng hàng, vẽ hình bình hành MOO'M'. Hỏi khi M thay đổi trên (O; R) thì M' thay đổi trên đường nào?
Phương pháp giải:
Vẽ hình và chứng minh M’ thay đổi trên trên đường tròn (O'; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Lời giải chi tiết:
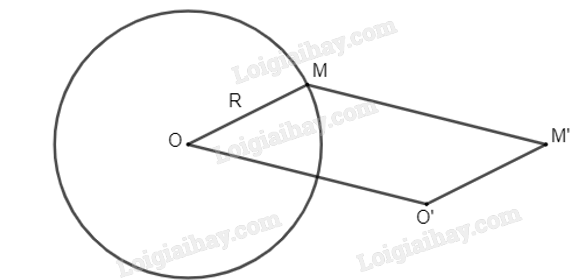
Ta có: MOO'M' là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {O'M'} \) và \(\overrightarrow {OO'} = \overrightarrow {MM'} \)
Vì OM = R nên \(O'M' = \left| {\overrightarrow {O'M'} } \right| = \left| {\overrightarrow {OM} } \right| = OM = R\) , R cố định nên O' luôn cách M' một khoảng không đổi bằng R.
Do O, O' cố định và \(\overrightarrow {OO'} = \overrightarrow {MM'} \) nên phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) biến điểm M thành điểm M'. Suy ra nếu M thay đổi trên (O; R) thì M' luôn là ảnh của điểm M qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Lại có phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) biến đường tròn (O; R) thành đường tròn có bán kính là R và có tâm là ảnh của tâm O qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) hay chính là điểm O'. Điều này có nghĩa là đường tròn (O'; R) là ảnh của đường tròn (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Mà O'M' = R không đổi nên M' luôn thuộc đường tròn (O'; R).
Vậy khi M thay đổi trên (O; R) thì M' thay đổi trên đường tròn (O'; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Vận dụng 2
Trong việc lát mặt phẳng bởi các tam giác đều bằng nhau như được thể hiện trong Hình 1.10, phép tịnh tiến theo vectơ \(\vec u\) có biến mỗi viên gạch màu xanh thành một viên gạch màu xanh, mỗi viên gạch màu đỏ thành một viên gạch màu đỏ hay không?

Phương pháp giải:
Quan sát hình vẽ, dựa vào định nghĩa: Cho vectơ \(\overrightarrow u \). Phép hiến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \) gọi là phép tịnh tiến theo \(\overrightarrow u \), kí hiệu \({T_{\overrightarrow u }}\). Vectơ \(\overrightarrow u \) được gọi là vectơ tịnh tiến.
Lời giải chi tiết:
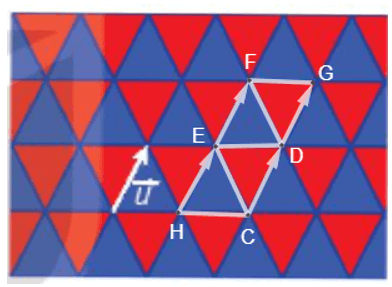
Đặt một số điểm như hình vẽ.
Ta thấy: \(\overrightarrow {HE} = \overrightarrow u ,\overrightarrow {CD} = \overrightarrow u ,\overrightarrow {EF} = \overrightarrow u \) nên phép tịnh tiến \({T_{\overrightarrow u }}\) biến các điểm H, C, E tương ứng thành E, D, F. Do đó, \({T_{\overrightarrow u }}\) biến tam giác HCE thành tam giác EDF hay phép tịnh tiến theo vectơ \(\overrightarrow u \) biến một viên gạch màu xanh thành một viên gạch màu xanh. Đối với các viên gạch màu xanh khác, thực hiện tương tự. Vậy phép tịnh tiến theo vectơ \(\overrightarrow u \) biến mỗi viên gạch màu xanh thành một viên gạch màu xanh.
Ta cũng có: \(\overrightarrow {CD} = \overrightarrow u ,\overrightarrow {DG} = \overrightarrow u ,\overrightarrow {EF} = \overrightarrow u \) nên phép tịnh tiến \({T_{\overrightarrow u }}\) biến các điểm C, D, E tương ứng thành D, G, F. Do đó, \({T_{\overrightarrow u }}\) biến tam giác CDE thành tam giác DGF hay phép tịnh tiến theo vectơ \(\overrightarrow u \) biến một viên gạch màu đỏ thành một viên gạch màu đỏ. Đối với các viên gạch màu đỏ khác, thực hiện tương tự. Vậy phép tịnh tiến theo vectơ \(\overrightarrow u \) biến mỗi viên gạch màu đỏ thành một viên gạch màu đỏ.
- Giải bài 1.3 trang 11 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 1.4 trang 11 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 1.5 trang 11 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải mục 1 trang 9, 10 Chuyên đề học tập Toán 11 - Kết nối tri thức
- Giải mở đầu trang 9 Chuyên đề học tập Toán 11 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 3.24 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 3.23 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 3.20 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 3.24 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 3.23 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 3.21 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức
- Giải bài 3.20 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức












Danh sách bình luận