Giải mục 1 trang 23, 24, 25 Chuyên đề học tập Toán 10 - Cánh diều

Câu hỏi khởi động

Chia hình vuông cạnh 1 thành 4 hình vuông nhỏ bằng nhau, lấy ra hình vuông nhỏ thứ nhất (ở góc dưới bên trái, màu đỏ), cạnh của hình vuông đó bằng $\frac{1}{2}.$

Chia hình vuông nhỏ ở góc trên bên phải thành bốn hình vuông bằng nhau, lấy ra hình vuông nhỏ thứ hai (màu đỏ), cạnh của hình vuông đó bằng $\frac{1}{4}.$

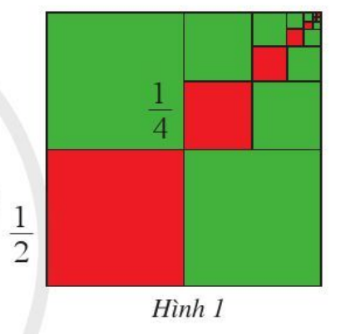
Tiếp tục quá trình trên ta được dãy các hình vuông nhỏ (màu đỏ) ở hình 1.

Cạnh của hình vuông nhỏ thứ n (màu đỏ) bằng bao nhiêu? Vì sao?

Lời giải chi tiết:

Nhận xét:

Chia hình vuông cạnh a thành 4 hình vuông, lấy ra hình vuông nhỏ thứ nhất (như cách lấy ở trên) thì cạnh của hình vuông đó bằng $\frac{a}{2}$.

=> Sau mỗi lần lấy, độ lớn của cạnh hình vuông giảm đi 2 lần

=> Sau n lần, cạnh hình vuông nhỏ thứ n giảm đi ${2^n}$ so với hình ban đầu.

=> Cạnh của hình vuông nhỏ thứ n là $\frac{1}{{{2^n}}}$

Hoạt động

Xét mệnh đề chứa biến P(n): “$1 + 3 + 5 + ... + (2n - 1) = {n^2}$” với n là số nguyên dương.

a) Chứng tỏ rằng P(1) là mệnh đề đúng.

b) Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, cho biết $1 + 3 + 5 + ... + (2k - 1)$ bằng bao nhiêu.

c) Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, chứng tỏ rằng P(k+1) cũng là mệnh đề đúng bằng cách chỉ ra ${k^2} + [2(k + 1) - 1] = {(k + 1)^2}$.

Lời giải chi tiết:

a) Mệnh đề P(1) là: “$1 = {1^2}$”, rõ ràng mệnh đề này đúng.

b) Mệnh đề P(k) là: “$1 + 3 + 5 + ... + (2k - 1) = {k^2}$”

Mệnh đề P(k) đúng thì $1 + 3 + 5 + ... + (2k - 1)$ bằng ${k^2}$

c) Mệnh đề P(k+1) là: “$1 + 3 + 5 + ... + [2(k + 1) - 1] = {(k + 1)^2}$”

Mệnh đề P(k) đúng nên ta có $1 + 3 + 5 + ... + (2k - 1) = {k^2}$

$\begin{array}{l} \Rightarrow 1 + 3 + 5 + ... + [2(k + 1) - 1] = 1 + 3 + 5 + ... + (2k - 1) + [2(k + 1) - 1]\\ = {k^2} + [2(k + 1) - 1] = {k^2} + 2k + 1 = {(k + 1)^2}\end{array}$

Vậy mệnh đề P(k+1) cũng đúng.

Luyện tập – vận dụng 1

Chứng minh:

a) $\frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + ... + \frac{1}{{\sqrt n  + \sqrt {n + 1} }} = \sqrt {n + 1}  - 1$ với mọi $n \in \mathbb{N}*$

b) $\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{n^3} - 1}}{{{n^3} + 1}} = \frac{{2({n^2} + n + 1)}}{{3n(n + 1)}}$ với mọi $n \in \mathbb{N}*,n \ge 2$

Phương pháp giải:

Chứng minh mệnh đề P(n) đúng với $n \ge p$ thì:

Bước 1: Chứng tỏ mệnh đề đúng với $n = p$

Bước 2: Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, ta chứng tỏ P(k+1) cũng là mệnh đề đúng.

Lời giải chi tiết:

a) Ta chứng minh bằng quy nạp theo n.

Bước 1: Khi $n = 1$ ta có $\frac{1}{{\sqrt 1  + \sqrt 2 }} = \sqrt 2  - 1$, đúng

vì $\left( {\sqrt 2  + \sqrt 1 } \right)\left( {\sqrt 2  - \sqrt 1 } \right) = 2 - 1 = 1 \Rightarrow \frac{1}{{\sqrt 2  + \sqrt 1 }} = \sqrt 2  - \sqrt 1  = \sqrt 2  - 1$

Như vậy đẳng thức đúng với $n = 1$

Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:

$\frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + ... + \frac{1}{{\sqrt {k + 1}  + \sqrt {k + 2} }} = \sqrt {k + 2}  - 1$

Thật vậy, theo giả thiết quy nạp ta có:

$\frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + ... + \frac{1}{{\sqrt k  + \sqrt {k + 1} }} = \sqrt {k + 1}  - 1$

Suy ra

$\begin{array}{l}\frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + ... + \frac{1}{{\sqrt {k + 1}  + \sqrt {k + 2} }}\\ = \sqrt {k + 1}  - 1 + \frac{1}{{\sqrt {k + 1}  + \sqrt {k + 2} }}\\ = \frac{{{{\left( {\sqrt {k + 1} } \right)}^2} + \sqrt {k + 1} .\sqrt {k + 2}  + 1}}{{\sqrt {k + 1}  + \sqrt {k + 2} }} - 1\\ = \frac{{k + 2 + \sqrt {k + 1} .\sqrt {k + 2} }}{{\sqrt {k + 1}  + \sqrt {k + 2} }} - 1\\ = \frac{{\sqrt {k + 2} \left( {\sqrt {k + 2}  + \sqrt {k + 1} } \right)}}{{\sqrt {k + 1}  + \sqrt {k + 2} }} - 1\\ = \sqrt {k + 2}  - 1\end{array}$

Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi $n \in \mathbb{N}*$. Tức là:

$\frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + ... + \frac{1}{{\sqrt n  + \sqrt {n + 1} }} = \sqrt {n + 1}  - 1$ với mọi $n \in \mathbb{N}*$

b) Ta chứng minh bằng quy nạp theo n.

Bước 1: Khi $n = 2$ ta có $\frac{{{2^3} - 1}}{{{2^3} + 1}} = \frac{{2({2^2} + 2 + 1)}}{{3.2(2 + 1)}}$, đúng

vì $\frac{{{2^3} - 1}}{{{2^3} + 1}} = \frac{7}{9};\frac{{2({2^2} + 2 + 1)}}{{3.2(2 + 1)}} = \frac{{2.7}}{{3.2.3}} = \frac{7}{9}$

Như vậy đẳng thức đúng với $n = 2$

Bước 2: Với k là một số nguyên dương lớn hơn 2 tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:

$\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}} = \frac{{2({{(k + 1)}^2} + (k + 1) + 1)}}{{3(k + 1)(k + 2)}}$

Thật vậy, theo giả thiết quy nạp ta có:

$\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}} = \frac{{2({{(k + 1)}^2} + (k + 1) + 1)}}{{3(k + 1)(k + 2)}}$

Suy ra

$\begin{array}{l}\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{[(k + 1) - 1][{{(k + 1)}^2} + (k + 1) + 1]}}{{[(k + 1) + 1][{{(k + 1)}^2} - (k + 1) + 1]}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{k[{{(k + 1)}^2} + (k + 1) + 1]}}{{(k + 2)({k^2} + 2k + 1 - k - 1 + 1)}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{k[{{(k + 1)}^2} + (k + 1) + 1]}}{{(k + 2)({k^2} + k + 1)}}\\ = \frac{{2[{{(k + 1)}^2} + (k + 1) + 1]}}{{3(k + 1)(k + 2)}}\end{array}$

Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi $n \in \mathbb{N}*,n \ge 2$. Tức là:

$\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{n^3} - 1}}{{{n^3} + 1}} = \frac{{2({n^2} + n + 1)}}{{3n(n + 1)}}$ với mọi $n \in \mathbb{N}*,n \ge 2$