Giải bài tập 3.15 trang 106 SGK Toán 12 tập 1 - Cùng khám phá

Hai bảng dưới đây biểu diễn kết quả đo đường kính (tính theo mm) của một số ổ bi được sản xuất bởi các máy X và Y:

Đề bài

Hai bảng dưới đây biểu diễn kết quả đo đường kính (tính theo mm) của một số ổ bi được sản xuất bởi các máy X và Y:

a) Ước tính giá trị trung bình và độ lệch chuẩn của đường kính các ổ bi được sản xuất bởi mỗi máy.

b) Biết rằng đường kính mong muốn cho các ổ bi là 30,4 mm. Hãy phân tích chất lượng sản phẩm do mỗi máy sản xuất.

Phương pháp giải - Xem chi tiết

a) Áp dụng các công thức sau:

- Công thức tính trung bình:

\(\bar x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)

- Công thức tính độ lệch chuẩn:

\(S = \sqrt {\overline {{x^2}} - {{\left( {\bar x} \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\bar x} \right)}^2}} \)

b) So sánh giá trị trung bình và độ lệch chuẩn với giá trị mong muốn (30,4 mm) để đánh giá sự chính xác và độ phân tán của sản phẩm.

Lời giải chi tiết

Bảng phân phối tần số cho máy X và Y:

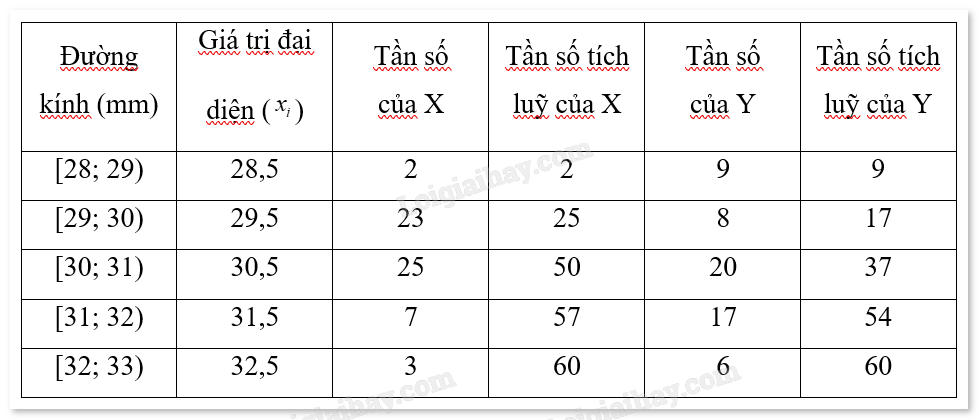
Dựa vào bảng phân phối ta thấy N = 60.

Giá trị trung bình của máy X:

\({\bar x_X} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{2 \times 28,5 + 23 \times 29,5 + 25 \times 30,5 + 7 \times 31,5 + 3 \times 32,5}}{{60}} = \frac{{1816}}{{60}} \approx 30,27\)

Độ lệch chuẩn của máy X:

\({S_X} = \sqrt {\overline {x_X^2} - {{\left( {{{\bar x}_X}} \right)}^2}} \)

\(\overline {x_X^2} = \frac{{\sum {{f_i}x_i^2} }}{N} = \frac{{2 \times 28,{5^2} + 23 \times 29,{5^2} + 25 \times 30,{5^2} + 7 \times 31,{5^2} + 3 \times 32,{5^2}}}{{60}} = \frac{{55011}}{{60}} = 916,85\)

\({S_X} = \sqrt {916,85 - 30,{{27}^2}} = \sqrt {0,78} \approx 0,88\)

Giá trị trung bình của máy Y:

\({\bar x_Y} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{9 \times 28,5 + 8 \times 29,5 + 20 \times 30,5 + 17 \times 31,5 + 6 \times 32,5}}{{60}} = \frac{{1833}}{{60}} = 30,55\)

Độ lệch chuẩn của phương pháp B:

\({S_Y} = \sqrt {\overline {x_Y^2} - {{\left( {{{\bar x}_Y}} \right)}^2}} \)

\(\overline {x_Y^2} = \frac{{\sum {{f_i}x_i^2} }}{N} = \frac{{9 \times 28,{5^2} + 8 \times 29,{5^2} + 20 \times 30,{5^2} + 17 \times 31,{5^2} + 6 \times 32,{5^2}}}{{60}} = \frac{{56083}}{{60}} \approx 934,72\)

\({S_Y} = \sqrt {934,72 - 30,{{55}^2}} = \sqrt {1,4175} \approx 1,19\)

Phân tích chất lượng sản phẩm:

- Máy X: Như đã tính trước đó, giá trị trung bình là 30.27 mm và độ lệch chuẩn là 0.88 mm.

- Máy Y: Với giá trị trung bình mới là 30.55 mm và độ lệch chuẩn là 1.19 mm.

Kết luận:

- Máy X sản xuất sản phẩm có đường kính trung bình gần với giá trị mong muốn hơn (30,27 mm so với 30,4 mm), với độ lệch chuẩn nhỏ hơn, cho thấy sản phẩm đều hơn.

- Máy Y có giá trị trung bình lớn hơn 30,4 mm (30,55 mm), và độ lệch chuẩn cũng lớn hơn, cho thấy sản phẩm có sự biến thiên lớn hơn về kích thước, chất lượng không đồng đều bằng sản phẩm của máy X.

Do đó, sản phẩm của máy X vẫn được đánh giá là có chất lượng tốt hơn so với máy Y.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 3.16 trang 106 SGK Toán 12 tập 1 - Cùng khám phá
Khoảng biến thiên của mẫu số liệu cho bởi Bảng 3.30 là: A. 2 B. 3 C. 4 D. 5
Giải bài tập 3.17 trang 106 SGK Toán 12 tập 1 - Cùng khám phá
Gọi \({\Delta _Q}\) là khoảng tứ phân vị của mẫu số liệu cho bởi Bảng 3.30. Khi đó A. \({\Delta _Q} \in [1;2)\). B. \({\Delta _Q} \in [2;3)\). C. \({\Delta _Q} \in [3;4)\). D. \({\Delta _Q} \in [4;5)\).
Giải bài tập 3.18 trang 106 SGK Toán 12 tập 1 - Cùng khám phá
Phương sai của mẫu số liệu cho bởi bảng 3.30 là A. \({s^2} = \frac{8}{{15}} - {\left( {\frac{7}{{15}}} \right)^2}\). B. \({s^2} = \frac{{233}}{{15}} - {\left( {\frac{{50}}{{15}}} \right)^2}\). C. \({s^2} = \frac{8}{{15}} - {\left( {\frac{{57}}{{15}}} \right)^2}\). D. \({s^2} = \frac{{233}}{{15}} - {\left( {\frac{{57}}{{15}}} \right)^2}\).
Giải bài tập 3.19 trang 106 SGK Toán 12 tập 1 - Cùng khám phá
Trong các khẳng định sau, khẳng định nào sai? A. Phương sai luôn luôn là số không âm. B. Phương sai là bình phương của độ lệch chuẩn. C. Phương sai càng lớn thì độ phân tán của các giá trị quanh số trung bình càng lớn. D. Phương sai luôn luôn lớn hơn độ lệch chuẩn.
Giải bài tập 3.13 trang 104 SGK Toán 12 tập 1 - Cùng khám phá
Một công ty giống cây trồng đã thử nghiệm hai phương pháp chăm sóc khác nhau cho cây hướng dương. Sau hai tuần, người ta thấy cây được chăm sóc theo cả hai phương pháp đều thấp hơn 50 cm. Hình 3.5a và 3.5b biểu diễn chiều cao của một số cây.
Giải bài tập 3.12 trang 104 SGK Toán 12 tập 1 - Cùng khám phá
Hàm lượng protein (trong 100g) của một số loại thực phẩm được cho trong bảng sau:
Giải bài tập 3.11 trang 104 SGK Toán 12 tập 1 - Cùng khám phá
Một trang trại phân 1000 quả trứng thành 5 loại, tuỳ theo khối lượng (đã được làm tròn) của chúng (Bảng 3.26).
Giải bài tập 3.10 trang 104 SGK Toán 12 tập 1 - Cùng khám phá
Chiều cao của 500 học sinh một trường trung học cơ sở được thống kê trong Bảng 3.25.