-
Giải Toán 12 tập 1 - Cùng khám phá
-
Giải Toán 12 tập 2 - Cùng khám phá
-
Nội dung đang cập nhật
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Bài tập cuối chương 1 - Toán 12 Cùng khám phá
Giải bài tập 1.39 trang 47 SGK Toán 12 tập 1 - Cùng khám phá
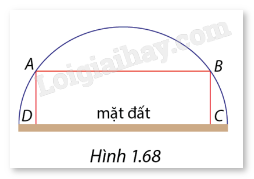
Một cổng vòm có dạng nửa hình tròn trên mặt đất với bán kính R=5 m. Người ta muốn đặt một khung hình chữ nhật ABCD để thiết kế trang trí, với hai điểm A,B đính trên vòm và CD đặt trên mặt đất (Hình 1.68). Tìm khoảng cách A,B so với mặt đất để diện tích hình chữ nhật ABCD là lớn nhất.
Đề bài
Một cổng vòm có dạng nửa hình tròn trên mặt đất với bán kính R=5 m. Người ta muốn đặt một khung hình chữ nhật ABCD để thiết kế trang trí, với hai điểm A,B đính trên vòm và CD đặt trên mặt đất (Hình 1.68). Tìm khoảng cách A,B so với mặt đất để diện tích hình chữ nhật ABCD là lớn nhất.
Phương pháp giải - Xem chi tiết
- Đặt y (m) là khoảng cách từ AB đến mặt đất. Vì A và B nằm trên vòm nửa hình tròn có bán kính R=5 m, nên tọa độ của A và B có thể biểu diễn dưới dạng (x,y).
- Tìm phương trình đường tròn và tính diện tích S của hình chữ nhật ABCD.
- Biểu diễn S dưới dạng một hàm của y và cực đại hóa S bằng cách tìm đạo hàm.
Lời giải chi tiết
Gọi y (m) là khoảng cách từ A và B đến mặt đất (y>0).
Vì A và B nằm trên nửa hình tròn có tâm tại gốc tọa độ (0,0) và bán kính R=5 m, tọa độ của chúng thỏa mãn phương trình đường tròn:
\({x^2} + {y^2} = 25\)
Giả sử A có toạ độ \(( - x,y)\) và B có toạ độ \((x,y)\).
Chiều dài AB là: \(\sqrt {{{( - x - x)}^2} + {{(y - y)}^2}} = 2x\)
Diện tích hình chữ nhật ABCD là: \(S = AB.AD = 2xy\)
Thay \(x = \sqrt {25 - {y^2}} \) vào biểu thức diện tích ta được: \(S = 2\sqrt {25 - {y^2}} .y\)
Đạo hàm của S theo y: \(\)\(S' = 2\left( {\sqrt {25 - {y^2}} + y.\frac{{ - y}}{{\sqrt {25 - {y^2}} }}} \right) = 2\left( {\frac{{25 - {y^2} - {y^2}}}{{\sqrt {25 - {y^2}} }}} \right) = 2\left( {\frac{{25 - 2{y^2}}}{{\sqrt {25 - {y^2}} }}} \right)\)
Đặt đạo hàm bằng 0, ta có: \(S' = 0 \Leftrightarrow 25 - 2{y^2} = 0 \Leftrightarrow 2{y^2} = 25 \Rightarrow y = \frac{{5\sqrt 2 }}{2}\)
Đạo hàm cấp 2 của S:
\(\begin{array}{l}S'' = 2.\frac{{ - 4y.\sqrt {25 - {y^2}} + (25 - 2{y^2})\frac{y}{{\sqrt {25 - {y^2}} }}}}{{25 - {y^2}}}\\ = 2.\frac{{ - 4y\sqrt {25 - {y^2}} + \frac{{y\left( {25 - 2{y^2}} \right)}}{{\sqrt {25 - {y^2}} }}}}{{25 - {y^2}}}\\ = 2.\frac{{ - 4y\left( {25 - {y^2}} \right) + y\left( {25 - 2{y^2}} \right)}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\\ = 2.\frac{{ - 4y\left( {25 - {y^2}} \right) + y\left( {25 - 2{y^2}} \right)}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\\ = 2.\frac{{ - 100y + 4{y^3} + 25y - 2{y^3}}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\\ = 2.\frac{{ - 75y + 2{y^3}}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\end{array}\)
Thay \(y = \frac{{5\sqrt 2 }}{2}\) vào đạo hàm cấp 2 ta được:
\(S''\left( {\frac{{5\sqrt 2 }}{2}} \right) = 2.\frac{{ - 75.\left( {\frac{{5\sqrt 2 }}{2}} \right) + 2{{\left( {\frac{{5\sqrt 2 }}{2}} \right)}^3}}}{{\left( {25 - {{\left( {\frac{{5\sqrt 2 }}{2}} \right)}^2}} \right)\sqrt {25 - {{\left( {\frac{{5\sqrt 2 }}{2}} \right)}^2}} }} = - 8 < 0\)
Vì giá trị âm nên \(y = \frac{{5\sqrt 2 }}{2}\)là cực đại của hàm S.
Vậy A, B cách mặt đất một khoảng \(y = \frac{{5\sqrt 2 }}{2}\) thì diện tích hình chữ nhật ABCD là lớn nhất.
Bình luận
Chia sẻ
- Giải bài tập 1.40 trang 47 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.41 trang 47 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.42 trang 48 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.43 trang 48 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.44 trang 48 SGK Toán 12 tập 1 - Cùng khám phá
>> Xem thêm
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
Các bài khác cùng chuyên mục
