Giải bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2

Cho tam giác nhọn ABC ((widehat B > widehat C)), phân giác AM. Gọi O, O1, O2 lần lượt là tâm đường tròn ngoại tiếp các tam giác ABC, AMB, AMC. Chứng minh rằng: a) OO1, OO2, O1O2 lần lượt là các đường trung trực của AB, AC, AM; b) Tam giác OO1O2 cân.

Đề bài

Cho tam giác nhọn ABC (\(\widehat B > \widehat C\)), phân giác AM. Gọi O, O₁, O₂ lần lượt là tâm đường tròn ngoại tiếp các tam giác ABC, AMB, AMC. Chứng minh rằng:

a) OO₁, OO₂, O₁O₂ lần lượt là các đường trung trực của AB, AC, AM;

b) Tam giác OO₁O₂ cân.

Phương pháp giải - Xem chi tiết

Dựa vào khoảng cách từ tâm đến các điểm đường tròn bằng nhau.

Chứng minh \(\widehat {{\rm{O}}{{\rm{O}}_1}{O_2}} = \widehat {{\rm{O}}{{\rm{O}}_2}{O_1}}\) để suy ra tam giác OO₁O₂ cân.

Lời giải chi tiết

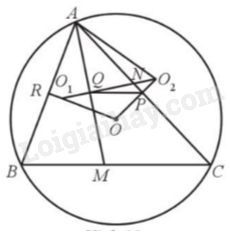
a) Do OA = OB và O₁A = O₁B nên OO₁ là đường trung trực của AB.

Tương tự OO₂, O₁O₂ lần lượt là các đường trung trực của AC, AM.

b) Gọi P, Q, R lần lượt là trung điểm của AC, AM, AB; N là giao điểm của QO₂ và AC. Ta có \(\widehat {{\rm{O}}{{\rm{O}}_1}Q} = \widehat {RAQ} = \frac{{\widehat {BAC}}}{2}( = {180^o} - \widehat {R{O_1}Q})\) (1).

Mặt khác \(\widehat {{{\rm{O}}_2}NP} = \widehat {ANQ}\) nên \({90^o} - \widehat {{{\rm{O}}_2}NP} = {90^o} - \widehat {ANQ}\).

Suy ra: \(\widehat {N{O_2}P} = \widehat {QAN} = \frac{{\widehat {BAC}}}{2}\) (2).

Từ (1) và (2) suy ra \(\widehat {{\rm{O}}{{\rm{O}}_1}{O_2}} = \widehat {{\rm{O}}{{\rm{O}}_2}{O_1}}\). Do đó, tam giác OO₁O₂ cân tại O.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 7 trang 85 sách bài tập toán 9 - Cánh diều tập 2
Trên đường tròn (O) bán kính R, lấy các điểm A, B, C, D sao cho (sđoversetfrown{AB}={{60}^{o}}); (sđoversetfrown{BC}={{90}^{o}}); (sđoversetfrown{CD}={{120}^{o}}) (Hình 7). a) Xác định tâm và tính theo R bán kính đường tròn ngoại tiếp của các tam giác OAB, OBC, OAD, OCD. b) Gọi I là giao điểm của AC và BD. Tính bán kính đường tròn ngoại tiếp của các tam giác IAB, IBC, IAD, IDC.
Giải bài 8 trang 86 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC vuông tại A có AB = 6, AC = 8, bán kính đường tròn nội tiếp là r, bán kính đường tròn ngoại tiếp là R. Tính (frac{r}{R}).
Giải bài 9 trang 86 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính R. a) Chứng minh rằng O cũng là tâm đường tròn nội tiếp tam giác ABC. b) Vẽ tam giác IJK ngoại tiếp đường tròn (O; R) với JK // BC, IJ // AC, IK // AB. Chứng minh tam giác IJK đều. c) Gọi R’ là bán kính của đường tròn ngoại tiếp tam giác IJK và r là bán kính của đường tròn nội tiếp tam giác ABC. Tính (frac{r}{{R'}}).
Giải bài 10 trang 86 sách bài tập toán 9 - Cánh diều tập 2
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm phân biệt A, B. Đường thẳng AO cắt (O) và (O’) lần lượt tại hai điểm C, E (khác điểm A). Đường thẳng AO’ cắt (O) và (O’) lần lượt tại hai điểm D, F (khác điểm A). Chứng minh: a) C, B, F thẳng hàng; b) Bốn điểm C, D, E, F cùng nằm trên một đường tròn; c) A là tâm đường tròn nội tiếp tam giác BDE.
Giải bài 11 trang 86 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O; R). E là điểm tuỳ ý trên cung nhỏ AC của đường tròn đó. Gọi F là giao điểm của EB và CO, I là tâm đường tròn ngoại tiếp tam giác ECF. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì I luôn di chuyển trên một đoạn thẳng cố định.
Giải bài 5 trang 85 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau tại K. Tìm tâm đường tròn ngoại tiếp mỗi tam giác sau: a) Tam giác BDE; b) Tam giác DEC c) Tam giác ADE.
Giải bài 4 trang 85 sách bài tập toán 9 - Cánh diều tập 2
Vẽ đường tròn (O) ngoại tiếp tam giác MNP trong các trường hợp sau: a) (widehat M,widehat N,widehat P) đều nhọn; b) (widehat M = {90^o}) c) (widehat M > {90^o})
Giải bài 3 trang 85 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC cân tại A có O, I lần lượt là tâm các đường tròn ngoại tiếp và đường tròn nội tiếp tam giác ABC. a) Chứng minh rằng: - Ba điểm A, O, I cùng thuộc một đường thẳng; - Đường thẳng OA vuông góc với BC và đi qua điểm chính giữa D (khác điểm A) của cung BC. b) Cho BC = 24 cm, AC = 20 cm. Tính độ dài bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.
Giải bài 2 trang 84 sách bài tập toán 9 - Cánh diều tập 2
Tìm phát biểu sai trong các phát biểu sau: a) Trong một tam giác đều, trọng tâm của tam giác đồng thời là tâm của đường tròn nội tiếp tam giác. b) Trong một tam giác đều, trọng tâm của tam giác đồng thời là tâm của đường tròn ngoại tiếp tam giác. c) Tam giác đều cạnh a có bán kính đường tròn ngoại tiếp là (R = frac{{asqrt 3 }}{6}). d) Tam giác đều cạnh a có bán kính đường tròn nội tiếp là (r = frac{{asqrt 3 }}{3}).
Giải bài 1 trang 84 sách bài tập toán 9 - Cánh diều tập 2
Tìm phát biểu đúng trong các phát biểu sau: a) Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường phân giác của tam giác đó. b) Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó. c) Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền.