Giải bài 4 trang 85 sách bài tập toán 9 - Cánh diều tập 2
Vẽ đường tròn (O) ngoại tiếp tam giác MNP trong các trường hợp sau: a) (widehat M,widehat N,widehat P) đều nhọn; b) (widehat M = {90^o}) c) (widehat M > {90^o})
Đề bài
Vẽ đường tròn (O) ngoại tiếp tam giác MNP trong các trường hợp sau:
a) \(\widehat M,\widehat N,\widehat P\) đều nhọn;
b) \(\widehat M = {90^o}\)
c) \(\widehat M > {90^o}\)
Phương pháp giải - Xem chi tiết
Dựa vào đường tròn đi qua 3 đỉnh của tam giác được gọi là đường tròn ngoại tiếp tam giác đó.
Lời giải chi tiết
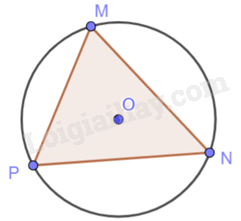
a) \(\widehat M,\widehat N,\widehat P\) đều nhọn
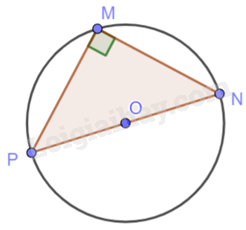
b) \(\widehat M = {90^o}\)
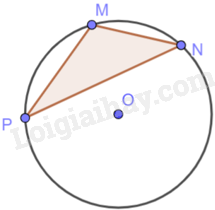
c) \(\widehat M > {90^o}\)
- Giải bài 5 trang 85 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 7 trang 85 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 8 trang 86 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 9 trang 86 sách bài tập toán 9 - Cánh diều tập 2
>> Xem thêm
Các bài khác cùng chuyên mục













Danh sách bình luận