Giải bài 5 trang 89 sách bài tập toán 11 - Cánh diều

*: Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tính góc giữa hai đường thẳng AD và BC

Đề bài

Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tính góc giữa hai đường thẳng AD và BC, biết \(MN = a\sqrt 3 \) và \(AD{\rm{ }} = {\rm{ }}BC = 2a.\)

Phương pháp giải - Xem chi tiết

Dựa vào các cách xác định góc giữa hai đường thẳng đã học để làm.

Lời giải chi tiết

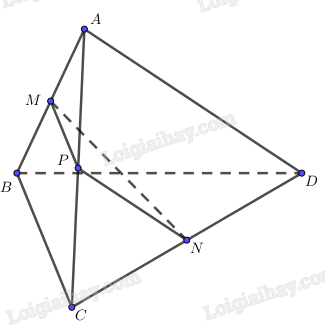
Gọi P là trung điểm của AC.

Ta có: MP, PN lần lượt là đường trung bình của \(\Delta ABC,\Delta ACD.\)

\( \Rightarrow MP//BC,{\rm{ }}PN//AD\) và \(MP = \frac{1}{2}BC = a,{\rm{ }}PN = \frac{1}{2}AD = a.\)

Do đó \(\left( {AD,BC} \right) = \left( {PN,MP} \right).\)

Xét \(\Delta MNP:\)

\(cos\widehat {MPN} = \frac{{M{P^2} + P{N^2} - M{N^2}}}{{2MP.PN}} = \frac{{{a^2} + {a^2} - {{\left( {a\sqrt 3 } \right)}^2}}}{{2a.a}} = - \frac{1}{2} \Rightarrow \widehat {MPN} = {120^0}.\)

Suy ra \(\left( {AD,BC} \right) = \left( {PN,MP} \right) = {180^0} - \widehat {MPN} = {180^0} - {120^0} = {60^0}.\)

Vậy góc giữa hai đường thẳng AD và BC là 60⁰.