Giải bài 5 trang 102 sách bài tập toán 9 - Cánh diều tập 1

Cho hai đường tròn (O) và (O') có bán kính bằng nhau, cắt nhau tại A và B. Chứng minh tứ giác OAO'B là hình thoi; từ đó, suy ra AB cắt OO' tại trung điểm của mỗi đường.

Đề bài

Cho hai đường tròn (O) và (O') có bán kính bằng nhau, cắt nhau tại A và B. Chứng minh tứ giác OAO'B là hình thoi; từ đó, suy ra AB cắt OO' tại trung điểm của mỗi đường.

Phương pháp giải - Xem chi tiết

Dựa vào dấu hiệu nhận biết: Tứ giác có 4 cạnh bằng nhau là hình thoi.

Lời giải chi tiết

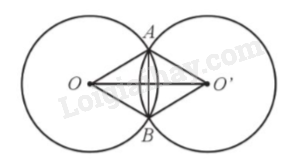
Vì hai đường tròn (O) và (O') có bán kính bằng nhau, suy ra \(OA = OB = O'A = O'B\).

Xét tứ giác OAO’B có: \(OA = OB = O'A = O'B\) nên OAO’B là hình thoi, do đó 2 đường chéo AB và OO’ cắt nhau tại trung điểm mỗi đường.

Bình luận

Chia sẻ

Bình chọn:

4 trên 5 phiếu

Bài tiếp theo

Giải bài 6 trang 103 sách bài tập toán 9 - Cánh diều tập 1
Hình 7 mô tả công trình xây dựng cây cầu bắc qua một hồ nước với mặt hồ có dạng hình tròn tâm O bán kính 2 km. Cây cầu có hai đầu cầu là hai điểm A, B nằm trên đường tròn tâm O. Tính chiều dài của cây cầu để khoảng cách từ tâm O của hồ nước đến cây cầu là OH = 1732 m (làm tròn kết quả đến hàng đơn vị của mét).
Giải bài 7 trang 103 sách bài tập toán 9 - Cánh diều tập 1
Hai hòn đảo được xem như hai hình tròn có khoảng cách từ tâm hòn đảo này đến tâm hòn đảo kia là khoảng 950 m. Biết rằng hòn đảo lớn có bán kính khoảng 500 m, còn đảo nhỏ có bán kính khoảng 300 m. Người ta cần xây dựng một cây cầu bắc từ đảo này sang đảo kia. Hãy chọn vị trí để xây cầu sao cho chiều dài cây cầu là ngắn nhất, khi đó tính chiều dài cây cầu.
Giải bài 8 trang 103 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn tâm O bán kính OA và đường tròn tâm O' đường kính OA. a) Xét vị trí tương đối của hai đường tròn (O) và (O'). b) Dây AD của đường tròn (O) cắt đường tròn (O’) tại C. Chứng minh AC = CD.
Giải bài 9 trang 103 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn (O; 3 cm) và (O'; 2 cm) tiếp xúc ngoài với nhau tại A. Một đường thẳng đi qua A cắt (O) và (O') lần lượt tại B và C (B và C khác A).
Giải bài 10 trang 103 sách bài tập toán 9 - Cánh diều tập 1
Trong mỗi hình 8a, 8h, 8c, các bánh xe tròn có răng cưa được khớp với nhau. Hình nào có hệ thống bánh răng chuyển động được? Hình nào có hệ thống bánh răng không chuyển động được?
Giải bài 4 trang 102 sách bài tập toán 9 - Cánh diều tập 1
Cho hai đường tròn (O; 17cm) và (O'; 10cm) cắt nhau tại A và B. Biết OO' = 21cm. Tính độ dài đoạn thẳng AB.
Giải bài 3 trang 102 sách bài tập toán 9 - Cánh diều tập 1
Cho hai đường tròn (O; 3,5 cm) và (O'; 4,5 cm). Tìm độ dài OO’ sao cho hai đường tròn đó tiếp xúc ngoài.
Giải bài 2 trang 102 sách bài tập toán 9 - Cánh diều tập 1
Cho hai đường tròn (O; 4 cm), (O'; 1 cm). Xét vị trí tương đối của hai đường tròn trong mỗi trường hợp sau: a) OO’ = 4,5cm b) OO’ = 6cm c) OO’ = 2cm
Giải bài 1 trang 102 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn (O; 25cm). Tính độ dài dây lớn nhất của đường tròn đó.