Giải bài 31 trang 108 sách bài tập toán 11 - Cánh diều

Cho hai hình bình hành \(ABCD\) và \(ABEF\) nằm trong hai mặt phẳng phân biệt.

Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Cánh diều

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Cho hai hình bình hành \(ABCD\) và \(ABEF\) nằm trong hai mặt phẳng phân biệt. Khẳng định nào sau đây là đúng?

A. \(\left( {ADF} \right)\parallel \left( {BCE} \right)\)

B. \(AD\parallel \left( {BEF} \right)\)

C. \(\left( {ABC} \right)\parallel \left( {DEF} \right)\)

D. \(EC\parallel \left( {ABD} \right)\)

Phương pháp giải - Xem chi tiết

Sử dụng các tính chất về đường thẳng song song với mặt phẳng, hai mặt phẳng song song.

Lời giải chi tiết

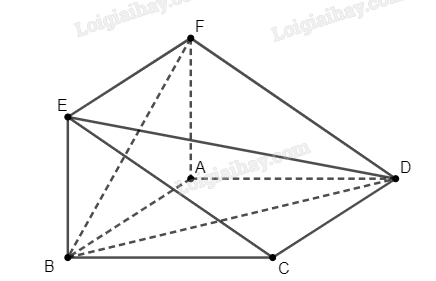
Do \(ABCD\) là hình bình hành nên \(AD\parallel BC\). Mà \(BC \subset \left( {BCE} \right)\), ta suy ra \(AD\parallel \left( {BCE} \right)\). Chứng minh tương tự ta có \(AF\parallel \left( {BCE} \right)\). Như vậy \(\left( {ADF} \right)\parallel \left( {BCE} \right)\).

Ta có \(A \in AD\), \(A \in \left( {BEF} \right)\) nên suy ra \(AD\) và \(\left( {BEF} \right)\) có điểm chung, tức là chúng không song song với nhau.

Tương tự, ta cũng chứng minh được \(EC\) và \(\left( {ABD} \right)\) không song song với nhau.

Do \(AB\parallel CD\), \(AB\parallel EF\) nên \(CD\parallel EF\), tức là tứ giác \(CDFE\) là hình bình hành.

Vì \(C \in \left( {ABC} \right)\), \(C \in \left( {DEF} \right)\), nên hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {DEF} \right)\) có điểm chung, tức là chúng không song song với nhau.

Đáp án đúng là A.