-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
Giải bài 30 trang 56 SBT toán 10 - Cánh diều
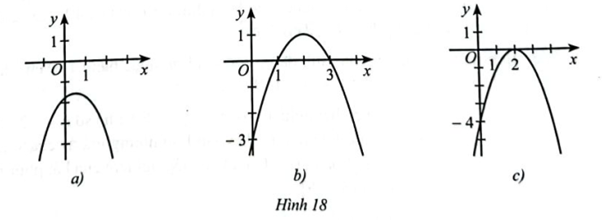
Dựa vào đồ thị hàm số bậc hai \(y = f\left( x \right)\) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: \(f\left( x \right) > 0;f\left( x \right) < 0;f\left( x \right) \ge 0;f\left( x \right) \le 0\)
Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Dựa vào đồ thị hàm số bậc hai \(y = f\left( x \right)\) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: \(f\left( x \right) > 0;f\left( x \right) < 0;f\left( x \right) \ge 0;f\left( x \right) \le 0\)
Phương pháp giải - Xem chi tiết
Phần đồ thị nằm dưới trục hoành tương ứng với \(f(x) < 0\)
Phần đồ thị nằm trên trục hoành tương ứng với \(f(x) > 0\)
Dựa vào parabol \(y = a{x^2} + bx + c\), ta tìm tập hợp những giá trị của \(x\) ứng với phần trên hoặc dưới trục hoành tùy dấu của tam thức bậc hai
Lời giải chi tiết
a) Quan sát đồ thị ở Hình 18a, ta có đồ thị hàm số \(y = f(x)\) nằm phía dưới trục hoành và không cắt trục hoành nên \(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\). Do đó:
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \mathbb{R}\)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \mathbb{R}\)
b) Quan sát đồ thị ở Hình 18b, ta có:
Phần đồ thị nằm trên trục hoành ứng với \(1 < x < 3\)
Phần đồ thị nằm dưới trục hoành ứng với \(x < 1\) và \(x > 3\)
Đồ thị cắt trục hoành tại điểm có hoành độ \(x = 1\) và \(x = 3\)
Kết luận
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \left( {1;3} \right)\)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = \left[ {1;3} \right]\)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
c) Quan sát đồ thị ở Hình 18c, ta có đồ thị hàm số \(y = f(x)\) nằm phía dưới trục hoành và cắt trục hoành tại A(2;0) nên \(f\left( x \right) \le 0\) với mọi \(x \in \mathbb{R}\).
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \mathbb{R}{\rm{\backslash }}\{ 2\} \)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = 2\)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \mathbb{R}\)
Bình luận
Chia sẻ
- Giải bài 31 trang 56 SBT toán 10 - Cánh diều
- Giải bài 32 trang 57 SBT toán 10 - Cánh diều
- Giải bài 33 trang 57 SBT toán 10 - Cánh diều
- Giải bài 34 trang 57 SBT toán 10 - Cánh diều
- Giải bài 35 trang 57 SBT toán 10 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
