 Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức
Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức
 Khảo sát và vẽ đồ thị hàm số với phần mềm GeoGebra - To..
Khảo sát và vẽ đồ thị hàm số với phần mềm GeoGebra - To..
Giải bài 3 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: a) (y = {x^3} - 3{x^2} - 9x + 35) trên đoạn (left[ { - 4;4} right]). b) (y = - 3{x^4} + 4{x^2} + sqrt 2 ) trên đoạn (left[ { - 1;1} right]). c) (y = x + frac{{sqrt 5 }}{x}) trên đoạn (left[ {1;10} right]). d) (y = sin 2x - x) trên đoạn (left[ { - frac{pi }{2};frac{pi }{2}} right]).
Đề bài
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\).
b) \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\).
c) \(y = x + \frac{{\sqrt 5 }}{x}\) trên đoạn \(\left[ {1;10} \right]\).
d) \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về các cú pháp lệnh trong GeoGebra để thực hiện:

Lời giải chi tiết
a) Để tìm giá trị lớn nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\) ta nhập Max (<\({x^3} - 3{x^2} - 9x + 35\)>,,)

Vậy giá trị lớn nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\) là 40.
Để tìm giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\) ta nhập Min (<\({x^3} - 3{x^2} - 9x + 35\)>,,)
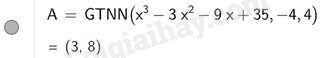
Vậy giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\) là 8.
b) Để tìm giá trị lớn nhất của hàm số \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\) ta nhập Max (<\( - 3{x^4} + 4{x^2} + \sqrt 2 \)>,,)
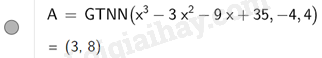
Vậy giá trị lớn nhất của hàm số \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\) là 40.
Để tìm giá trị nhỏ nhất của hàm số \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\) ta nhập Min (<\( - 3{x^4} + 4{x^2} + \sqrt 2 \)>,,)
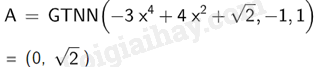
Vậy giá trị nhỏ nhất của hàm số \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\) là \(\sqrt 2 \).
c) Để tìm giá trị lớn nhất của hàm số \(y = x + \frac{{\sqrt 5 }}{x}\) trên đoạn \(\left[ {1;10} \right]\) ta nhập Max (<\(x + \frac{{\sqrt 5 }}{x}\)>,,)

Vậy giá trị lớn nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ {1;10} \right]\) là \(10 + \frac{{\sqrt 5 }}{{10}}\).
Để tìm giá trị nhỏ nhất của hàm số \(y = x + \frac{{\sqrt 5 }}{x}\) trên đoạn \(\left[ {1;10} \right]\) ta nhập Min (<\(x + \frac{{\sqrt 5 }}{x}\)>,,)

Vậy giá trị nhỏ nhất của hàm số \(y = x + \frac{{\sqrt 5 }}{x}\) trên đoạn \(\left[ {1;10} \right]\) là \(2\sqrt[4]{5}\).
d) Để tìm giá trị lớn nhất của hàm số \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) ta nhập Max (<\(\sin 2x - x\)>, <\( - \frac{\pi }{2}\)>, <\(\frac{\pi }{2}\)>)
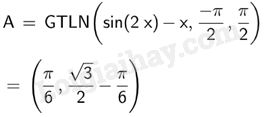
Vậy giá trị lớn nhất của hàm số \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \(\frac{{\sqrt 3 }}{2} - \frac{\pi }{6}\).
Để tìm giá trị nhỏ nhất của hàm số \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) ta nhập Min (<\(\sin 2x - x\)>, <\( - \frac{\pi }{2}\)>, <\(\frac{\pi }{2}\)>)
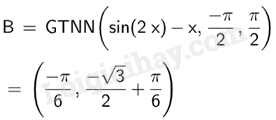
Vậy giá trị nhỏ nhất của hàm số \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{{\sqrt 3 }}{2} + \frac{\pi }{6}\).
Luyện Bài Tập Trắc nghiệm Toán 12 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 54 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 41 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 29 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 12 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 4 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 54 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 41 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 29 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 12 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 4 SGK Toán 12 tập 2 - Kết nối tri thức











Danh sách bình luận