 SBT Toán 11 - giải SBT Toán 11 - Cánh diều
SBT Toán 11 - giải SBT Toán 11 - Cánh diều
 Bài 1. Các số đặc trưng đo xu thế trung tâm cho mẫu số ..
Bài 1. Các số đặc trưng đo xu thế trung tâm cho mẫu số ..
Giải bài 3 trang 9 sách bài tập toán 11 - Cánh diều
Cho mẫu số liệu ghép nhóm thống kê thời gian sử dụng điện thoại trước khi ngủ
Đề bài
Cho mẫu số liệu ghép nhóm thống kê thời gian sử dụng điện thoại trước khi ngủ (đơn vị: phút) của một người trong 120 ngày như ở Bảng 8. Xác định các số đặc trưng đo xu thế trung tâm cho mẫu số liệu đó (làm tròn các kết quả đến hàng phần mười).
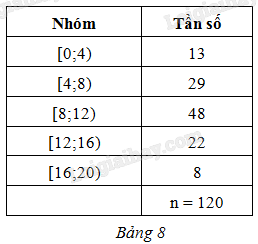
Phương pháp giải - Xem chi tiết
Áp dụng các công thức đã học để xác định các đại lượng tiêu biểu.
Lời giải chi tiết
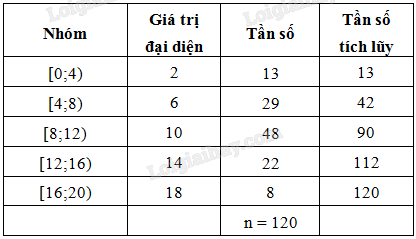
- Thời gian sử dụng điện thoại trung bình trước khi ngủ của một người trong 120 ngày là:
\(\bar x = \frac{{2.13 + 6.29 + 10.48 + 14.22 + 18.8}}{{120}} \approx 9,4\) (phút).
- Ta có: \(\frac{n}{2} = \frac{{120}}{2} = 60\) mà \(42 < 60 < 90.\) Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 60.
Xét nhóm 3 là nhóm [8;12) có \(r = 8,{\rm{ }}d = 4,{\rm{ }}{n_3} = 48\) và nhóm 2 là nhóm [4;8) có \(c{f_2} = 42.\)
Trung vị của mẫu số liệu là:
\({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 8 + \left( {\frac{{60 - 42}}{{48}}} \right).4 = 9,5\) (phút).
Tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = {M_e} = 9,5\) (phút).
- Ta có: \(\frac{n}{4} = \frac{{120}}{4} = 30\) mà \(13 < 30 < 42.\) Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 2 là nhóm [4;8) có \(s = 4,{\rm{ }}h = 4,{\rm{ }}{n_2} = 29\) và nhóm 1 là nhóm [0;4) có \(c{f_1} = 13.\)
Tứ phân vị thứ nhất của mẫu số liệu là:
\({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 4 + \left( {\frac{{30 - 13}}{{29}}} \right).4 \approx 6,3\) (phút).
- Ta có: \(\frac{{3n}}{4} = \frac{{3.120}}{4} = 90\) mà \(90 = 90 < 112.\) Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 90.
Xét nhóm 4 là nhóm [12;16) có \(t = 12,{\rm{ }}l = 2,{\rm{ }}{n_4} = 22\) và nhóm 3 là nhóm [8;12) có \(c{f_3} = 90.\)
Tứ phân vị thứ ba của mẫu số liệu là:
\({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l = 12 + \left( {\frac{{90 - 90}}{{22}}} \right).4 = 12\)(phút).
- Ta thấy: Nhóm 3 ứng với nửa khoảng [8;12) là nhóm có tần số lớn nhất với \(u = 8,{\rm{ }}g = 4,{\rm{ }}{n_3} = 48,{\rm{ }}{n_2} = 29,{\rm{ }}{n_4} = 22.\)
Mốt của mẫu số liệu là:
\({M_0} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 8 + \left( {\frac{{48 - 29}}{{2.48 - 29 - 22}}} \right).4 \approx 9,7\) (phút).
Các bài khác cùng chuyên mục












Danh sách bình luận