SBT Toán 11 - giải SBT Toán 11 - Chân trời sáng tạo Bài 5. Góc giữa đường thẳng và mặt phẳng Góc nhị diện -..

Giải bài 3 trang 73 sách bài tập toán 11 - Chân trời sáng tạo tập 2


Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng \(\frac{{a\sqrt {15} }}{6}\). Tính số đo góc phẳng nhị diện \(\left[ {S,BC,A} \right]\).

Đã có lời giải SGK Toán lớp 12 - Chân trời sáng tạo (mới)

Đầy đủ - Chi tiết - Chính xác

Đề bài

Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng \(\frac{{a\sqrt {15} }}{6}\). Tính số đo góc phẳng nhị diện \(\left[ {S,BC,A} \right]\).

Phương pháp giải - Xem chi tiết

+ Sử dụng kiến thức về góc nhị diện: Cho hai nửa mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{Q_1}} \right)\) có chung bờ là đường thẳng d. Hình tạo bởi \(\left( {{P_1}} \right)\), \(\left( {{Q_1}} \right)\) và d được gọi là góc nhị diện tạo bởi \(\left( {{P_1}} \right)\) và \(\left( {{Q_1}} \right)\), kí hiệu \(\left[ {{P_1},d,{Q_1}} \right]\).

+ Sử dụng kiến thức về góc phẳng nhị diện để tính: Góc phẳng nhị diện của góc nhị diện có đỉnh nằm trên cạnh của nhị diện, có hai cạnh lần lượt nằm trên hai mặt của nhị diện và vuông góc với cạnh của nhị diện.

Lời giải chi tiết

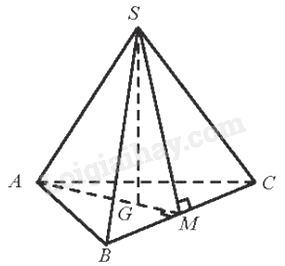
Gọi M là trung điểm của BC, G là trọng tâm của tam giác ABC.

Suy ra, \(SG \bot \left( {ABC} \right),SM \bot BC,AM \bot BC\)

Do đó, góc SMG là góc phẳng nhị diện \(\left[ {S,BC,A} \right]\)

Vì tam giác ABC đều cạnh a nên \(\widehat {ABC} \) \( = {60^0},AB \) \( = a\), AM là đường trung tuyến đồng thời là đường cao. Do đó, tam giác ABM vuông tại M. Suy ra: \(AM \) \( = AB.\sin {60^0} \) \( = \frac{{a\sqrt 3 }}{2}\)

Vì G là trọng tâm tam giác ABC nên \(GM \) \( = \frac{1}{3}AM \) \( = \frac{{a\sqrt 3 }}{6}\)

Vì tam giác SBC đều nên SM là đường trung tuyến đồng thời là đường cao.

Áp dụng định lí Pythagore vào tam giác SBM vuông tại G ta có:

\(SM \) \( = \sqrt {S{B^2} - B{M^2}}  \) \( = \frac{{a\sqrt 6 }}{6}\)

Vì \(SG \bot \left( {ABC} \right) \) \( \Rightarrow SG \bot GM\). Áp dụng định lí Pythagore vào tam giác SGM vuông tại G ta có: \(SG \) \( = \sqrt {S{M^2} - G{M^2}}  \) \( = \frac{{a\sqrt 3 }}{6}\)

Vì \(GM \) \( = SG\left( { = \frac{{a\sqrt 3 }}{6}} \right),\widehat {SGM} \) \( = {90^0}\) nên tam giác SMG vuông cân tại G.

Do đó, \(\widehat {SMG} \) \( = {45^0}\)


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua