-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
Giải bài 29 trang 114 sách bài tập toán 9 - Cánh diều tập 2
Cho lục giác đều ABCDEF với tâm O thoả mãn phép quay thuận chiều 60° tâm O biến các điểm A, B, C, D, E, F lần lượt thành các điểm B, C, D, E, F, A. Các điểm M, N lần lượt là trung điểm của EF, BD. a) Tìm α (0 < α < 180), biết phép quay ngược chiều α° tâm O biến các điểm D, C lần lượt thành các điểm B, A. b) Chứng minh phép quay thuận chiều 60° tâm A biến các điểm O, N lần lượt thành các điểm F, M.
Đề bài
Cho lục giác đều ABCDEF với tâm O thoả mãn phép quay thuận chiều 60° tâm O biến các điểm A, B, C, D, E, F lần lượt thành các điểm B, C, D, E, F, A. Các điểm M, N lần lượt là trung điểm của EF, BD.
a) Tìm α (0 < α < 180), biết phép quay ngược chiều α° tâm O biến các điểm D, C lần lượt thành các điểm B, A.
b) Chứng minh phép quay thuận chiều 60° tâm A biến các điểm O, N lần lượt thành các điểm F, M.
Phương pháp giải - Xem chi tiết
Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo \({\alpha ^o}\).
Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O được phát biểu tương tự như trên.
Lời giải chi tiết
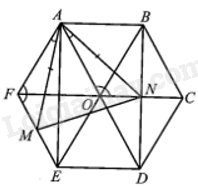
a) Do ABCDEF là lục giác đều có tâm O nên OA= OB = OC = OD = OE = OF.
Do phép quay thuận chiều 60° tâm O biến các điểm A, B, C lần lượt thành các điểm B, C, D nên \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = {60^o}\);
Do đó \(\widehat {DOB} = \widehat {DOC} = \widehat {COB} = {60^o} + {60^o} = {120^o}\)
\(\widehat {COA} = \widehat {COB} = \widehat {BOA} = {60^o} + {60^o} = {120^o}\).
Như vậy, phép quay ngược chiều 120° tâm O biến các điểm D, C lần lượt thành các điểm B, A.
b) Xét lục giác ABCDEF có tổng số đo các góc bằng tổng số đo hai tứ giác ABCD và ADEF, và bằng 2.360° = 720°.
Do ABCDEF là lục giác đều nên các góc của hình lục giác bằng nhau, và bằng
\(\frac{{{{720}^o}}}{6} = {120^o}\).
Xét ∆OAF có OA = OF và \(\widehat {AOF} = {60^o}\) nên ∆OAF là tam giác đều, suy ra AF = AO và \(\widehat {OAF} = {60^o}\).
Như vậy, phép quay thuận chiều 60° tâm A biến điểm O thành điểm F.
Xét ∆OBC có OB = OC và \(\widehat {BOC} = {60^o}\) nên ∆OBC là tam giác đều, do đó OB = OC = BC.
Chứng minh tương tự, ta sẽ có OB = BC = CD = OD nên tứ giác OBCD là hình thoi, do đó hai đường chéo OC và BD vuông góc với nhau tại trung điểm của mỗi đường.
Theo bài, N là trung điểm của BC nên N là trung điểm của OC, do đó OC = 2ON.
Ta có: M là trung điểm của EF nên EF = 2FM, mà EF = BC = OC nên OC = 2FM.
Suy ra FM = ON.
Xét ∆AFM và ∆AON có:
FA = AO, \(\widehat {AFM} = \widehat {AON} = {120^o}\), FM = ON
Do đó ∆AFM = ∆AON (c.g.c).
Suy ra AM = AN và \(\widehat {FAM} = \widehat {OAN}\).
Do đó, \(\widehat {MAN} = \widehat {MAO} + \widehat {OAN} = \widehat {MAO} + \widehat {MAF} \)
\(= \widehat {FAO} = {60^o}\).
Có AM = AN và \(\widehat {MAN} = {60^o}\) nên phép quay thuận chiều 60° tâm A biến điểm N thành điểm M.
Bình luận
Chia sẻ
- Giải bài 30 trang 115 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 31 trang 115 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 32 trang 115 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 28 trang 114 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 27 trang 114 sách bài tập toán 9 - Cánh diều tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
