Giải bài 24 trang 113 sách bài tập toán 9 - Cánh diều tập 2

Trên mặt phẳng toạ độ Oxy cho A(–2; –2). Phép quay thuận chiều 90° tâm O biến điểm A thành điểm I. Khi đó tọa độ của điểm I là: A. (–2; 0). B. (0; –2). C. (2; –2). D. (–2; 2).

Đề bài

Trên mặt phẳng toạ độ Oxy cho A(–2; –2). Phép quay thuận chiều 90° tâm O biến điểm A thành điểm I. Khi đó tọa độ của điểm I là:

A. (–2; 0).

B. (0; –2).

C. (2; –2).

D. (–2; 2).

Phương pháp giải - Xem chi tiết

Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo \({\alpha ^o}\).

Lời giải chi tiết

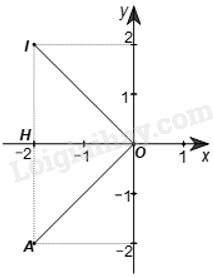
Gọi H là hình chiếu của A trên Ox. Ta có A(–2; –2) nên OH = AH = |–2| = 2.

Do đó ∆AOH vuông cân tại H, nên \(\widehat {AOH} = {45^o}\).

Xét ∆AOH vuông tại H, ta có: OA² = OH² + AH² (định lí Pythagore).

Suy ra \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {{2^2} + {2^2}} = \sqrt 8 = 2\sqrt 2 \).

Gọi I là điểm đối xứng với A qua Ox, do đó I(–2; 2). Ta cũng chứng minh được
\(\widehat {HOI} = {45^o}\) và OI = \(2\sqrt 2 \).

Như vậy, Phép quay thuận chiều 90° tâm O biến điểm A(–2; –2) thành điểm I(–2; 2).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 25 trang 114 sách bài tập toán 9 - Cánh diều tập 2
Quan sát các đa giác ở Hình 23 và cho biết hình nào là đa giác đều.
Giải bài 26 trang 114 sách bài tập toán 9 - Cánh diều tập 2
Cho ngũ giác đều ABCDE. Về phía ngoài của ngũ giác đó dựng tam giác đều PDE (Hình 24). Tính số đo góc APC.
Giải bài 27 trang 114 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác đều ABC có các đường cao AD, BE, CF cắt nhau tại H. Gọi I, K, M theo thứ tự là trung điểm của HA, HB, HC. Chứng minh lục giác DKFIEM là lục giác đều.
Giải bài 28 trang 114 sách bài tập toán 9 - Cánh diều tập 2
Cho lục giác đều ABCDEF. Về phía ngoài lục giác dựng các hình vuông BAA1A2, CBA3A4, DCA5A6, EDA7A8, FEA9A10, AFA11A12. Đa giác A1A2A3…A11A12 có phải là đa giác đều không? Vì sao?
Giải bài 29 trang 114 sách bài tập toán 9 - Cánh diều tập 2
Cho lục giác đều ABCDEF với tâm O thoả mãn phép quay thuận chiều 60° tâm O biến các điểm A, B, C, D, E, F lần lượt thành các điểm B, C, D, E, F, A. Các điểm M, N lần lượt là trung điểm của EF, BD. a) Tìm α (0 < α < 180), biết phép quay ngược chiều α° tâm O biến các điểm D, C lần lượt thành các điểm B, A. b) Chứng minh phép quay thuận chiều 60° tâm A biến các điểm O, N lần lượt thành các điểm F, M.
Giải bài 30 trang 115 sách bài tập toán 9 - Cánh diều tập 2
Trên mặt phẳng tọa độ Oxy cho hình vuông ABCD với A(0; 2), B(–2; 0), C(0; –2), D(2; 0). Phép quay thuận chiều 90° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Tính chu vi tứ giác A’B’C’D’.
Giải bài 31 trang 115 sách bài tập toán 9 - Cánh diều tập 2
Cho hình vuông ABCD và O là giao điểm của AC và BD. Gọi M là trung điểm của AB, N là trung điểm của AO (Hình 25). Phép quay ngược chiều 90° tâm O biến các điểm N, M lần lượt thành các điểm N’, M’. a) Chứng minh tam giác BN'M' là tam giác vuông cân. b) Tính tỉ số diện tích tam giác ANM và diện tích tam giác CN'M'. c) Phát biểu “Phép quay thuận chiều 90° tâm N biến điểm O thành điểm M, biến điểm D thành điểm B” là đúng hay sai? Vì sao?
Giải bài 32 trang 115 sách bài tập toán 9 - Cánh diều tập 2
Quan sát bề mặt của chiếc diều, khung cửa sổ, chiếc bàn như ở các hình 26a, 26b, 26c. Các bề mặt của mỗi vật thể đó có dạng hình đa giác đều hay không?
Giải bài 23 trang 113 sách bài tập toán 9 - Cánh diều tập 2
Tổng số đo tất cả các góc của ngũ giác ABCDE là: A. 560°. B. 540°. C. 520°. D. 500°.