Giải bài 22 trang 88 sách bài tập toán 9 - Cánh diều tập 1

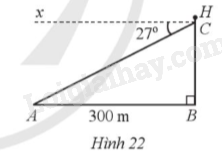
Trên mặt biển, khi khoảng cách từ ca nô đến chân tháp hải đăng là AB = 300 m, một người đứng trên tháp hải đăng đó, đặt mắt tại vị trí C và nhìn về phía ca nô theo phương CA tạo với phương nằm ngang Cx một góc là \(\widehat {ACx} = 27^\circ \) (minh hoạ ở Hình 22). Tính chiều cao BH của tháp hải đăng (làm tròn kết quả đến hàng phần trăm của mét), biết AB//Cx và độ cao từ tầm mắt của người đó đến đỉnh tháp hải đăng là CH = 2,1 m.

Đề bài

Trên mặt biển, khi khoảng cách từ ca nô đến chân tháp hải đăng là AB = 300 m, một người đứng trên tháp hải đăng đó, đặt mắt tại vị trí C và nhìn về phía ca nô theo phương CA tạo với phương nằm ngang Cx một góc là \(\widehat {ACx} = 27^\circ \) (minh hoạ ở Hình 22). Tính chiều cao BH của tháp hải đăng (làm tròn kết quả đến hàng phần trăm của mét), biết AB//Cx và độ cao từ tầm mắt của người đó đến đỉnh tháp hải đăng là CH = 2,1 m.

Phương pháp giải - Xem chi tiết

Bước 1: Tính BC (dựa vào tỉ số lượng giác trong tam giác ABC).

Bước 2: \(BH = BC + CH\).

Lời giải chi tiết

Do AB//Cx nên \(\widehat {BAC} = \widehat {ACx} = 27^\circ \) (so le trong).

Ta lại có tam giác ABC vuông tại C nên \(\tan A = \frac{{BC}}{{AB}}\) hay \(BC = AB.\tan A = 300.\tan 27^\circ \).

Chiều cao BH của tháp hải đăng là:

\(BH = BC + CH = 300.\tan 27^\circ + 2,1 \approx 154,96\)m.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 23 trang 88 sách bài tập toán 9 - Cánh diều tập 1
Một thuyền đi với tốc độ 20km/h theo hướng Đông trong 1 giờ 30 phút từ vị trí P đến vị trí A. Sau đó nó sẽ đi theo hướng Bắc với cùng tốc độ trong 3 giờ 30 phút đến vị trí B (Hình 23). Tính góc so với hướng Đông mà thuyền đi từ vị trí P đến vị trí B (làm tròn kết quả đến hàng đơn vị của phút).
Giải bài 24 trang 89 sách bài tập toán 9 - Cánh diều tập 1
Từ một máy bay trực thăng, một người đặt mắt tại vị trí M ở độ cao MH = 920 m. Người đó nhìn hai vị trí A và B của hai đầu một cây cầu theo phương MA và MB tạo với phương nằm ngang Mx các góc lần lượt là \(\widehat {AMx} = 37^\circ ,\widehat {BMx} = 31^\circ \)với Mx // AB (Hình 24). Hỏi độ dài AB của cây cầu là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Giải bài 25 trang 89 sách bài tập toán 9 - Cánh diều tập 1
Từ một đài quan sát, một người đặt mắt tại vị trí B. Người đó nhìn thấy một chiếc ô tô ở vị trí C theo phương BC tạo với phương nằm ngang Bx một góc là \(\widehat {CBx} = 23^\circ \)với Bx // AC. Khi đó, khoảng cách giữa ô tô và chân đài quan sát là AC = 1284 m. Nếu ô tô từ vị trí C tiếp tục đi về phía chân đài quan sát với tốc độ 60 km/h thì sau 1 phút, người đó nhìn thấy ô tô ở vị trí D với góc \(\widehat {DBx} = \alpha ^\circ \) (Hình 25).a) Tính chiều cao của đài quan sát (làm tròn kết quả đ
Giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1
Flycam là từ viết tắt của Fly camera. Đây là thiết bị bay không người lái có lắp camera hay máy ảnh để quay phim hoặc chụp ảnh từ trên cao. Một chiếc Flycam đang ở vị trí A cách cây cầu BC (theo phương thẳng đứng) một khoảng AH = 120m. Biết góc tạo bởi phương AB, AC với các phương vuông góc với mặt cầu tại B, C lần lượt là \(\widehat {ABx} = 30^\circ ,\widehat {ACx} = 45^\circ \) (hình 26). Tính độ dài BC của cây cầu (làm tròn kết quả đến hàng phần trăm của mét).
Giải bài 21 trang 88 sách bài tập toán 9 - Cánh diều tập 1
Bạn Hoa vẽ mặt cắt đứng phần mái của một ngôi nhà có dạng tam giác cân ABC (mái hai dốc). Biết rằng góc tạo bởi phần mái nhà và mặt phẳng nằm ngang là \(\widehat {ABC} = 25^\circ \) và độ dài mỗi bên dốc mái là 3,5m (hình 21). Tính độ dài đoạn thẳng BC (làm tròn kết quả đến hàng phần mười của mét).
Giải bài 20 trang 88 sách bài tập toán 9 - Cánh diều tập 1
Một người đứng chào cờ (ở vị trí A) cách cột cờ (ở vị trí C) với AC = 20 m. Người đó đặt mắt tại vị trí B cách mặt đất một khoảng là AB = 1,5 m. Người đó nhìn lên đỉnh cột cờ (ở vị trí E) theo phương BE tạo với phương nằm ngang BD một góc là \(\widehat {EBD} = 32^\circ \) (Hình 20). Tính chiều cao của cột cờ (làm tròn kết quả đến hàng đơn vị của mét).
Giải bài 19 trang 87 sách bài tập toán 9 - Cánh diều tập 1
Một khối u (ở vị trí A) của một bệnh nhân cách da mặt 5,7 cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia (ở vị trí B) cách hình chiếu của khối u (ở vị trí C) trên da mặt là 8,3 cm (Hình 19). a) Hỏi góc tạo bởi chùm tia gamma với da mặt là bao nhiêu độ (làm tròn kết quả đến hàng phần mười)? b) Chùm tia phải đi một đoạn dài bao nhiêu centimét để đến được khối u (làm tròn kết quả đến hàng phần mười).
Giải bài 18 trang 87 sách bài tập toán 9 - Cánh diều tập 1
Tính chiều cao của cột cờ (làm tròn kết quả đến hàng phần trăm của mét), biết bóng của cột cờ được chiếu bởi ánh sáng Mặt Trời xuống mặt đất dài 10,5 m và góc tạo bởi tia sáng với phương nằm ngang là 36°.