SBT Toán 12 - Giải SBT Toán 12 - Kết nối tri thức Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liê..

Giải bài 1.49 trang 32 sách bài tập toán 12 - Kết nối tri thức


a) Nếu \(C\left( x \right)\) (USD) là chi phí sản xuất \(x\) đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\). Chứng minh rằng nếu chi phí trung bình là nhỏ nhất thì chi phí biên bằng chi phí trung bình. b) Nếu \(C\left( x \right) = 16000 + 200x + 4{x^{\frac{3}{2}}}\), hãy tìm: (i) Chi phí, chi phí trung bình và chi phí biên khi sản xuất \(100\) đơn vị hàng hóa; (ii) Mức sản xuất mà khi đó sẽ giảm thiểu chi phí trung bì

Đề bài

a) Nếu \(C\left( x \right)\) (USD) là chi phí sản xuất \(x\) đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\). Chứng minh rằng nếu chi phí trung bình là nhỏ nhất thì chi phí biên bằng chi phí trung bình.

b) Nếu \(C\left( x \right) = 16000 + 200x + 4{x^{\frac{3}{2}}}\), hãy tìm:

(i) Chi phí, chi phí trung bình và chi phí biên khi sản xuất \(100\) đơn vị hàng hóa;

(ii) Mức sản xuất mà khi đó sẽ giảm thiểu chi phí trung bình;

(iii) Chi phí trung bình nhỏ nhất.

Phương pháp giải - Xem chi tiết

Ý a: Tính \(\overline {C'} \left( x \right)\), sử dụng ý nghĩa của cực tiểu để chứng minh.

Ý b: Xác định công thức các hàm \(\overline C \left( x \right)\), \(C'\left( x \right)\).

(i) Thay \(x = 100\) vào các hàm  \(C\left( x \right)\), \(\overline C \left( x \right)\), \(C'\left( x \right)\).

(ii) Khảo sát sự biến thiên của hàm \(\overline C \left( x \right)\), xác định khoảng mà hàm nghịch biến từ đó ruy ra mức sản xuất x.

(iii) Tìm giá trị nhỏ nhất của hàm số \(\overline C \left( x \right)\).

Lời giải chi tiết

a) Ta có \(\overline {C'} \left( x \right) = {\left[ {\frac{{C\left( x \right)}}{x}} \right]^\prime } = \frac{{C'\left( x \right) \cdot x - C\left( x \right)}}{{{x^2}}}\).

Chi phí trung bình nhỏ nhất khi \(\overline {C'} \left( x \right) = 0\) hay \(C'\left( x \right) \cdot x - C\left( x \right) = 0 \Leftrightarrow C'\left( x \right) = \frac{{C\left( x \right)}}{x}\).

Nói cách khác chi phí biên bằng chi phí trung bình.

b) Xét hàm số \(C\left( x \right) = 16000 + 200x + 4{x^{\frac{3}{2}}}\).

Ta có hàm chi phí trung bình là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{16000 + 200x + 4{x^{\frac{3}{2}}}}}{x} = \frac{{16000}}{x} + 200 + 4{x^{\frac{1}{2}}}\).

Hàm chi phí biên là \(C'\left( x \right) = 200 + 6{x^{\frac{1}{2}}}\).

(i) Ta có \(C\left( {100} \right) = 16000 + 200 \cdot 100 + 4 \cdot {100^{\frac{3}{2}}} = 40000\); \(\overline C \left( {100} \right) = \frac{{16000}}{{100}} + 200 + 4 \cdot {100^{\frac{1}{2}}} = 400\);

\(C'\left( {100} \right) = 200 + 6 \cdot {100^{\frac{1}{2}}} = 260\).

Vậy chi phí, chi phí trung bình và chi phí biên ở mức sản xuất 100 đơn vị hàng hóa lần lượt là \(40000\) USD, \(400\) USD và \(260\) USD.

(ii) Ta có \(\overline {C'} \left( x \right) = \frac{{ - 16000}}{{{x^2}}} + 2{x^{ - \frac{1}{2}}}\) khi đó \(\overline {C'} \left( x \right) = 0 \Leftrightarrow \frac{{ - 16000}}{{{x^2}}} + 2{x^{ - \frac{1}{2}}} = 0 \Leftrightarrow x = 400\) do \(x > 0\).

Lập bảng biến thiên

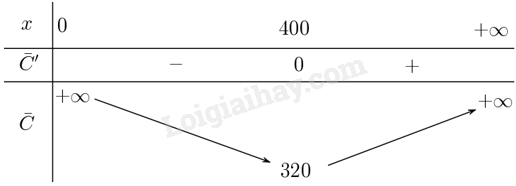
Từ bảng biến thiên suy ra, mức sản xuất là 400 đơn vị hàng hóa thì sẽ giảm thiểu giá trị trung bình.

(iii)  Chi phí trung bình nhỏ nhất là 320 USD.


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải bài 1.50 trang 33 sách bài tập toán 12 - Kết nối tri thức

    a) Chứng tỏ rằng nếu lợi nhuận (Pleft( x right)) là cực đại thì doanh thu biên bằng chi phí biên. b) Cho (Cleft( x right) = 16000 + 500x - 1,6{x^2} + 0,004{x^3}) là hàm chi phí và (pleft( x right) = 1700 - 7x) là hàm cầu. Hãy tìm mức sản xuất sẽ tối đa lợi nhuận.

  • Giải bài 1.48 trang 32 sách bài tập toán 12 - Kết nối tri thức

    Một công ty ước tính rằng chi phí (C) (USD) để sản xuất (x) đơn vị sản phẩm có thể được mô hình hóa bằng công thức (C = 800 + 0,04x + 0,0002{x^2}). Tìm mức sản xuất sao cho chi phí trung bình (overline C left( x right) = frac{{Cleft( x right)}}{x}) cho mỗi đơn vị hàng hóa là nhỏ nhất.

  • Giải bài 1.47 trang 32 sách bài tập toán 12 - Kết nối tri thức

    Doanh thu (R) (USD) từ vệc cho thuê (x) căn hộ có thể được mô hình hóa bằng hàm số (R = 2xleft( {900 + 32x - {x^2}} right)). a) Tìm hàm doanh thu biên. b) Tìm doanh thu biên khi (x = 14) và giải thích ý nghĩa thực tiễn của nó. c) Tìm lượng doanh thu tăng thêm khi số căn hộ cho thuê tăng từ (14) lên (15).

  • Giải bài 1.46 trang 32 sách bài tập toán 12 - Kết nối tri thức

    Ở ({0^ circ }C), sự mất nhiệt (H) (tính bằng Kcal/m2h, ở đây Kcal là kilocalories và 1 Kcal=1000 calo) từ cơ thể của một người có thể được mô hình hóa bằng công thức (H = 33left( {10sqrt v - v + 10,45} right),) Trong đó (v) là tốc độ gió (tính bằng m/s) (Theo sách Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009). a) Xét tính đơn điệu của hàm số (H) và giải thích ý nghĩa thực tiễn của kết quả nhận được. b) Tìm tốc độ thay đổi của (H) khi (v = 2) m/

  • Giải bài 1.45 trang 32 sách bài tập toán 12 - Kết nối tri thức

    Chứng tỏ rẳng một thùng hình trụ có thể tích (V) cố định cần ít vật liệu sản xuất nhất (tức là có diện tích bề mặt nhỏ nhất) khi chiều cao của thùng gấp đôi bán kính đáy.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store