Giải bài 14 trang 90 sách bài tập toán 9 - Cánh diều tập 2
Chứng minh rằng trong một đường tròn, hai dây không đi qua tâm không thể cắt nhau tại trung điểm mỗi đường.
Đề bài
Chứng minh rằng trong một đường tròn, hai dây không đi qua tâm không thể cắt nhau tại trung điểm mỗi đường.
Phương pháp giải - Xem chi tiết
Chứng minh ngược lại: Giả sử có hai dây không đi qua tâm không thể cắt nhau tại trung điểm mỗi đường. Sau đó chứng minh giả sử là sai.
Lời giải chi tiết
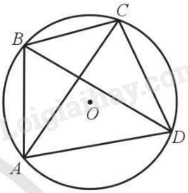
Giả sử trái lại có hai dây cung BD và AC (không đi qua tâm O) cắt nhau tại trung điểm mỗi đường.
Suy ra tứ giác ABCD là hình bình hành.
Do đó \(\widehat {ABC} = \widehat {ADC}\).
Mặt khác, tứ giác ABCD nội tiếp nên \(\widehat {ABC} + \widehat {ADC} = {180^o}\).
Suy ra \(\widehat {ABC} = \widehat {ADC} = {90^o}\), từ đó suy ra AC là đường kính của đường tròn (O) hay AC đi qua tâm O, mâu thuẫn với điều giả sử.
Vậy trong một đường tròn, hai dây không đi qua tâm không thể cắt nhau tại trung điểm mỗi đường.
- Giải bài 15 trang 90 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 16 trang 90 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 17 trang 90 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 18 trang 91 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 19 trang 91 sách bài tập toán 9 - Cánh diều tập 2
>> Xem thêm
Các bài khác cùng chuyên mục













Danh sách bình luận