Giải bài 13 trang 92 sách bài tập toán 8 - Cánh diều

Cho hình thang cân (ABCD) có (AB//CD,AB = 3mc,CD = 6cm,AD = 2.5cm). Gọi (M,N) lần lượt là hình chiếu của (A,B) trên đường thẳng (CD).

Đề bài

Cho hình thang cân \(ABCD\) có \(AB//CD,AB = 3mc,CD = 6cm,AD = 2.5cm\). Gọi \(M,N\) lần lượt là hình chiếu của \(A,B\) trên đường thẳng \(CD\). Tính độ dài các đoạn thẳng \(DM,DN,AM\).

Phương pháp giải - Xem chi tiết

Áp dụng các trường hợp bằng nhau của tam giác vuông và tính chất của hình thang cân để tính độ dài các đoạn thẳng \(DM,DN,AM\).

Lời giải chi tiết

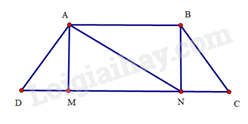
Xét tam giác ADM và tam giác ACM có:

AD = BC (vì ABCD là hình thang cân)

\(\widehat{D} = \widehat{C}\) (vì ABCD là hình thang cân)

Suy ra \(\Delta ADM = \Delta BCN\) (cạnh huyền – góc nhọn)

Do đó \(AM = BN;DM = CN\)

Xét tam giác ABN và tam giác NMA có:

AN chung

\(\widehat{BAN} = \widehat{MNA}\) (hai góc so le trong)

Suy ra \(\Delta ABN = \Delta NMA\) (cạnh huyền – góc nhọn)

nên \(AB = NM\). Do đó, \(NM = 3cm\)

Ta có: \(DM + NM + CN = CD\) và \(DM = CN\) nên \(2DM + 3 = 6\)

Suy ra \(DM = 1,5\)

Mà \(DN = DM + NM\), suy ra \(DN = 4,5cm\)

Trong tam giác \(ADM\) vuông tại \(M\), ta có:

\(A{D^2} = A{M^2} + D{M^2}\)

Suy ra \(A{M^2} = A{D^2} - D{M^2} = 4\).

Vậy \(AM = \sqrt 4 = 2\left( {cm} \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 14 trang 92 sách bài tập toán 8 - Cánh diều
Cho tam giác \(ABC\) cân tại \(A\). Lấy điểm \(M,N\) lần lượt trên cạnh \(AB,AC\) sao cho \(AM = AN\).
Giải bài 15 trang 92 sách bài tập toán 8 - Cánh diều
Cho tam giác đều \(ABC\) có độ dài cạnh là 6 cm. trên tia \(BA,CA\) lần lượt lấy điểm \(D,E\) sao cho \(AD = AE = 2cm\) (Hình 12)
Giải bài 12 trang 92 sách bài tập toán 8 - Cánh diều
Cho hình thang cân \(ABCD\) có \(AB//CD,AB < CD\), hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(P\), hai cạnh bên \(AD\) và \(BC\) kéo dài cắt nhau tại \(Q\).
Giải bài 11 trang 92 sách bài tập toán 8 - Cánh diều
Cho tứ giác \(ABCD\) có \(\widehat C = \widehat D\) và \(AD = BC\). Chứng minh tứ giác \(ABCD\) là hình thang cân.