Giải bài 10 trang 37 sách bài tập toán 9 - Cánh diều tập 1
Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn (frac{{AB.BC + AD.DC}}{2}.)
Đề bài
Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn \(\frac{{AB.BC + AD.DC}}{2}.\)
Phương pháp giải - Xem chi tiết
Kẻ đường cao CH và AK.
Tính diện tích tam giác ABC và ACD.
Do đó\({S_{ABCD}} = {S_{ABC}} + {S_{ACD}} = \frac{{AB.CH + DC.AK}}{2}\)
Kết hợp với điều kiện \(CH \le BC,AK \le AD\), ta được điều phải chứng minh.
Lời giải chi tiết
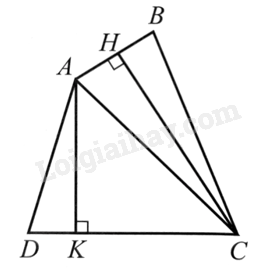
Kẻ \(CH \bot AB,AK \bot DC(H \in AB,K \in DC)\).
Ta có \({S_{ABC}} = \frac{{AB.CH}}{2},{S_{ACD}} = \frac{{DC.AK}}{2}\)
Do đó
\({S_{ABCD}} = {S_{ABC}} + {S_{ACD}} \\= \frac{{AB.CH}}{2} + \frac{{DC.AK}}{2} = \frac{{AB.CH + DC.AK}}{2}\)
Mà \(CH \le BC,AK \le AD\) suy ra \({S_{ABCD}} \le \frac{{AB.BC + AD.DC}}{2}\)
Vậy diện tích của tứ giác ABCD không lớn hơn \(\frac{{AB.BC + AD.DC}}{2}.\)
- Giải bài 11 trang 37 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 9 trang 36 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 8 trang 36 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 7 trang 36 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 6 trang 35 sách bài tập toán 9 - Cánh diều tập 1
>> Xem thêm
Các bài khác cùng chuyên mục













Danh sách bình luận