Giải bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Cho hình chữ nhật ABCD có AC cắt BD tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC

Tổng hợp đề thi giữa kì 1 lớp 11 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Cho hình chữ nhật ABCD có AC cắt BD tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hình thang JLKI và hình thang IHDC đồng dạng với nhau.

Phương pháp giải - Xem chi tiết

Dựa vào các phép biến hình đã học để làm

Lời giải chi tiết

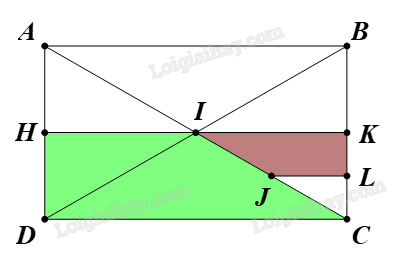
Ta có J là trung điểm IC (giả thiết).

Suy ra \(\overrightarrow {CI} = 2\overrightarrow {CJ} \)

Do đó \({V_{\left( {C,{\rm{ }}2} \right)}}\left( J \right){\rm{ }} = {\rm{ }}I.\)

Chứng minh tương tự, ta được \({V_{\left( {C,{\rm{ }}2} \right)}}\left( L \right){\rm{ }} = {\rm{ }}K,{\rm{ }}{V_{\left( {C,{\rm{ }}2} \right)}}\left( K \right){\rm{ }} = {\rm{ }}B,{\rm{ }}{V_{\left( {C,{\rm{ }}2} \right)}}\left( I \right){\rm{ }} = {\rm{ }}A.\)

Vì vậy \({V_{\left( {C,{\rm{ }}2} \right)}}\;\) biến hình thang JLKI thành hình thang IKBA.

Hình chữ nhật ABCD có I là giao điểm của hai đường chéo, suy ra I là trung điểm BD.

Do đó \({Đ_I}\left( B \right){\rm{ }} = {\rm{ }}D.\)

Chứng minh tương tự, ta được \({Đ_I}\left( A \right){\rm{ }} = {\rm{ }}C,{\rm{ }}{Đ_I}\left( K \right){\rm{ }} = {\rm{ }}H.\)

Lại có \({Đ_I}\left( I \right){\rm{ }} = {\rm{ }}I.\)

Do đó Đ_I biến hình thang IKBA thành hình thang IHDC.

Vì vậy phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm C, tỉ số 2 và phép đối xứng tâm I biến hình thang JLKI thành hình thang IHDC.

Vậy hình thang JLKI và hình thang IHDC đồng dạng với nhau.

👉

Giải bài nhanh với AI Hay: