Đề thi vào 10 môn Toán Vĩnh Phúc năm 2025
Tải vềCâu 1: (1 điểm) Trong một hộp kín đựng 10 tấm thẻ được đánh số tự nhiên từ 1 đến 10, không có hai thẻ nào được đánh số giống nhau. Lấy ngẫu nhiên một tấm thẻ từ trong hộp đã cho. Tính xác suất của biến cố A: "Lấy được thẻ ghi số chẵn".
Đề bài
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
Câu 1. Điều kiện xác định của biểu thức \(\sqrt {x + 2025} \) là
A. \(x \le - 2025\).
B. \(x < - 2025\).
C. \(x > - 2025\).
D. \(x \ge - 2025\).
Câu 2. Cặp số \(\left( {x;y} \right) = \left( {1;2} \right)\) là nghiệm của phương trình nào sau đây?
A. \(2x - 3y = 12\).
B. \(3x - y = 1\).
C. \(x + y = 5\).
D. \(x - 2y = 1\).
Câu 3. Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = - 1}\\{x + 4y = 3}\end{array}} \right.\)?
A. \(\left( { - 1;1} \right)\).
B. \(\left( {1;1} \right)\).
C. \(\left( {1; - 1} \right)\).
D. \(\left( {1;2} \right)\).
Câu 4. Cho phương trình bậc hai \({x^2}-5x + 6 = 0\) có hai nghiệm \({x_1},{x_2}\). Giá trị \({x_1} + {x_2}\) bằng
A. \( - 6\).
B. \( - 5\).
C. \(6\).
D. \(5\).
Câu 5. Thống kê điểm kiểm tra học kỳ 2 của lớp 9A thu được bảng như sau:

Theo bảng số liệu trên, lớp 9A có bao nhiêu học sinh đạt điểm 7?
A. 10.
B. 8.
C. 9.
D. 7.
Câu 6. Người ta thống kê lại chiều cao một loại cây sau một năm tuổi cho ở bảng ghép nhóm như sau:

Giá trị đại diện của nhóm \(\left[ {50;55} \right)\) bằng
A. 50.
B. 52,5.
C. 55.
D. 18.
Câu 7. Bóng của một cái cây do ánh nắng mặt trời chiếu xuống mặt đất dài 20 m. Biết rằng các tia sáng của ánh nắng mặt trời song song với nhau và tạo với mặt đất một góc \({45^ \circ }\) (tham khảo hình vẽ bên). Chiều cao của cái cây đó là
A. \(20\sqrt 2 \) m.
B. 10 m.
C. 20 m.
D. \(10\sqrt 2 \) m.
Câu 8. Cho khối trụ có bán kính đáy bằng 5 dm và chiều cao bằng 6 dm. Thể tích của khối trụ đó là
A. \(150\pi \) dm\(^3\).
B. \(30\pi \) dm\(^3\).
C. \(50\pi \) dm\(^3\).
D. \(60\pi \) dm\(^3\).
II. PHẦN TỰ LUẬN (8,0 điểm)
Câu 1: (1 điểm) Trong một hộp kín đựng 10 tấm thẻ được đánh số tự nhiên từ 1 đến 10, không có hai thẻ nào được đánh số giống nhau. Lấy ngẫu nhiên một tấm thẻ từ trong hộp đã cho. Tính xác suất của biến cố A: "Lấy được thẻ ghi số chẵn".
Câu 2: (1 điểm) Cho biểu thức \(P = \left( {\frac{1}{{\sqrt x + 1}} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x }}{{\sqrt x - 1}}\) (với điều kiện \(x > 0\), \(x \ne 1\)).
a) Rút gọn biểu thức \(P\).
b) Tìm tất cả các giá trị thực của \(x\) để \(23x.P = 2025\).
Câu 3: (1 điểm) Một cái cổng được thiết kế dạng parabol có phương trình biểu diễn trong hệ trục toạ độ Oxy là \(y = a{x^2}\) (với a là hằng số khác 0). Biết khoảng cách giữa hai chân cổng là AB = 6m, chiều cao từ điểm chính giữa cổng đến mặt đấy là OI = 4,5m (tham khảo hình vẽ sau).
a) Tìm hệ số a dựa vào dữ kiện đã cho.
b) Một xe tải có chiều rộng bằng 2m, chiều cao bằng 3,2m (tham khảo hình vẽ trên) đi vào chính giữa cổng trên. Hỏi xe tải này có thể đi qua được cổng đó mà không chạm vào cổng hay không? Giải thích lý do.
Câu 4: (1 điểm) Bác Vĩnh và bác Phúc cùng gửi tiền tiết kiệm vào ngân hàng với tổng số tiền là 900 triệu đồng. Bác Vĩnh gửi vào ngân hàng A với lãi suất 7% một năm, bác Phúc gửi vào ngân hàng B với lãi suất 6% một năm. Sau khi gửi được đúng một năm, tổng số tiền lãi mà hai bác nhận được là 60 triệu đồng. Hỏi ban đầu mỗi bác gửi tiết kiệm bao nhiêu tiền?
Câu 5: (3 điểm) Cho nửa đường tròn đường kính AB, có tâm là điểm O. Đường thẳng đi qua tâm O và vuông góc với đường kính AB cắt nửa đường tròn đã cho tại điểm C. Trên tia đối của tia CA lấy điểm D (D không trùng với C), kẻ CH vuông góc với đường thẳng BD tại điểm H.
a) Chứng minh tứ giác OBHC nội tiếp.
b) Gọi E là giao điểm của hai đường thẳng HO và BC. Chứng minh HO là tia phân giác của \(\angle CHB\) và \(CE \cdot CH = BE \cdot HD\).
c) Đường tròn ngoại tiếp tam giác CDH cắt nửa đường tròn đường kính AB tại điểm K (K không trùng với C). Chứng minh \(DE > 2.CK\).
Câu 6: (1 điểm) Cho \(a,{\mkern 1mu} b,{\mkern 1mu} c\) là các số thực dương thỏa mãn \(ab + 4bc + 4ca = 28\). Tìm giá trị nhỏ nhất của biểu thức \(T = \frac{{11a + 11b + 24c}}{{\sqrt {8{a^2} + 224} + \sqrt {8{b^2} + 224} + \sqrt {16{c^2} + 28} }}\).
-------- Hết --------
Lời giải
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
|
1.D |
2.B |
3.A |
4.D |
5.C |
6.B |
7.C |
8.A |
Câu 1. Điều kiện xác định của biểu thức \(\sqrt {x + 2025} \) là
A. \(x \le - 2025\).
B. \(x < - 2025\).
C. \(x > - 2025\).
D. \(x \ge - 2025\).
Phương pháp:
Điều kiện xác định của căn thức bậc hai \(\sqrt A \) là \(A \ge 0\).
Lời giải:
Điều kiện xác định của biểu thức \(\sqrt {x + 2025} \) là \(x + 2025 \ge 0\), suy ra \(x \ge - 2025\).
Đáp án: D
Câu 2. Cặp số \(\left( {x;y} \right) = \left( {1;2} \right)\) là nghiệm của phương trình nào sau đây?
A. \(2x - 3y = 12\).
B. \(3x - y = 1\).
C. \(x + y = 5\).
D. \(x - 2y = 1\).
Phương pháp:
Thay \(x = 1;y = 2\) vào các phương trình để tính.
Lời giải:
Thay \(x = 1;y = 2\) vào các phương trình, ta được:
\(\begin{array}{l}2.1 - 3.2 = - 4 \ne 12\\3.1 - 2 = 1\\1 + 2 = 3 \ne 5\\1 - 2.2 = - 3 \ne 1\end{array}\)
nên \(\left( {x;y} \right) = \left( {1;2} \right)\) là nghiệm của phương trình \(3x - y = 1\).
Đáp án: B
Câu 3. Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = - 1}\\{x + 4y = 3}\end{array}} \right.\)?
A. \(\left( { - 1;1} \right)\).
B. \(\left( {1;1} \right)\).
C. \(\left( {1; - 1} \right)\).
D. \(\left( {1;2} \right)\).
Phương pháp:
Đối với bài tập trắc nghiệm, sử dụng máy tính cầm tay để bấm nghiệm.
Lời giải:
Sử dụng máy tính cầm tay, ta tính được:\(\left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\).
Đáp án: A
Câu 4. Cho phương trình bậc hai \({x^2}-5x + 6 = 0\) có hai nghiệm \({x_1},{x_2}\). Giá trị \({x_1} + {x_2}\) bằng
A. \( - 6\).
B. \( - 5\).
C. \(6\).
D. \(5\).
Phương pháp:
Đối với bài tập trắc nghiệm, sử dụng máy tính cầm tay để bấm nghiệm.
Lời giải:
Sử dụng máy tính cầm tay, ta tính được phương trình có hai nghiệm \({x_1} = 3;{x_2} = 2\).
Suy ra \({x_1} + {x_2} = 3 + 2 = 5\).
Đáp án: D
Câu 5. Thống kê điểm kiểm tra học kỳ 2 của lớp 9A thu được bảng như sau:

Theo bảng số liệu trên, lớp 9A có bao nhiêu học sinh đạt điểm 7?
A. 10.
B. 8.
C. 9.
D. 7.
Phương pháp:
Quan sát bảng số liệu để xác định.
Lời giải:
Lớp 9A có 9 học sinh đạt điểm 7.
Đáp án: C
Câu 6. Người ta thống kê lại chiều cao một loại cây sau một năm tuổi cho ở bảng ghép nhóm như sau:

Giá trị đại diện của nhóm \(\left[ {50;55} \right)\) bằng
A. 50.
B. 52,5.
C. 55.
D. 18.
Phương pháp:
Giá trị đại diện của nhóm \({\rm{[}}a,b)\) là \(\frac{{a + b}}{2}\).
Lời giải:
Giá trị đại diện của nhóm \(\left[ {50;55} \right)\) bằng \(\frac{{50 + 55}}{2} = 52,5\).
Đáp án: B
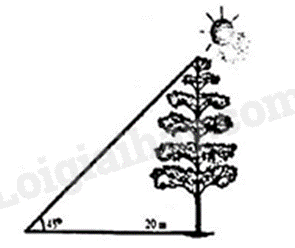
Câu 7. Bóng của một cái cây do ánh nắng mặt trời chiếu xuống mặt đất dài 20 m. Biết rằng các tia sáng của ánh nắng mặt trời song song với nhau và tạo với mặt đất một góc \(45^\circ \) (tham khảo hình vẽ bên). Chiều cao của cái cây đó là
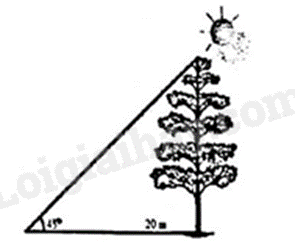
A. \(20\sqrt 2 \) m.
B. 10 m.
C. 20 m.
D. \(10\sqrt 2 \) m.
Phương pháp:
Xác định hệ thức lượng tương ứng rồi tính chiều cao cây.
Lời giải:
Chiều cao của cái cây đó là: \(20.\tan 45^\circ = 20\left( m \right)\)
Đáp án: C
Câu 8. Cho khối trụ có bán kính đáy bằng 5 dm và chiều cao bằng 6 dm. Thể tích của khối trụ đó là
A. \(150\pi \) dm\(^3\).
B. \(30\pi \) dm\(^3\).
C. \(50\pi \) dm\(^3\).
D. \(60\pi \) dm\(^3\).
Phương pháp:
Thể tích khối trụ bằng diện tích đáy nhân chiều cao.
Lời giải:
Thể tích của khối trụ đó là: \(V = \pi {.5^2}.6 = 150\pi \left( {d{m^3}} \right)\).
Đáp án: A
II. PHẦN TỰ LUẬN (8,0 điểm)
Câu 1: (1 điểm) Trong một hộp kín đựng 10 tấm thẻ được đánh số tự nhiên từ 1 đến 10, không có hai thẻ nào được đánh số giống nhau. Lấy ngẫu nhiên một tấm thẻ từ trong hộp đã cho. Tính xác suất của biến cố A: "Lấy được thẻ ghi số chẵn".
Lời giải:
Không gian mẫu của phép thử là: \(\Omega = \left\{ {1;2;3;4;5;6;7;8;9;10} \right\}\) gồm 10 phần tử
Có 5 kết quả thuận lợi cho biến cố A là 2; 4; 6; 8; 10
Vậy xác suất của biến cố A là \(\frac{5}{{10}} = \frac{1}{2}\)
Câu 2: (1 điểm) Cho biểu thức \(P = \left( {\frac{1}{{\sqrt x + 1}} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x }}{{\sqrt x - 1}}\) (với điều kiện \(x > 0\), \(x \ne 1\)).
a) Rút gọn biểu thức \(P\).
b) Tìm tất cả các giá trị thực của \(x\) để \(23x.P = 2025\).
Lời giải:
a) \(P = \left( {\frac{1}{{\sqrt x + 1}} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x }}{{\sqrt x - 1}}\) (với điều kiện \(x > 0\), \(x \ne 1\))
\( = \left[ {\frac{{\sqrt x - 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{{\sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}} \right]:\frac{{\sqrt x }}{{\sqrt x - 1}}\)
\( = \frac{{\sqrt x - 1 + \sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}:\frac{{\sqrt x }}{{\sqrt x - 1}}\)
\( = \frac{{2\sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}.\frac{{\sqrt x - 1}}{{\sqrt x }}\)
\( = \frac{2}{{\sqrt x + 1}}\).
Vậy \(P = \frac{2}{{\sqrt x + 1}}\) với điều kiện \(x > 0\), \(x \ne 1\).
b) \(23x.P = 2025\) (với điều kiện \(x > 0\), \(x \ne 1\))
\(23x.\frac{2}{{\sqrt x + 1}} = 2025\)
\(46x = 2025\left( {\sqrt x + 1} \right)\)
\(46x - 2025\sqrt x - 2025 = 0\) (*)
Đặt \(t = \sqrt x \) \((t > 0)\). Khi đó phương trình (*) trở thành:
\(46{t^2} - 2025t - 2025 = 0\) (**)
Ta có \(\Delta = {b^2} - 4ac = {( - 2025)^2} - 4.46.( - 2025) = 4473225 > 0\).
Do đó, phương trình (**) có hai nghiệm phân biệt:
\({t_1} = \frac{{ - b + \sqrt \Delta }}{{2a}} = \frac{{ - ( - 2025) + \sqrt {4473225} }}{{2.46}} = 45\) (TM);
\({t_2} = \frac{{ - b - \sqrt \Delta }}{{2a}} = \frac{{ - ( - 2025) - \sqrt {4473225} }}{{2.46}} = - \frac{{45}}{{46}}\) (loại).
Với \({t_1} = 45\) thì \(\sqrt x = 45\), suy ra \(x = 2025\) (thỏa mãn).
Vậy để \(23x.P = 2025\) thì \(x = 2025\).
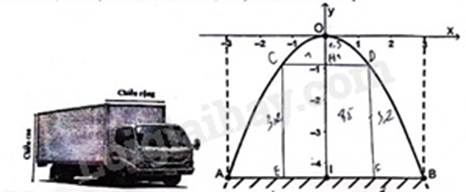
Câu 3: (1 điểm) Một cái cổng được thiết kế dạng parabol có phương trình biểu diễn trong hệ trục toạ độ Oxy là \(y = a{x^2}\) (với a là hằng số khác 0). Biết khoảng cách giữa hai chân cổng là AB = 6m, chiều cao từ điểm chính giữa cổng đến mặt đấy là OI = 4,5m (tham khảo hình vẽ sau).
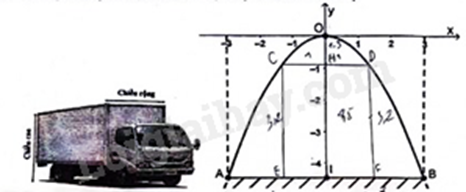
a) Tìm hệ số a dựa vào dữ kiện đã cho.
b) Một xe tải có chiều rộng bằng 2m, chiều cao bằng 3,2m (tham khảo hình vẽ trên) đi vào chính giữa cổng trên. Hỏi xe tải này có thể đi qua được cổng đó mà không chạm vào cổng hay không? Giải thích lý do.
Lời giải:
a) Vì parabol đi qua điểm A(-3; - 4,5) nên ta có:
\(\begin{array}{l} - 4,5 = a.{\left( { - 3} \right)^2}\\a = \frac{{ - 4,5}}{{{{\left( { - 3} \right)}^2}}} = \frac{{ - 1}}{2}\end{array}\)
Vậy hệ số \(a = \frac{{ - 1}}{2}\).
b)
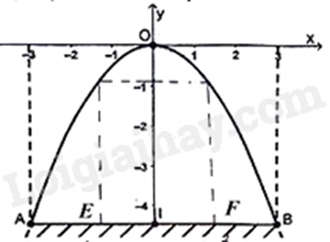
Chiếc xe tải có chiều rộng bằng 2m nên khoảng cách EI = IF = \(\frac{2}{2} = 1\left( m \right)\).
Với \(x = 1\) thì \(y = \frac{{ - 1}}{2}{.1^2} = \frac{{ - 1}}{2}\) nên chiều cao tối đa của chiếc xe có thể đi qua cổng là:
\(4,5 - \left| {\frac{{ - 1}}{2}} \right| = 4,5 - \frac{1}{2} = 4 > 3,2\)
Vậy xe tải này có thể đi qua được cổng đó mà không chạm vào cổng.
Câu 4: (1 điểm) Bác Vĩnh và bác Phúc cùng gửi tiền tiết kiệm vào ngân hàng với tổng số tiền là 900 triệu đồng. Bác Vĩnh gửi vào ngân hàng A với lãi suất 7% một năm, bác Phúc gửi vào ngân hàng B với lãi suất 6% một năm. Sau khi gửi được đúng một năm, tổng số tiền lãi mà hai bác nhận được là 60 triệu đồng. Hỏi ban đầu mỗi bác gửi tiết kiệm bao nhiêu tiền?
Lời giải:
Gọi số tiền bác Vĩnh gửi là \(x\) (triệu đồng), \(0 < x < 900\)
Số tiền bác Phúc gửi là \(900 - x\) (triệu đồng)
Bác Vĩnh gửi với lãi suất 7% một năm, tức là số tiền lãi: \(0,07x\) (triệu đồng)
Bác Phúc gửi với lãi suất 6% một năm, tức là số tiền lãi: \(0,06.\left( {900 - x} \right)\) (triệu đồng)
Tổng số tiền lãi cả hai bác nhận được là: \(0,07x + 0,06.\left( {900 - x} \right)\) (triệu đồng)
Vì tổng số tiền lãi cả hai bác nhận được là 60 triệu đồng nên ta có phương trình:
\(\begin{array}{l}0,07x + 0,06.\left( {900 - x} \right) = 60\\0,07x + 54 - 0,06x - 60 = 0\\0,01x - 6 = 0\\x = 600{\rm{ (TM)}}\end{array}\)
Vậy số tiền ban đầu bác Vĩnh gửi là 600 triệu đồng, số tiền bác Phúc gửi là 300 triệu đồng.
Câu 5: (3 điểm) Cho nửa đường tròn đường kính AB, có tâm là điểm O. Đường thẳng đi qua tâm O và vuông góc với đường kính AB cắt nửa đường tròn đã cho tại điểm C. Trên tia đối của tia CA lấy điểm D (D không trùng với C), kẻ CH vuông góc với đường thẳng BD tại điểm H.
a) Chứng minh tứ giác OBHC nội tiếp.
b) Gọi E là giao điểm của hai đường thẳng HO và BC. Chứng minh HO là tia phân giác của \(\angle CHB\) và \(CE \cdot CH = BE \cdot HD\).
c) Đường tròn ngoại tiếp tam giác CDH cắt nửa đường tròn đường kính AB tại điểm K (K không trùng với C). Chứng minh \(DE > 2.CK\).
Lời giải:
a)
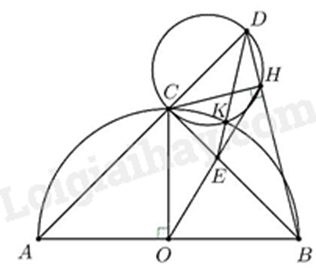
Do \(OC \bot AB\) tại O nên \(\Delta COB\) vuông tại O nên C, O, B cùng thuộc đường tròn đường kính CB
Có \(CH \bot BD\) tại H nên \(\Delta CBH\) vuông tại H nên C, H, B cùng thuộc đường tròn đường kính CB
Vậy C, H, B, O cùng thuộc đường tròn đường kính CB hay tứ giác OBHC nội tiếp.
b) Ta có \(OC = OB\) (cùng bằng bán kính của \(\left( O \right)\)) nên \(\Delta OBC\) vuông cân tại O
Khi đó \(\angle OCB = \angle OBC = 45^\circ \)
Do OBHC nội tiếp nên \(\angle CHO = \angle CBO = 45^\circ \) (cùng chắn cung CO)
và \(\angle OHB = \angle OCB = 45^\circ \) (cùng chắn cung OB)
Suy ra \(\angle CHO = \angle OHB = 45^\circ \) hay OH là phân giác của \(\angle CHB\).
Do OH là phân giác của \(\angle CHB\) nên \(\frac{{CE}}{{BE}} = \frac{{CH}}{{HB}}\) (tính chất đường phân giác)
Do \(C \in \left( O \right)\) nên \(\angle ACB = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) suy ra \(CB \bot CD\) tại C
Suy ra \(\angle DCH + \angle HCB = 90^\circ \)
Mà \(\angle CBH + \angle BCH = 180^\circ - \angle CHB = 90^\circ \) nên \(\angle DCH = \angle CBH\) (cùng cộng \(\angle BCH\) bằng \(90^\circ \))
Kết hợp \(\angle CHB = \angle CHD = 90^\circ \) suy ra $\Delta DHC\backsim \Delta CHB\left( g.g \right)$
Suy ra \(\frac{{DH}}{{CH}} = \frac{{HC}}{{HB}}\).
Mà \(\frac{{CE}}{{BE}} = \frac{{CH}}{{HB}}\) nên \(\frac{{DH}}{{CH}} = \frac{{CE}}{{BE}}\) hay \(DH.BE = CE.CH\)
c)
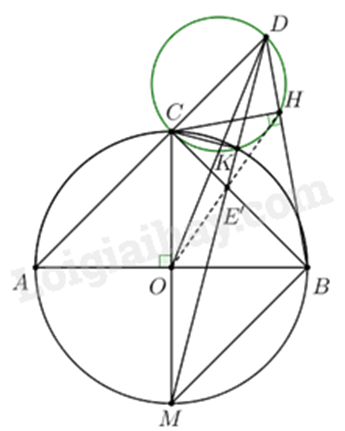
Kẻ đường kính CM của \(\left( O \right)\). Do \(K \in \left( O \right)\) nên \(KM \bot CK\)
Lại có \(K\) thuộc đường tròn đường kính CD nên \(\angle CKD = 90^\circ \) hay \(DK \bot CK\)
Suy ra \(D,K,M\) thẳng hàng
Gọi E’ là giao điểm của CB và DM.
Do CM là đường kính nên \(\angle CBM = 90^\circ \) nên \(BM \bot CB\)
Mà \(CD \bot BC\) nên \(BM\parallel CD\)
Khi đó \(\frac{{CE'}}{{E'B}} = \frac{{CD}}{{BM}}\) (Thalès). Mà \(BM = BC\) nên \(\frac{{CD}}{{BM}} = \frac{{CD}}{{BC}} = \tan \angle CBD = \frac{{CH}}{{BH}}\)
Vậy \(\frac{{CE'}}{{E'B}} = \frac{{CH}}{{HB}}\) suy ra \(HE'\) là phân giác của \(\angle CHB\)
Mà HE là phân giác của \(\angle CHB\) nên \(E \equiv E'\) hay D, E, K, M thẳng hàng.
Ta có \(\angle CDE = \angle ECK\) (do cùng cộng với \(\angle DCK\) bằng \(90^\circ \))
Kết hợp \(\angle CKD = \angle CKE = 90^\circ \). Khi đó
Suy ra \(\frac{{CK}}{{EK}} = \frac{{DK}}{{CK}}\) hay \(C{K^2} = EK.DK\)
Lại có \(EK.DK \le \frac{{{{\left( {EK + DK} \right)}^2}}}{4} = \frac{{D{E^2}}}{4}\) nên \(C{K^2} \le \frac{{D{E^2}}}{4}\)
Suy ra \(CK \le \frac{{DE}}{2}\) hay \(DE \ge 2CK\)
Dấu “=” xảy ra khi K là trung điểm của DE hay K phải thoả mãn \(\angle KCD = 45^\circ \), mà \(\angle ACM = 45^\circ \) nên \(\angle MCK = 90^\circ \) (vô lý)
Vậy \(DE > 2CK\) (đpcm)
Câu 6: (1 điểm) Cho \(a,{\mkern 1mu} b,{\mkern 1mu} c\) là các số thực dương thỏa mãn \(ab + 4bc + 4ca = 28\). Tìm giá trị nhỏ nhất của biểu thức \(T = \frac{{11a + 11b + 24c}}{{\sqrt {8{a^2} + 224} + \sqrt {8{b^2} + 224} + \sqrt {16{c^2} + 28} }}\).
Lời giải:
Vì \(ab + 4bc + 4ca = 28\) nên ta có:
\(\sqrt {8{a^2} + 224} = \sqrt {8{a^2} + 8\left( {ab + 4bc + 4ca} \right)} \)
\( = \sqrt {8\left( {{a^2} + ab + 4bc + 4ca} \right)} = \sqrt {8\left( {a + 4c} \right)\left( {a + b} \right)} \)
\(\sqrt {8{b^2} + 224} = \sqrt {8{b^2} + 8\left( {ab + 4bc + 4ca} \right)} \)
\( = \sqrt {8\left( {{b^2} + ab + 4bc + 4ca} \right)} = \sqrt {8\left( {b + 4c} \right)\left( {a + b} \right)} \)
\(\sqrt {16{c^2} + 28} = \sqrt {16{c^2} + ab + 4bc + 4ca} = \sqrt {\left( {a + 4c} \right)\left( {b + 4c} \right)} \)
Áp dụng bất đẳng thức Cauchy cho hai số không âm ta có:
\(\sqrt {8{a^2} + 224} = \sqrt {\left( {2a + 8c} \right)\left( {4a + 4b} \right)} \)
\( = \sqrt {\left( {2a + 8c} \right)\left( {4a + 4b} \right)} \le \frac{{2a + 8c + 4a + 4b}}{2} = \frac{{6a + 4b + 8c}}{2}\)
\(\sqrt {8{b^2} + 224} = \sqrt {\left( {2b + 8c} \right)\left( {4a + 4b} \right)} \)
\( = \sqrt {\left( {2b + 8c} \right)\left( {4a + 4b} \right)} \le \frac{{2b + 8c + 4b + 4a}}{2} = \frac{{4a + 6b + 8c}}{2}\)
\(\sqrt {16{c^2} + 28} = \sqrt {\left( {a + 4c} \right)\left( {b + 4c} \right)} \le \frac{{a + b + 8c}}{2}\)
Suy ra:
\(\sqrt {8{a^2} + 224} + \sqrt {8{b^2} + 224} + \sqrt {16{c^2} + 28} \)
\( \le \frac{{6a + 4b + 8c}}{2} + \frac{{4a + 6b + 8c}}{2} + \frac{{a + b + 8c}}{2} = \frac{{11a + 11b + 24c}}{2}\)
Do đó: \(T \ge 2\)
Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}2a + 8c = 4a + 4b\\2b + 8c = 4a + 4b\\a + 4c = b + 4c\\ab + 4bc + 4ca = 28\end{array} \right.\) suy ra \(a = b = 2;c = \frac{3}{2}\)
Vậy giá trị nhỏ nhất của T là 2 khi \(a = b = 2;c = \frac{3}{2}\)
II. PHẦN TỰ LUẬN (8,0 điểm)













Danh sách bình luận