Đề thi vào 10 môn Toán Trà Vinh năm 2018
Tải vềBài 1 (VD). (3,0 điểm) Rút gọn biểu thức
Đề bài
Bài 1 (VD). (3,0 điểm)
- Rút gọn biểu thức \(2\sqrt {75} + 3\sqrt {48} - 4\sqrt {27} \)
- Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right.\)
- Giải phương trình \(3{x^2} - 7x + 2 = 0\)
Bài 2 (VD) (2 điểm)
Cho hai hàm số: \(y = - x + 2\) và \(y = {x^2}\) có đồ thị lần lượt là \(\left( d \right)\) và \(\left( P \right).\)
1) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng hệ trục tọa độ.
2) Bằng phép toán tìm tọa độ giao điểm của \(\left( d \right)\) và \(\left( P \right).\)
Bài 3 (VD) (1 điểm)
Cho phương trình \({x^2} - \left( {m + 1} \right)x + m - 2 = 0\) (với m là tham số).
1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.
2) Tìm các số nguyên m để phương trình có nghiệm nguyên.
Bài 4 (VD). (1,0 điểm)
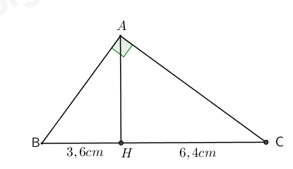
Cho tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết BH = 3,6cm và HC = 6,4 cm. Tính độ dài BC, AH, AB, AC.
Bài 5 (VD). (3 điểm).
Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), M là trung điểm của cạnh AC. Đường tròn đường kính MC cắt BC tại N. Đường thẳng BM cắt đường tròn đường kính MC tại D.
1. Chứng minh tứ giác BADC nội tiếp.
2. Chứng minh DB là phân giác của góc ADN.
3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.
Lời giải
Bài 1.
Phương pháp:
- Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|B = \left\{ \begin{array}{l}AB,\,\,A \ge 0\\ - AB,\,\,A < 0\end{array} \right.\)
- Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.
- Sử dụng biệt thức \(\Delta = {b^2} - 4ac\) để giải phương trình bậc hai.
Cách giải:
1. Rút gọn biểu thức \(2\sqrt {75} + 3\sqrt {48} - 4\sqrt {27} \)
Ta có:
\(\begin{array}{l}\;\;\;2\sqrt {75} + 3\sqrt {48} - 4\sqrt {27} \\ = 2\sqrt {{5^2}.3} + 3\sqrt {{4^2}.3} - 4\sqrt {{3^2}.3} \\ = 10\sqrt 3 + 12\sqrt 3 - 12\sqrt 3 \\ = 10\sqrt 3 .\end{array}\)
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right.\)
\(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\3x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\3x + 2\left( {2x - 8} \right) = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\7x = 21\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2x - 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {3; - 2} \right)\)
3. Giải phương trình \(3{x^2} - 7x + 2 = 0\)
Ta có: \(a = 3;\;\;b = - 7;\;\;c = 2\)
\(\Delta = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4.3.2 = 25 > 0 \Rightarrow \sqrt \Delta = 5\)
Khi đó phương trình đã cho có hai nghiệm phân biệt là: \(\left[ \begin{array}{l}{x_1} = \dfrac{{7 - 5}}{6} = \dfrac{1}{3}\\{x_2} = \dfrac{{7 + 5}}{6} = 2\end{array} \right.\)
Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ {\dfrac{1}{3};2} \right\}\)
Bài 2: Cho hai hàm số: \(y = - x + 2\) và \(y = {x^2}\) có đồ thị lần lượt là \(\left( d \right)\) và \(\left( P \right).\)
Phương pháp:
1) Lập bảng giá trị các điểm mà từng đồ thị đi qua sau đó vẽ cả 2 đồ thị đã cho trên cùng hệ trục tọa độ.
2) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
+) Giải phương trình hoành độ tìm hoành độ giao điểm sau đó thể vào một trong hai phương trình của hai đồ thị để tìm tung độ.
Cách giải:
1) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng hệ trục tọa độ.
+) Vẽ đồ thị hàm số: \(\left( d \right):\;\;y = - x + 2.\)
|
\(x\) |
\(0\) |
\(2\) |
|
\(y = - x + 2\) |
\(2\) |
\(0\) |
+) Vẽ đồ thị hàm số: \(\left( P \right):\;\;y = {x^2}.\)
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y = {x^2}\) |
\(4\) |
\(1\) |
\(0\) |
\(1\) |
\(4\) |
Đồ thị hàm số:
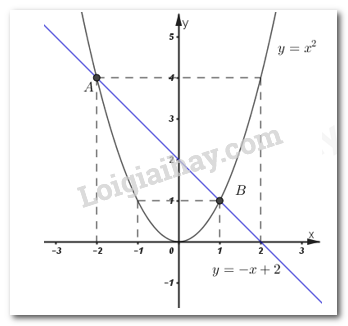
2) Bằng phép toán tìm tọa độ giao điểm của \(\left( d \right)\) và \(\left( P \right).\)
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
Ta có phương trình hoành độ giao điểm của hai đồ thị là:
\(\begin{array}{l} - x + 2 = {x^2}\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = 4\\x = 1 \Rightarrow y = 1\end{array} \right..\end{array}\)
Vậy hai đồ thị cắt nhau tại hai điểm phân biệt \(A\left( { - 2;\;4} \right)\) và \(B\left( {1;\;1} \right).\)
Bài 3:
Phương pháp:
+) Phương trình có hai nghiệm phân biệt với mọi \(m \Leftrightarrow \Delta > 0\;\;\forall m.\)
+) Từ phương trình đã cho, cô lập m, đưa phương trình về dạng \(m = A\left( x \right) + \dfrac{C}{{B\left( x \right)}}\) , với C là hằng số, tìm điều kiện để C chia hết cho B(x), tức là B(x) là ước của C.
Cách giải:
1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.
Ta có: \(\Delta = {\left( {m + 1} \right)^2} - 4\left( {m - 2} \right) = {m^2} + 2m + 1 - 4m + 8 = {m^2} - 2m + 1 + 8 = {\left( {m - 1} \right)^2} + 8.\)
Vì \({\left( {m - 1} \right)^2} \ge 0\;\;\forall m \Rightarrow {\left( {m - 1} \right)^2} + 8 > 0\;\forall m.\)
Hay \(\Delta > 0\;\forall m \Rightarrow \) phương trình luôn có hai nghiệm phân biệt với mọi \(m.\)
2) Tìm các số nguyên m để phương trình có nghiệm nguyên.
Phương trình đã cho luôn có hai nghiệm phân biệt với mọi \(m.\)
Đề bài yêu cầu tìm \(m \in Z\) để \(x \in Z.\) Ta đưa bài toán về dạng tìm x nguyên để m nguyên.
Ta có: \({x^2} - \left( {m + 1} \right)x + m - 2 = 0 \Leftrightarrow {x^2} - mx - x + m - 2 = 0\)
\(\begin{array}{l} \Leftrightarrow {x^2} - x - 2 = m\left( {x - 1} \right)\\ \Leftrightarrow m = \dfrac{{{x^2} - x - 2}}{{x - 1}} = \dfrac{{x\left( {x - 1} \right) - 2}}{{x - 1}}\;\;\left( {x \ne 1} \right)\\ \Leftrightarrow m = x - \dfrac{2}{{x - 1}}.\\ \Rightarrow m \in Z \Leftrightarrow \left( {x - \dfrac{2}{{x - 1}}} \right) \in Z \Leftrightarrow \dfrac{2}{{x - 1}} \in Z\,\,\left( {Do\,\,x \in Z} \right) \Leftrightarrow \left( {x - 1} \right) \in U\left( 2 \right).\end{array}\)
Mà \(U\left( 2 \right) = \left\{ { - 2;\; - 1;\;1;\;2} \right\}.\)
\( \Rightarrow \left[ \begin{array}{l}x - 1 = - 2\\x - 1 = - 1\\x - 1 = 1\\x - 1 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 2\\x = 3\end{array} \right.\,\,\left( {tm} \right) \Rightarrow \left[ \begin{array}{l}m = 0\\m = 2\\m = 0\\m = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\;\;\left( {tm} \right)\\m = 2\;\;\;\left( {tm} \right)\end{array} \right..\)
Vậy với \(m = 0\) và \(m = 2\) thỏa mãn yêu cầu bài toán.
Bài 4.
Phương pháp:
Áp dụng hệ thức lượng trong tam giác vuông ABC với chiều cao AH để tính AH: \(A{H^2} = BH.CH\)
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H để tính AB: \(A{H^2} + B{H^2} = A{B^2}\)
Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A để tính AC: \(A{C^2} = B{C^2} - A{B^2}.\)
Cách giải:
Ta có: \(\left( {H \in BC} \right)\) nên : \(BC = BH + HC = 3,6 + 6,4 = 10\left( {cm} \right)\)
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A với đường cao AH ta có:
\(A{H^2} = BH.HC \Rightarrow A{H^2} = 3,6.6,4 = 23,04 \Rightarrow AH = 4,8\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
\(A{B^2} = A{H^2} + B{H^2} = 4,{8^2} + 3,{6^2} = 36 \Rightarrow AB = 6\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
\(A{C^2} = B{C^2} - A{B^2} = {10^2} - {6^2} = 64 \Rightarrow AC = 8\left( {cm} \right)\)
Vậy: BC = 10 cm; AH = 4,8 cm; AB = 6 cm; AC = 8 cm.
Bài 5.
Phương pháp:
1. Chứng minh tứ giác BADC có hai đỉnh A và D cùng nhìn BC dưới các góc bằng nhau.
2. Chứng minh hai góc ADB và BDN cùng bằng góc ACB.
3. Chứng minh M là trực tâm của tam giác PBC \( \Rightarrow PM \bot BC\)
Chứng minh \(MN \bot BC\), từ đó suy ra P, M, N thẳng hàng.
Cách giải:
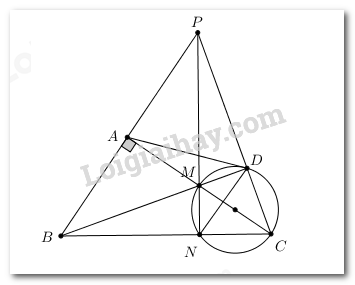
1. Chứng minh tứ giác BADC nội tiếp.
Ta có \(\widehat {MDC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính MC) \( \Rightarrow \widehat {BDC} = {90^0}\).(Do B, M, D thẳng hàng)
Có \(\widehat {BAC} = {90^0}\) (do giả thiết tam giác ABC vuông tại A)
Xét tứ giác BADC có \(\widehat {BAC} = \widehat {BDC} = {90^0} \Rightarrow \) Hai điểm A và D cùng nhìn BC dưới góc 900 \( \Rightarrow \) Tứ giác BADC là tứ giác nội tiếp (Tứ giác có hai đỉnh cùng nhìn 1 cạnh dưới các góc bằng nhau).
2. Chứng minh DB là phân giác của góc ADN.
Do BADC là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {ADB} = \widehat {ACB}\) (hai góc nội tiếp cùng chắn cung AB).
Lại có \(\widehat {ACB} = \widehat {MCN} = \widehat {MDN}\) (hai góc nội tiếp cùng chắn cung MN của đường tròn đường kính MC).
\( \Rightarrow \widehat {ADB} = \widehat {MDN} = \widehat {BDN} \Rightarrow BD\) là tia phân giác của góc ADN.
3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.
Ta có \(\widehat {BDC} = {90^0}\,\,\left( {cmt} \right) \Rightarrow BD \bot DC \Rightarrow BD \bot PC\)
Tam giác ABC vuông tại A \( \Rightarrow AC \bot AB \Rightarrow AC \bot PB\)
Xét tam giác PBC có \(BD \bot PC;\,\,AC \bot PB;\,\,AC \cap BD = M \Rightarrow M\) là trực tâm tam giác PBC.
\( \Rightarrow PM \bot BC\).
Lại có \(\widehat {MNC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính MC) \( \Rightarrow MN \bot NC \Rightarrow MN \bot BC\)
Qua điểm M nằm ngoài đường thẳng BC ta kẻ được \(PM \bot BC\) và \(MN \bot BC\)
\( \Rightarrow PM \equiv MN\) hay ba điểm P, M, N thẳng hàng.













Danh sách bình luận