Đề thi vào 10 môn Toán trường THPT Chuyên Khoa học Tự nhiên (Vòng 1) năm 2025

Đề bài

Câu 1: (3,5 điểm) a) Giải phương trình \(x + 2\sqrt {\left( {x + 1} \right)\left( {x + 6} \right)}  + 2\sqrt {x + 1}  = 2 + 2\sqrt {x + 6} \)

b) Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} + 6{y^2} + 7xy + x + 6y = 21\\21\left( {22 - 5{y^2} - 5xy + x - 4y} \right) = 27\left( {x + 6y} \right)\end{array} \right.\)

Câu 2: (2,5 điểm) a) Tìm tất cả các cặp số nguyên \(x,\,\,y\) thỏa mãn \(y + \frac{1}{y} = \frac{{{x^4} + 6{x^2} + 1}}{{2x\left( {{x^2} + 1} \right)}}\)

b) Xét các số thực dương \(a,\,\,b,\,\,c\) thỏa mãn \(a + b + c = \frac{3}{2}\)

Tìm giá trị nhỏ nhất của biểu thức

\(M = \frac{{\sqrt[3]{a}}}{{{{\left( {2 - a} \right)}^2}\left( {a + 2b} \right)}} + \frac{{\sqrt[3]{b}}}{{{{\left( {2 - b} \right)}^2}\left( {b + 2c} \right)}} + \frac{{\sqrt[3]{c}}}{{{{\left( {2 - c} \right)}^2}\left( {c + 2a} \right)}}\)

Câu 3: (3 điểm) Cho tam giác \(ABC\) nhọn, không cân. Trên các cạnh \(CA\) và \(AB\) lần lượt lấy các điểm \(E,\,\,F\) (không trùng với các đỉnh của tam giác) sao cho \(AE = AF\). Trên đường thẳng \(EF\), lấy các điểm \(M,\,\,N\) sao cho đường thẳng \(CM\) vuông góc với đường thẳng \(CA\) và đường thẳng \(BN\) vuông góc với đường thẳng \(BA\). Gọi \(K\) là giao điểm của hai đường thẳng \(BN\) và \(CM\).

a) Chứng minh rằng \(KN = KM\)

b) Dựng các hình bình hành \(ANQF\) và \(AMRE\). Chứng minh rằng \(\angle NQK = \angle MRK\)

c) Gọi \(L,\,\,J\) lần lượt là hình chiếu vuông góc của các điểm \(M,\,\,N\) trên đường thẳng \(BC\); \(S\) là giao điểm của hai đường thẳng \(JF\) và \(LE;\,\,T\) là điểm đối xứng với điểm \(S\) qua đường thẳng \(EF\). Chứng minh rằng ba điểm \(A,\,\,T,\,\,K\) thẳng hàng

Câu 4: (1 điểm) Tìm số nguyên dương \(k\) nhỏ nhất sao cho với mọi cách sắp xếp 99 điểm màu đỏ và 100 điểm màu xanh trên mặt phẳng (không có ba điểm nào thẳng hàng), ta luôn vẽ được \(k\) đường thẳng, mỗi đường thẳng không đi qua điểm nào trong các điểm trên và các đường thẳng đó chia mặt phẳng thành các miền mà trong mỗi miền không có hai điểm khác màu

-------- Hết --------

Lời giải

Câu 1: (3,5 điểm) a) Giải phương trình \(x + 2\sqrt {\left( {x + 1} \right)\left( {x + 6} \right)}  + 2\sqrt {x + 1}  = 2 + 2\sqrt {x + 6} \)

b) Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} + 6{y^2} + 7xy + x + 6y = 21\\21\left( {22 - 5{y^2} - 5xy + x - 4y} \right) = 27\left( {x + 6y} \right)\end{array} \right.\)

Lời giải:

a) Điều kiện xác định \(x \ge  - 1\)

Trường hợp 1: \(x > 0\)

Vì \(x > 0\) nên \(x + 1 > 1\)

Do đó \(2\sqrt {\left( {x + 1} \right)\left( {x + 6} \right)}  > 2\sqrt {x + 6} \) và \(x + 2\sqrt {x + 1}  > 0 + 2 = 2\)

Khi đó \(x + 2\sqrt {\left( {x + 1} \right)\left( {x + 6} \right)}  + 2\sqrt {x + 1}  > 2 + 2\sqrt {x + 6} \)

Trường hợp 2: \( - 1 \le x < 0\)

Vì \( - 1 \le x < 0\) nên \(0 \le x + 1 < 1\)

Do đó \(2\sqrt {\left( {x + 1} \right)\left( {x + 6} \right)}  < 2\sqrt {x + 6} \) và \(x + 2\sqrt {x + 1}  < 0 + 2 = 2\)

Khi đó \(x + 2\sqrt {\left( {x + 1} \right)\left( {x + 6} \right)}  + 2\sqrt {x + 1}  < 2 + 2\sqrt {x + 6} \)

Trường hợp 3: \(x = 0\)

Thay \(x = 0\) vào phương trình đã cho ta thấy thỏa mãn

Vậy phương trình có nghiệm duy nhất \(x = 0\)

b) Phương trình thứ nhất viết lại thành \(\left( {x + 6y} \right)\left( {x + y + 1} \right) = 21\,\,\left( 1 \right)\)

Từ đây suy ra \(x + 6y \ne 0\)

Thay vào phương trình thứ hai \(21\left( {21 + 1 - 5{y^2} - 5xy + x - 4y} \right) = 27\left( {x + 6y} \right)\) ta có

\(\left( {x + 6y} \right)\left( {x + y + 1} \right)\left[ {\left( {x + 6y} \right)\left( {x + y + 1} \right) + 1 - 5{y^2} - 5xy + x - 4y} \right] = 27\left( {x + 6y} \right)\)

Hay \(\left( {x + 6y} \right)\left( {x + y + 1} \right){\left( {x + y + 1} \right)^2} = 27\left( {x + 6y} \right)\)

Suy ra \(\left( {x + 6y} \right){\left( {x + y + 1} \right)^3} = 27\left( {x + 6y} \right)\)

Do \(x + 6y \ne 0\) nên \({\left( {x + y + 1} \right)^3} = 27\) hay \(x + y = 2\,\,\left( 2 \right)\)

Kết hợp với (1) ta được \(x + 6y = 7\,\,\left( 3 \right)\)

Từ (2) và (3) ta được \(x = 1,\,\,y = 1\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {1;1} \right)\)

Câu 2: (2,5 điểm) a) Tìm tất cả các cặp số nguyên \(x,\,\,y\) thỏa mãn \(y + \frac{1}{y} = \frac{{{x^4} + 6{x^2} + 1}}{{2x\left( {{x^2} + 1} \right)}}\)

b) \(M = \frac{{\sqrt[3]{a}}}{{{{\left( {2 - a} \right)}^2}\left( {a + 2b} \right)}} + \frac{{\sqrt[3]{b}}}{{{{\left( {2 - b} \right)}^2}\left( {b + 2c} \right)}} + \frac{{\sqrt[3]{c}}}{{{{\left( {2 - c} \right)}^2}\left( {c + 2a} \right)}}\)

Lời giải:

a) Điều kiện \(x \ne 0,\,\,y \ne 0\)

Ta có: \(y + \frac{1}{y} = \frac{{{x^2} + 1}}{{2x}} + \frac{{2x}}{{{x^2} + 1}}\)

Hay \(\left( {y - \frac{{{x^2} + 1}}{{2x}}} \right) + \left( {\frac{1}{y} - \frac{{2x}}{{{x^2} + 1}}} \right) = 0\)

Do đó \(\left( {y - \frac{{{x^2} + 1}}{{2x}}} \right)\left[ {1 - \frac{{2x}}{{y\left( {{x^2} + 1} \right)}}} \right] = 0\)

Trường hợp 1: \(y = \frac{{{x^2} + 1}}{{2x}}\)

Vì \(y \in \mathbb{Z}\) nên \(\left( {{x^2} + 1} \right) \vdots x\)

Suy ra \(1 \vdots x\) (vì \({x^2} \vdots x\))

Mà \(x \in \mathbb{Z}\) nên \(x =  \pm 1\)

Trường hợp 2: \(1 - \frac{{2x}}{{y\left( {{x^2} + 1} \right)}} = 0\)

Khi đó \(y = \frac{{2x}}{{{x^2} + 1}}\)

Vì \(0 < \frac{{2x}}{{{x^2} + 1}} \le 1\) nên \(0 < y \le 1\)

Mà \(y \in \mathbb{Z}\) nên \(y = 1\)

Do đó \(\frac{{2x}}{{{x^2} + 1}} = 1\) hay \({\left( {x - 1} \right)^2} = 0\)

Khi đó \(x = 1\)

Thử lại ta thấy các giá trị \(x,\,\,y\) tìm được đều thỏa mãn

Vậy các cặp số \(\left( {x;y} \right)\) thỏa mãn là \(\left( {1;1} \right)\) và \(\left( { - 1; - 1} \right)\)

b) Ta có: \(M = \frac{a}{{\sqrt[3]{{{a^2}}}{{\left( {2 - a} \right)}^2}\left( {a + 2b} \right)}} + \frac{b}{{\sqrt[3]{{{b^2}}}{{\left( {2 - b} \right)}^2}\left( {b + 2c} \right)}} + \frac{c}{{\sqrt[3]{{{c^2}}}{{\left( {2 - c} \right)}^2}\left( {c + 2a} \right)}}\)

Áp dụng bất đẳng thức Cauchy ta có

\(\sqrt[3]{{{a^2}}} = \sqrt[3]{2}.\sqrt[3]{{a.a.\frac{1}{2}}} \le \sqrt[3]{2}.\frac{{a + a + \frac{1}{2}}}{3} = \frac{{\sqrt[3]{2}}}{6}\left( {4a + 1} \right)\)

Do đó

\(\begin{array}{l}\sqrt[3]{{{a^2}}}{\left( {2 - a} \right)^2} \le \frac{{\sqrt[3]{2}}}{6}\left( {4a + 1} \right){\left( {2 - a} \right)^2} = \frac{{\sqrt[3]{2}}}{{24}}\left( {4a + 1} \right)\left( {4 - 2a} \right)\left( {4 - 2a} \right)\\ \le \frac{{\sqrt[3]{2}}}{{24}}.\frac{{{{\left( {4a + 1 + 4 - 2a + 4 - 2a} \right)}^3}}}{{27}} = \frac{9}{8}\sqrt[3]{2}\end{array}\)

Do đó \(M \ge \frac{8}{{9\sqrt[3]{2}}}\left( {\frac{a}{{a + 2b}} + \frac{b}{{b + 2c}} + \frac{c}{{c + 2a}}} \right)\)

Ta có:

\(\frac{a}{{a + 2b}} + \frac{b}{{b + 2c}} + \frac{c}{{c + 2a}} = \frac{{{a^2}}}{{{a^2} + 2ab}} + \frac{{{b^2}}}{{{b^2} + 2bc}} + \frac{{{c^2}}}{{{c^2} + 2ca}}\)

\( \ge \frac{{{{\left( {a + b + c} \right)}^2}}}{{{a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca}} = 1\)

Như vậy \(M \ge \frac{8}{{9\sqrt[3]{2}}} = \frac{{4\sqrt[3]{4}}}{9}\)

Dấu  xảy ra khi và chỉ khi \(a = b = c = \frac{1}{2}\)

Vậy giá trị nhỏ nhất của \(M = \frac{{4\sqrt[3]{4}}}{9}\) xảy ra khi \(a = b = c = \frac{1}{2}\)

Câu 3: (3 điểm) Cho tam giác \(ABC\) nhọn, không cân. Trên các cạnh \(CA\) và \(AB\) lần lượt lấy các điểm \(E,\,\,F\) (không trùng với các đỉnh của tam giác) sao cho \(AE = AF\). Trên đường thẳng \(EF\), lấy các điểm \(M,\,\,N\) sao cho đường thẳng \(CM\) vuông góc với đường thẳng \(CA\) và đường thẳng \(BN\) vuông góc với đường thẳng \(BA\). Gọi \(K\) là giao điểm của hai đường thẳng \(BN\) và \(CM\).

a) Chứng minh rằng \(KN = KM\)

b) Dựng các hình bình hành \(ANQF\) và \(AMRE\). Chứng minh rằng \(\angle NQK = \angle MRK\)

c) Gọi \(L,\,\,J\) lần lượt là hình chiếu vuông góc của các điểm \(M,\,\,N\) trên đường thẳng \(BC\); \(S\) là giao điểm của hai đường thẳng \(JF\) và \(LE;\,\,T\) là điểm đối xứng với điểm \(S\) qua đường thẳng \(EF\). Chứng minh rằng ba điểm \(A,\,\,T,\,\,K\) thẳng hàng

Lời giải:

a)

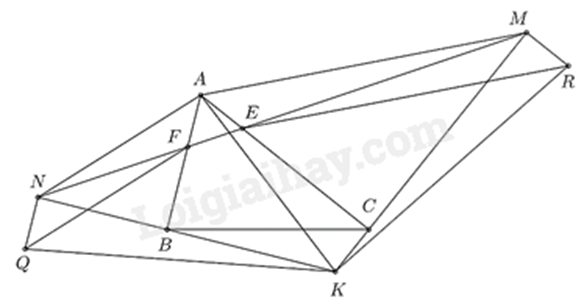
Vì tam giác \(AEF\) cân tại \(A\) (do \(AE = AF\)) nên \(\angle AEF = \angle AFE\)

Mà \(\angle MEC = \angle AEF,\,\,\angle NFB = \angle AFE\) nên \(\angle MEC = \angle NFB\)

Mặt khác \(\angle FNB = 90^\circ  - \angle NFB,\,\,\angle MEC = 90^\circ  - \angle CME\) nên \(\angle FNB = \angle CME\)

Hay \(\angle KNM = \angle KMN\)

Do đó tam giác \(KMN\) cân tại \(K\)

Vậy \(KM = KN\)

b) Vì \(ANQF\) là hình bình hành nên \(QN = AF\)

Vì \(AMRE\) là hình bình hành nên \(AE = MR\)

Mà \(AE = AF\) nên \(QN = MR\)

Vì \(ANQF\) là hình bình hành nên \(QN\parallel AF\)

Mà \(AF \bot NK\,\,\left( {gt} \right)\)nên \(QN \bot NK\)

Do đó \(\angle QNK = 90^\circ \)

Tương tư ta có \(\angle RMK = 90^\circ \)

Khi đó ta có \(\Delta KNQ = \Delta KMR\,\,\left( {c.g.c} \right)\)

Suy ra \(\angle NQK = \angle MRK\) (đpcm)

c)

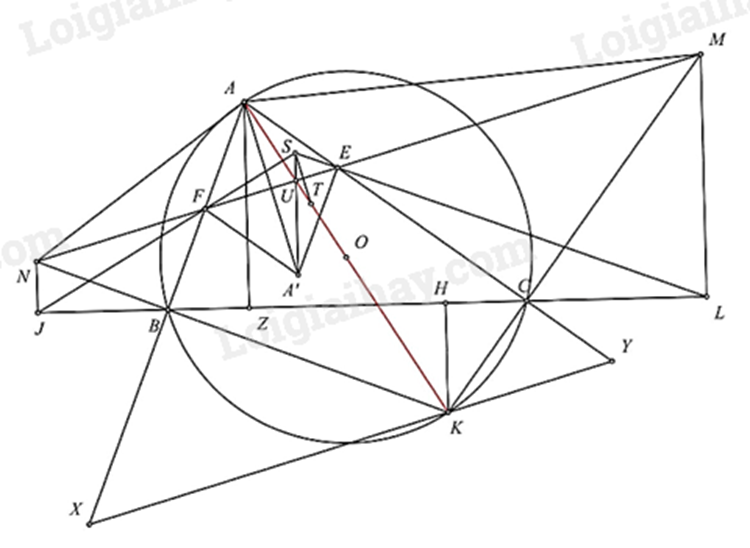
Trên cạnh \(EF\) lấy điểm \(U\) sao cho \(SU\) vuông góc với \(BC\)

Kẻ \(KH\) vuông góc với \(BC\)

Qua \(K\) kẻ đường thẳng song song với \(MN\) cắt \(AB,\,\,AC\) tương ứng tại \(X,\,\,Y\)

Áp dụng định lí Thales ta có: \(\frac{{NJ}}{{ML}} = \frac{{NJ}}{{SU}}.\frac{{SU}}{{ML}} = \frac{{NF}}{{FU}}.\frac{{EU}}{{EM}} = \frac{{NF}}{{EM}}.\frac{{EU}}{{FU}}\,\,\left( 1 \right)\)

Và \(\frac{{NJ}}{{ML}} = \frac{{NJ}}{{KH}}.\frac{{KH}}{{ML}} = \frac{{NB}}{{BK}}.\frac{{CK}}{{ML}} = \frac{{CK}}{{BK}}.\frac{{NB}}{{ML}}\,\,\left( 2 \right)\)

Xét \(\Delta NBF\) và \(\Delta MCE\) có

\(\begin{array}{l}\angle NBF = \angle MCE = 90^\circ \\\angle BNF = \angle CME\,\,\left( {cmt} \right)\end{array}\)

Suy ra \(\Delta NBF\backsim\Delta MCE\)

Do đó \(\frac{{NB}}{{ML}} = \frac{{NF}}{{EM}}\,\,\left( 3 \right)\)

Từ (1), (2) và (3) suy ra \(\frac{{EU}}{{FU}} = \frac{{CK}}{{BK}}\,\,\left( 4 \right)\)

Ta có: \(\angle KYC = \angle MEC = \angle AEF,\,\,\angle KXB = \angle NFB = \angle AFE\)

Suy ra \(\angle KYC = \angle KXB\)

Xét \(\Delta KYC\) và \(\Delta KXB\) có

\(\begin{array}{l}\angle KYC = \angle KXB\,\,\left( {cmt} \right)\\\angle KCY = \angle KBX = 90^\circ \end{array}\)

Do đó \(\Delta KYC\backsim \Delta KXB\,\,\left( g.g \right)\)

Suy ra \(\frac{{CK}}{{BK}} = \frac{{KY}}{{KX}}\,\,\left( 5 \right)\)

Từ (4) và (5) suy ra \(\frac{{EU}}{{FU}} = \frac{{KY}}{{KX}}\)

Do đó \(A,\,\,U,\,\,K\) thẳng hàng

Gọi \(A'\) đối xứng với \(A\) qua \(EF\)

Kẻ \(AZ\) vuông góc với \(BC\)

Ta có: \(\angle KAC + \angle AKC = 90^\circ ,\,\,\angle BAZ + \angle ABZ = 90^\circ ,\,\,\angle ABZ = \angle AKC\)

Do đó \(\angle BAZ = \angle CAK\)

Từ đó suy ra \(\angle ZAA' = \angle UAA'\)

Vì \(U\) thuộc \(EF\) nên \(UA = UA'\)

Do đó \(\angle UA'A = \angle UAA' = \angle ZAA'\)

Từ đó suy ra \(UA'\parallel AZ\)

Mà \(AZ \bot BC\) nên \(UA' \bot BC\)

Suy ra \(S,\,\,U,\,\,A'\) thẳng hàng

Từ đó ta có \(T,\,\,U,\,\,A\) thẳng hàng

Vậy \(T\) thuộc \(AK\)

Câu 4: (1 điểm) Tìm số nguyên dương \(k\) nhỏ nhất sao cho với mọi cách sắp xếp 99 điểm màu đỏ và 100 điểm màu xanh trên mặt phẳng (không có ba điểm nào thẳng hàng), ta luôn vẽ được \(k\) đường thẳng, mỗi đường thẳng không đi qua điểm nào trong các điểm trên và các đường thẳng đó chia mặt phẳng thành các miền mà trong mỗi miền không có hai điểm khác màu

Lời giải:

Xét đa giác lồi 199 đỉnh với 99 điểm tô màu đỏ và 99 điểm tô màu xanh xen kẽ nhau và 1 điểm màu xanh tùy ý trên 1 đường tròn

Đa giác có 198 cạnh chứa cả hai đỉnh màu xanh và màu đỏ

Rõ ràng 1 đường thẳng cắt nhiều nhất hai cạnh của đa giác trên và mỗi cạnh chứa cả hai đỉnh có 2 màu phải được cắt ít nhất bởi 1 đường thẳng nên số đường thẳng ít nhất là \(k \ge \frac{{198}}{2} = 99\)

Ta chứng minh \(k = 99\) thỏa mãn yêu cần của đề bài

Xét bao lồi \(S\) chứa các 199 điểm

Trường hợp 1: Nếu bao lồi có 1 điểm đỏ thì ta kẻ được một đường thẳng chia thành 2 miền đơn sắc (chỉ chứa màu đỏ hoặc màu xanh). Với 98 điểm đỏ còn lại, ta chia các điểm này thành 49 cặp, với 2 điểm \(A,\,\,B\) bất kì cùng màu ta kẻ hai đường thẳng song song với \(AB\) và cách \(AB\) một khoảng nhỏ để tạo ra một miền mới mà miền này chỉ chứa đúng hai điểm \(A,\,\,B\). Như vậy ta cần dùng \(1 + 49.2 = 99\) đường thẳng

Trường hợp 2: Nếu bao lồi gồm toàn các điểm xanh thì kẻ một đường thẳng song song, cách cạnh của bao lồi khoảng đủ nhỏ thì ta tách được hai điểm xanh ra một miền mới. Còn 98 điểm xanh, ta chia các điểm này thành 49 cặp, làm tương tự trường hợp trên ta sẽ kẻ được \(49.2 = 98\) đường thẳng. Như vậy ta cần kẻ 99 đường thẳng, mỗi điểm xanh chỉ nằm trong miền chứa toàn các điểm xanh khác.

Vậy \(\min k = 99\)