Đề thi vào 10 môn Toán Thái Bình năm 2025

Đề bài

Câu 1: (2 điểm) Cho hai biểu thức \(A = \frac{{6\sqrt x  - 8}}{{x - 16}} + \frac{{\sqrt x }}{{\sqrt x  + 4}} + \frac{2}{{\sqrt x  - 4}}\) và \(B = \frac{{x - \sqrt x  + 4}}{{\sqrt x  - 4}}\), với \(x \ge 0;x \ne 16\)

a) Tính giá trị của biểu thức \(B\) khi \(x = 9\).

b) Chứng minh rằng \(A = \frac{{\sqrt x }}{{\sqrt x  - 4}}\).

c) Đặt \({\rm{P}} = \frac{A}{B}\). Tìm giá trị lớn nhất của biểu thức \(P\).

Câu 2: (2,5 điểm)

a) Số bài tập về nhà môn Toán đã làm của 40 học sinh trong lớp 9A vào tuần trước được thống kê trong bảng tần số sau:

Lập bảng tần số tương đối của bảng số liệu trên.

b) Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số tự nhiên từ 1 đến 12, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một chiếc thẻ trong hộp. Tính xác suất của biến cố A: "Số xuất hiện trên thẻ được rút ra chia hết cho 3”

c) Một bình thủy tinh hình trụ đang chứa nước có bán kính đáy bên trong là \(R = 3\sqrt 2 \;{\rm{cm}}\) đặt trên mặt phẳng nằm ngang. Bạn Nam thả chìm hoàn toàn một viên bi sắt đặc dạng hình cầu có bán kính \(r = 3\;{\rm{cm}}\) vào trong bình thì thấy nước trong bình dâng lên \(x\;cm\,(x > 0)\) và không tràn ra ngoài. Tính thể tích của viên bi sắt và tìm giá trị của \(x\).

Câu 3: (2 điểm)

a) Trong thư viện có một giá sách được chia thành hai ngăn I và II. Ban đầu số cuốn sách ở ngăn I nhiều hơn số cuốn sách ở ngăn II là 100 cuốn. Sau khi người ta chuyển 25% số cuốn sách ở ngăn I sang ngăn II thì số cuốn sách ở ngăn I bằng 75% số cuốn sách ở ngăn II. Tính số cuốn sách ở mỗi ngăn lúc ban đầu.

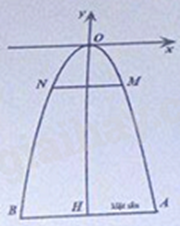
b) Ở một hội chợ thương mại, người ta dựng trên mặt sân một cái cổng có dạng parabol \(y = a{x^2}\)(như hình vẽ bên). Biết chiếc cổng có chiều cao OH = 8m, và khoảng cách giữa hai chân cổng là AB = 6m. Người ta treo trên cồng một dây đèn trang trí song song với đường thẳng AB, từ điểm M đến điểm N, khoảng cách MN = 3m. Tính giá trị của a và khoảng cách từ dây đèn đến mặt sân.

Câu 4: (3 điểm) Cho đường tròn \(\left( {O;R} \right)\) có hai đường kính AB và CD vuông góc với nhau. Lấy điểm M thuộc cung nhỏ BC (M khác B và M khác C). Đoạn thẳng MD cắt đoạn thẳng OB tại I, đoạn thẳng OC cắt đoạn thẳng AM tại K.

a) Chứng minh tứ giác OBMK nội tiếp.

b) Chứng minh rằng \(DI.DM = 2{R^2}\).

c) Tia phân giác của góc \(\angle IOM\) cắt MI tại điểm E. Chứng minh rằng \(\tan \angle ODI = \frac{{EI}}{{EM}}\)

d) Cho \(IB = 2.IO\). Tính tỉ số \(\frac{{MB}}{{MC}}\).

Câu 5: (0,5 điểm)  Cho \(a,b,c\) là các số không âm thoả mãn: \(a + b + c = 3\). Chứng minh rà̀ng:

\(\sqrt {6a + \frac{{{{(b - c)}^2}}}{2}}  + \sqrt {6b + \frac{{{{(c - a)}^2}}}{2}}  + \sqrt {6c + \frac{{{{(a - b)}^2}}}{2}}  \le 6\sqrt 2 .\)

-------- Hết --------

Lời giải

Câu 1. Cho hai biểu thức \(A = \frac{{6\sqrt x  - 8}}{{x - 16}} + \frac{{\sqrt x }}{{\sqrt x  + 4}} + \frac{2}{{\sqrt x  - 4}}\) và \(B = \frac{{x - \sqrt x  + 4}}{{\sqrt x  - 4}}\), với \(x \ge 0;x \ne 16\).

a) Tính giá trị của biểu thức B khi x = 9.

b) Chứng minh rằng \(A = \frac{{\sqrt x }}{{\sqrt x  - 4}}\).

c) Đặt \(P = \frac{A}{B}\). Tìm giá trị lớn nhất của biểu thức P.

Phương pháp:

a) Kiểm tra xem \(x = 9\) có thoả mãn điều kiện xác định hay không.

Nếu có, thay \(x = 9\) vào B để tính giá trị biểu thức.

b) Sử dụng cách biến đổi căn thức bậc hai để rút gọn biểu thức.

c) Rút gọn P, biến đổi để tìm giá trị nhỏ nhất của mẫu thức suy ra giá trị lớn nhất của biểu thức P.

Lời giải:

a) Với x = 9 (TMĐK) thay vào biểu thức B, ta có:

\(B = \frac{{9 - \sqrt 9  + 4}}{{\sqrt 9  - 4}} = \frac{{9 - 3 + 4}}{{3 - 4}} = \frac{{10}}{{ - 1}} =  - 10\)

Vậy \(B =  - 10\) khi \(x = 9\)

b) \(A = \frac{{6\sqrt x  - 8}}{{x - 16}} + \frac{{\sqrt x }}{{\sqrt x  + 4}} + \frac{2}{{\sqrt x  - 4}}\)

\(A = \frac{{6\sqrt x  - 8}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} + \frac{{\sqrt x \left( {\sqrt x  - 4} \right)}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} + \frac{{2\left( {\sqrt x  + 4} \right)}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}}\)

\(A = \frac{{6\sqrt x  - 8 + x - 4\sqrt x  + 2\sqrt x  + 8}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}}\)

\(A = \frac{{x + 4\sqrt x }}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} = \frac{{\sqrt x \left( {\sqrt x  + 4} \right)}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} = \frac{{\sqrt x }}{{\sqrt x  - 4}}\)

Vậy với \(x \ge 0;x \ne 16\) thì \(A = \frac{{\sqrt x }}{{\sqrt x  - 4}}\)

c) Với \(x \ge 0;x \ne 16\) thì \(x - \sqrt x  + 4 \ne 0\) và \(x \ge 0;x \ne 16\) nên \(B \ne 0\), ta có: \(P = \frac{A}{B} = \frac{{\sqrt x }}{{\sqrt x  - 4}}:\frac{{x - \sqrt x  + 4}}{{\sqrt x  - 4}} = \frac{{\sqrt x }}{{\sqrt x  - 4}} \cdot \frac{{\sqrt x  - 4}}{{x - \sqrt x  + 4}} = \frac{{\sqrt x }}{{x - \sqrt x  + 4}}\)

TH1: x = 0 suy ra P = 0

TH2: x ≠ 0, ta có: \(P = \frac{1}{{\frac{x}{{\sqrt x }} - 1 + \frac{4}{{\sqrt x }}}} = \frac{1}{{\sqrt x  - 1 + \frac{4}{{\sqrt x }}}} = \frac{1}{{\frac{{x - 4\sqrt x  + 4}}{{\sqrt x }} + 3}} = \frac{1}{{\frac{{{{\left( {\sqrt x  - 2} \right)}^2}}}{{\sqrt x }} + 3}}\)

Vì \({\left( {\sqrt x  - 2} \right)^2} \ge 0\) với mọi x nên \(\frac{{{{\left( {\sqrt x  - 2} \right)}^2}}}{{\sqrt x }} \ge 0\) với mọi x.

Suy ra \(P \le \frac{1}{3}\).

Dấu “=” xảy ra khi và chỉ khi \(\sqrt x  - 2 = 0\) hay \(\sqrt x  = 2\) hay \(x = 4\)(TMĐK)

Vậy giá trị lớn nhất của biểu thức P là: \(\frac{1}{3}\) khi \(x = 4\)

Câu 2.

a) Số bài tập về nhà môn Toán đã làm của 40 học sinh trong lớp 9A vào tuần trước được thống kê trong bảng tần số sau:

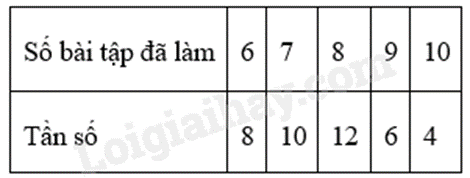
Lập bảng tần số tương đối của bảng số liệu trên.

b) Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số tự nhiên từ 1 đến 12, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một chiếc thẻ trong hộp. Tính xác suất của biến cố A: “Số xuất hiện trên thẻ được rút ra chia hết cho 3".

c) Một bình thủy tinh hình trụ đang chứa nước có bán kính đáy bên trong là \(R = 3\sqrt 2 \) cm đặt trên mặt phẳng nằm ngang. Bạn Nam thả chìm hoàn toàn một viên bi sắt đặc dạng hình cầu có bán kính \(r = 3\)cm vào trong bình thì thấy nước trong bình dâng lên x cm (x > 0) và không tràn ra ngoài. Tính thể tích của viên bi sắt và tìm giá trị của x.

Phương pháp:

a) Tính các tần số tương đối tương ứng, sau đó lập bảng tần số tương đối.

\({f_x} = \frac{m}{n}.100\% \) (m là tần số của x, n là cỡ mẫu).

b) Tính số kết quả có thể, số kết quả thuận lợi chon biến cố A.

Xác suất của biến cố A = số kết quả thuận lợi : số kết quả có thể.

c) Tính thể tích viên bi sắt.

Vì thể tích nước dâng lên bằng thể tích của viên bi nên ta giải phương trình để tìm x.

Lời giải:

a) Bảng tần số tương đối của bảng số liệu đã cho là:

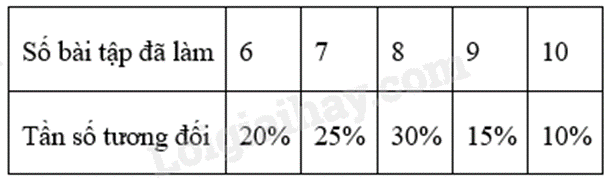
b) Không gian mẫu của phép thử là: \(\Omega  = \left\{ {1;2;3;...;11;12} \right\}\) có 12 phần tử.

Có 4 kết quả thuận lợi cho biến cố A là: 3; 6; 9; 12.

Xác suất của biến cố A là: \(P\left( A \right) = \frac{4}{{12}} = \frac{1}{3}\)

c) Thể tích của viên bi sắt là: \(V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {.3^3} = 36\pi \left( {c{m^3}} \right)\)

Vì thể tích nước dâng lên bằng thể tích của viên bi nên ta có

\(\pi {R^2}x = 36\pi \)

\(\pi .{\left( {3\sqrt 2 } \right)^2}.x = 36\pi \)

\(18\pi x = 36\pi \)

Suy ra: x = 2 (cm)

Câu 3.

a) Trong thư viện có một giá sách được chia thành hai ngăn I và II. Ban đầu số cuốn sách ở ngăn 1 nhiều hơn số cuốn sách ở ngăn II là 100 cuốn. Sau khi người ta chuyển 25% số cuốn sách ở ngăn I sang ngăn II thì số cuốn sách ở ngăn I bằng 75% số cuốn sách ở ngăn II. Tính số cuốn sách ở mỗi ngăn lúc ban đầu.

b) Ở một hội chợ thương mại, người ta dựng trên mặt sân một cái cổng có dạng parabol \(y = a{x^2}\) (như hình vẽ bên). Biết chiếc cổng có chiều cao OH = 8 m, và khoảng cách giữa hai chân cổng là AB = 6m. Người ta treo trên cổng một dây đèn trang trí song song với đường thẳng AB, từ điểm M đến điểm N, khoảng cách MN = 3 m. Tính giá trị của a và khoảng cách từ dây đèn đến mặt sân.

Phương pháp:

a) Gọi số cuốn sách ban đầu ở ngăn I là: x (cuốn) ĐK: x > 100 và \(x \in {N^{\rm{*}}}\).

Số cuốn sách ban đầu ở ngăn II là: y (cuốn) ĐK: \(y \in {N^{\rm{*}}}\).

Số cuốn sách ở ngăn 1 nhiều hơn số cuốn sách ở ngăn II là 100 cuốn nên ta có: \(y = x - 100\)

Sau khi chuyển, số cuốn sách ở ngăn I bằng 75% số cuốn sách ở ngăn II nên ta lập được phương trình.

Thế \(y = x - 100\) vào phương trình trên để tìm x.

Tìm giá trị \(y\) tương ứng.

b) Khoảng cách giữa hai chân cổng là: AB = 6m, suy ra AH = 3m.

Điểm A có hoành độ bằng 3, tung độ bằng - 8, A thuộc parabol nên ta giải tìm a.

Điểm N thuộc parabol nên ta tìm được toạ độ điểm N.

Suy ra khoảng cách từ dây đèn đến mặt sân.

Lời giải:

a) Gọi số cuốn sách ban đầu ở ngăn I là: x (cuốn) ĐK: x > 100 và \(x \in {N^{\rm{*}}}\).

Số cuốn sách ban đầu ở ngăn II là: y (cuốn) ĐK: \(y \in {N^{\rm{*}}}\).

Có y = x – 100.

Chuyển 25% số sách ngăn I sang ngăn II, khi đó số cuốn sách còn lại ở ngăn I là: x - 0,25x = 0,75x (Cuốn).

Số cuốn sách ở ngăn II là: y + 0,25x (cuốn).

Sau khi chuyển, số cuốn sách ở ngăn I bằng 75% số cuốn sách ở ngăn II, ta có phương trình: \(0,75x = 0,75.\left( {x--100 + 0,25x} \right)\) (1).

Thay y = x - 100 vào phương trình (1) ta có:

\(0,75x = 0,75.\left( {x--100 + 0,25x} \right)\)

\(0,75x = 0,9375x - 75\)

\(x = 400\)(TMĐK)

Suy ra: y = 400 – 100 = 300 (TMĐK)

Vậy số sách ban đầu ở ngăn I là 400 cuốn, số sách ban đầu ở ngăn II là 300 cuốn.

b) Khoảng cách giữa hai chân cổng là: AB = 6m, suy ra AH = 3m.

Điểm A có hoành độ bằng 3, tung độ bằng - 8, A thuộc parabol nên ta có: \( - 8 = a{.3^2}\)

suy ra: \(a = \frac{{ - 8}}{9}\)

Suy ra parabol: \(y = \frac{{ - 8}}{9}{x^2}\)

Có MN = 3m suy ra điểm N có hoành độ bằng – 1,5 và tung độ \({y_N}\)

Điểm N thuộc parabol nên ta có: \({y_N} = \frac{{ - 8}}{9}{\left( { - 1,5} \right)^2} =  - 2\)

Suy ra toạ độ của dây đèn thấp hơn chiếc cổng là 2m

Vậy khoảng cách từ dây đèn đến mặt sân là: 8 – 2 = 6 (m)

Câu 4. Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc với nhau. Lấy điểm M thuộc cung nhỏ BC (M khác B và M khác C). Đoạn thẳng MD cắt đoạn thẳng OB tại I, đoạn thẳng OC cắt đoạn thẳng AM tại K.

a) Chứng minh tứ giác OBMK nội tiếp.

b) Chứng minh rằng \(DI.DM = 2{R^2}\).

c) Tia phân giác của góc IOM cắt MI tại điểm E. Chứng minh rằng \(tanODI = \frac{{EI}}{{EM}}\)

d) Cho \(IB = 2.IO\). Tính tỉ số \(\frac{{MB}}{{MC}}\)

Phương pháp:

a) Chứng minh ΔKOB vuông tại O, ΔMKB vuông tại M nên M, K, B, O cùng thuộc đường tròn đường kính KB hay tứ giác OBMK nội tiếp.

b) Áp dụng tính chất góc nội tiếp chắn cung để tính \(\widehat {DMB}\) và \(\widehat {DBI}\), suy ra \(\widehat {DMB} = \widehat {DBI}\)

Chứng minh $\Delta DIB\backsim \Delta DBM\left( g-g \right)$ suy ra: \(DI.DM = D{B^2}\)

Áp dụng định lí Pythagore, chứng minh \(B{D^2} = 2{R^2}\)

Suy ra: \(DI.DM = 2{R^2}\)

c) Áp dụng tính chất đường phân giác, chứng minh \(\frac{{IE}}{{EM}} = \frac{{OI}}{{OM}}\)

Áp dụng tỉ số lượng giác, chứng minh \(tan\widehat {ODI} = \frac{{OI}}{{OD}}\) (6)

suy ra: \(tan\widehat {ODI} = \frac{{EI}}{{EM}}\)

d) Đặt IO = x thì IB = 2.IO = 2.x.

Tính \(DI\) và \(BD\) theo \(x\) và \(R\).

Chứng minh \(\frac{{DI}}{{DB}} = \frac{{IB}}{{MB}}\) suy ra \(MB\) theo \(x\) và \(R\).

Từ tỉ số lượng giác suy ra \(MC\) theo \(x\) và \(R\).

Suy ra tính \(\frac{{MB}}{{MC}}\).

Lời giải:

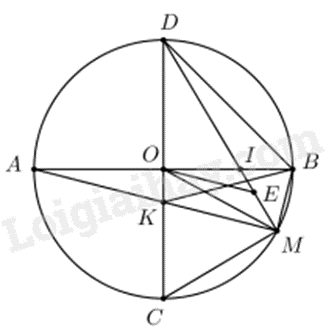
a) Do \(AB \bot C{\rm{D}}\) tại O nên ΔKOB vuông tại O hay O, K, B cùng thuộc đường tròn đường kính KB.

Có \(M \in \left( O \right)\) nên \(\angle AMB = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)

Khi đó ΔMKB vuông tại M nên M, K, B cùng thuộc đường tròn đường kính KB.

Vậy M, K, B, O cùng thuộc đường tròn đường kính KB hay tứ giác OBMK nội tiếp.

b) Ta có: $\widehat{DMB}=\frac{1}{2}sđ\overset\frown{BD}=\frac{1}{2}.90{}^\circ =45{}^\circ $ và $\widehat{DBI}=\frac{1}{2}sđ\overset\frown{AD}=\frac{1}{2}.90{}^\circ =45{}^\circ $

Nên \(\widehat {DMB} = \widehat {DBI}\left( { = 45^\circ } \right)\)

Xét \(\Delta DIB\) và \(\Delta DBM\) có \(\widehat {DMB} = \widehat {DBI}\) (cmt) và \(\widehat {MDB}\) chung

Suy ra: $\Delta DIB\backsim \Delta DBM\left( g-g \right)$ suy ra: \(\frac{{DI}}{{DB}} = \frac{{DB}}{{DM}}\) hay \(DI.DM = D{B^2}\) (3)

Có \(\Delta BOD\) vuông tại O (gt), theo định lí Pythagore ta có: \(B{D^2} = O{D^2} + O{B^2} = {R^2} + {R^2} = 2{R^2}\) (4)

Từ (3) và (4) suy ra: \(DI.DM = 2{R^2}\)

c) Do OE là tia phân giác của \(\widehat {MOI}\) nên \(\frac{{IE}}{{EM}} = \frac{{OI}}{{OM}}\) (tính chất đường phân giác) (5)

Mà \(\Delta OID\) vuông tại O nên \(tan\widehat {ODI} = \frac{{OI}}{{OD}}\) (6)

Từ (5) và (6) suy ra: \(tan\widehat {ODI} = \frac{{EI}}{{EM}}\)

d) Đặt IO = x thì IB = 2.IO = 2.x.

Khi đó \(DI = \sqrt {O{I^2} + O{D^2}}  = \sqrt {{x^2} + {R^2}} \) và \(BD = \sqrt {O{B^2} + O{D^2}}  = R\sqrt 2 \)

Theo b) ta có: $\Delta DIB\backsim \Delta DBM\left( g-g \right)$ nên \(\frac{{DI}}{{DB}} = \frac{{IB}}{{MB}}\)

Suy ra \(MB = \frac{{IB.DB}}{{DI}} = \frac{{2x.R\sqrt 2 }}{{\sqrt {{x^2} + {R^2}} }}\) (7)

Ta có: \(sin\widehat {IDO} = \frac{{OI}}{{DI}} = \frac{x}{{\sqrt {{x^2} + {R^2}} }}\) và \(sin\widehat {MDC} = \frac{{MC}}{{DC}} = \frac{{MC}}{{2R}}\)

Suy ra \(\frac{{MC}}{{2R}} = \frac{x}{{\sqrt {{x^2} + {R^2}} }}\)

Suy ra: \(MC = \frac{{2xR}}{{\sqrt {{x^2} + {R^2}} }}\) (8)

Từ (7) và (8) suy ra: \(\frac{{MB}}{{MC}} = \frac{{2x.R\sqrt 2 }}{{\sqrt {{x^2} + {R^2}} }}:\frac{{2xR}}{{\sqrt {{x^2} + {R^2}} }} = \frac{{2x.R\sqrt 2 }}{{2xR}} = \sqrt 2 \)

Câu 5. Cho a, b, c là các số không âm thoả mãn: a + b + c = 3. Chứng minh rằng:

\(\sqrt {6a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  + \sqrt {6b + \frac{{{{\left( {c - a} \right)}^2}}}{2}}  + \sqrt {6c + \frac{{{{\left( {a - b} \right)}^2}}}{2}}  \le 6\sqrt 2 \).

Phương pháp:

Thay 3 = a + b + c vào \(\sqrt {6a + \frac{{{{\left( {b - c} \right)}^2}}}{2}} \).

Sử dụng bất đẳng thức Cauchy, chứng minh \(\sqrt {6a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  \le \frac{{2a + b + c}}{{\sqrt 2 }}\).

Tương tự, \(\sqrt {6b + \frac{{{{\left( {c - a} \right)}^2}}}{2}}  \le \frac{{2b + a + c}}{{\sqrt 2 }}\) và \(\sqrt {6c + \frac{{{{\left( {a - b} \right)}^2}}}{2}}  \le \frac{{2c + a + b}}{{\sqrt 2 }}\).

Suy ra \(\sqrt {6a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  + \sqrt {6b + \frac{{{{\left( {c - a} \right)}^2}}}{2}}  + \sqrt {6c + \frac{{{{\left( {a - b} \right)}^2}}}{2}}  \le 6\sqrt 2 \).

Lời giải:

Ta có: \(\sqrt {6a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  + \sqrt {6b + \frac{{{{\left( {c - a} \right)}^2}}}{2}}  + \sqrt {6c + \frac{{{{\left( {a - b} \right)}^2}}}{2}}  \le 6\sqrt 2 \)

Đặt \(A = \sqrt {6a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  + \sqrt {6b + \frac{{{{\left( {c - a} \right)}^2}}}{2}}  + \sqrt {6c + \frac{{{{\left( {a - b} \right)}^2}}}{2}} \)

Vì a + b + c = 3 nên ta có:

\(\sqrt {6a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  = \sqrt {2.3.a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  = \sqrt {2.\left( {a + b + c} \right).a + \frac{{{{\left( {b - c} \right)}^2}}}{2}} \)

\( = \sqrt {2{a^2} + 2ab + 2ac + \frac{{{{\left( {b - c} \right)}^2}}}{2}} \)

\( = \sqrt {\frac{{4{a^2} + 4ab + 4ac + {{\left( {b - c} \right)}^2}}}{2}} \)

\( = \sqrt {\frac{{4{a^2} + 4a\left( {b + c} \right) + {{\left( {b + c} \right)}^2} - 4bc}}{2}} \)

\( = \sqrt {\frac{{{{\left( {2a + b + c} \right)}^2} - 4bc}}{2}}  = \sqrt {\frac{{{{\left( {2a + b + c} \right)}^2}}}{2} - 2bc} \)

\( \le \sqrt {\frac{{{{\left( {2a + b + c} \right)}^2}}}{2}}  = \frac{{2a + b + c}}{{\sqrt 2 }}\) (Vì a, b, c không âm)

Tương tự ta có: \(\sqrt {6b + \frac{{{{\left( {c - a} \right)}^2}}}{2}}  \le \frac{{2b + a + c}}{{\sqrt 2 }}\) và \(\sqrt {6c + \frac{{{{\left( {a - b} \right)}^2}}}{2}}  \le \frac{{2c + a + b}}{{\sqrt 2 }}\)

Khi đó: \(A \le \frac{{4a + 4b + 4c}}{{\sqrt 2 }} = \frac{{4.3}}{{\sqrt 2 }} = 6\sqrt 2 \)

 Dấu “=” xảy ra khi: a = b = 0; c = 3 hoặc b = c = 0 ; a = 3 hoặc a = c = 0; b = 3.